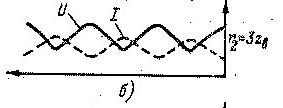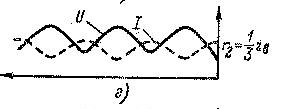Однородная линия без потерь. Уравнения линии без потерь

Независимо от того, соблюдается ли условие 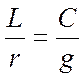(для неискаженной передачи требуется, чтобы коэффициент ослабления 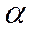не зависел от частоты, а коэффициент 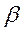был прямо пропорционален частоте; в последнем случае фазовая скорость 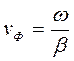получается не зависящей от частоты, такое положение имеет место при условии, что 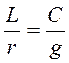.) или нет, во всех случаях желательно, чтобы активное сопротивление r и проводимость изоляции g были по возможности малы (для уменьшения потерь энергии).

В воздушных линиях обычно индуктивное сопротивление 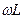превышает активное сопротивление r, а емкостная проводимость 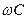превышает активную проводимость g. С ростом частоты разница между этими величинами становится более значительной.

В ряде случаев оказывается полезным в первом приближении рассматривать линию, не имеющую потерь, т.е. пренебрегать активным сопротивлением и проводимостью по сравнению с соответствующими реактивными составляющими. Такая идеализация допускается для приближенной качественной и количественной оценки исследуемых явлений. При этом весьма упрощаются расчетные выражения и гиперболические уравнения линии переходят в тригонометрические.

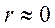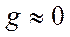Итак, основным исходным предложением, которое делают при рассмотрении линии без потерь, является приближенное условие, что и , в этом случае вторичные параметры линии примут весьма простой вид , а именно: ; ; ;

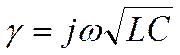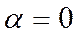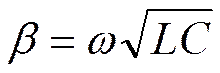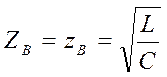
Следовательно в линии без потерь ослабление отсутствует. Ввиду постоянства фазовой скорости 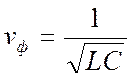отсутствуют также фазовые искажения.

Выражения для коэффициента фазы, фазовой скорости и волнового сопротивления линии без потерь совпадают с выражениями, полученными для линии без искажений (вопрос 57). Следовательно, все что сказано о линии без искажений, относится к линии без потерь.

Ввиду того что гиперболические функции с мнимым аргументом преобразуются в тригонометрические функции, гиперболические уравнения линии принимают тригонометрическую форму:

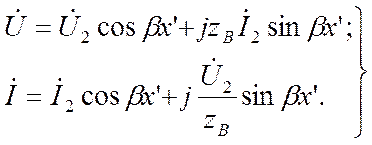
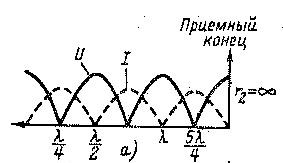
Эти уравнения используются для рассмотрения стоячих волн.

59. Линия без потерь. Уравнения линии. Построение распределения напряжений и токов вдоль линии при нагрузке Z_Н=3Z_В; 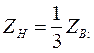Z_Н=Z_В.

Независимо от того, соблюдается ли условие 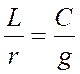(для неискаженной передачи требуется, чтобы коэффициент ослабления 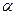не зависел от частоты, а коэффициент 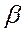был прямо пропорционален частоте; в последнем случае фазовая скорость 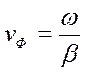получается не зависящей от частоты, такое положение имеет место при условии, что 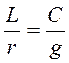.) или нет, во всех случаях желательно, чтобы активное сопротивление r и проводимость изоляции g были по возможности малы (для уменьшения потерь энергии).

В воздушных линиях обычно индуктивное сопротивление 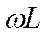превышает активное сопротивление r, а емкостная проводимость 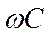превышает активную проводимость g. С ростом частоты разница между этими величинами становится более значительной.

В ряде случаев оказывается полезным в первом приближении рассматривать линию, не имеющую потерь, т.е. пренебрегать активным сопротивлением и проводимостью по сравнению с соответствующими реактивными составляющими. Такая идеализация допускается для приближенной качественной и количественной оценки исследуемых явлений. При этом весьма упрощаются расчетные выражения и гиперболические уравнения линии переходят в тригонометрические.

Итак, основным исходным предложением, которое делают при рассмотрении линии без потерь, является приближенное условие, что 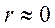и 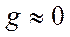, в этом случае вторичные параметры линии примут весьма простой вид , а именно: ; ; ;

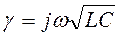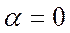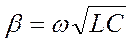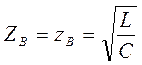
Следовательно в линии без потерь ослабление отсутствует. Ввиду постоянства фазовой скорости 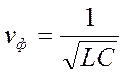отсутствуют также фазовые искажения.

Выражения для коэффициента фазы, фазовой скорости и волнового сопротивления линии без потерь совпадают с выражениями, полученными для линии без искажений (вопрос 57). Следовательно, все что сказано о линии без искажений, относится к линии без потерь.

Уравнения линии в показательной форме:

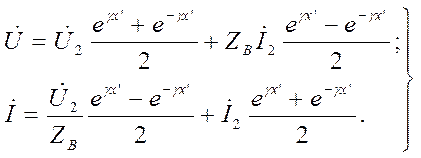
Уравнения линии в гиперболической форме:

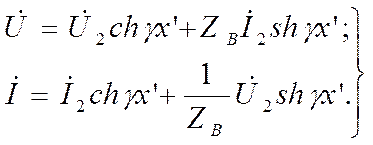
Положив в этих уравнениях, что 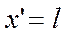, получим уравнения линии в гиперболической форме, выражающие напряжения и ток в начале через напряжения и ток в конце

:

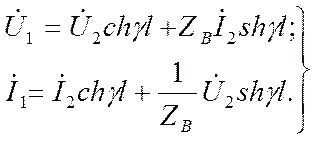
Ввиду того что гиперболические функции с мнимым аргументом преобразуются в тригонометрические функции, гиперболические уравнения линии принимают тригонометрическую форму: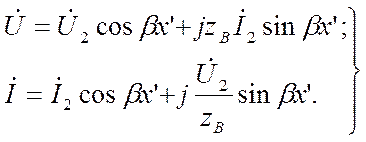

Последние уравнения используются для рассмотрения стоячих волн.

Построение распределения напряжений и токов вдоль линии при нагрузке Z_Н=3Z_В; 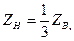Z_Н=Z_В.

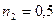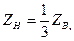
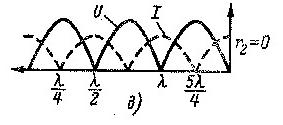
При активной нагрузке Z_Н=3Z_В , максимумы и минимумы U и I совпадают по своему местоположению с аналогичными значениями для режима холостого хода. При активной нагрузке 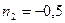Максимумы и минимумы расположены так же как и при коротком замыкании. При согласованной нагрузке Z_Н=Z_В. 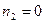, кривые U и I изображаются прямыми , параллельными оси абсцисс.