Как найти вектор по двум точкам?
Если даны две точки плоскости  и
и  , то вектор
, то вектор  имеет следующие координаты:
имеет следующие координаты:

Если даны две точки пространства  и
и  , то вектор
, то вектор  имеет следующие координаты:
имеет следующие координаты:

То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора.
Задание: Для тех же точек запишите формулы нахождения координат вектора  . Формулы в конце урока.
. Формулы в конце урока.
Пример 1
Даны две точки плоскости  и
и  . Найти координаты вектора
. Найти координаты вектора 
Решение: по соответствующей формуле:

Как вариант, можно было использовать следующую запись:

Эстеты решат и так: 
Лично я привык к первой версии записи.
Ответ: 
По условию не требовалось строить чертежа (что характерно для задач аналитической геометрии), но в целях пояснения некоторых моментов чайникам, не поленюсь:

Обязательно нужно понимать различие между координатами точек и координатами векторов:
Координаты точек – это обычные координаты в прямоугольной системе координат. Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.
Координаты же вектора – это его разложение по базису 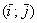 , в данном случае
, в данном случае  . Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости
. Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости 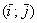 .
.
Записи координат точек и координат векторов вроде бы схожи:  , асмысл координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства.
, асмысл координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства.
Дамы и господа, набиваем руку:
Пример 2
а) Даны точки  и
и  . Найти векторы
. Найти векторы  и
и  .
.
б) Даны точки  и
и  . Найти векторы
. Найти векторы  и
и  .
.
в) Даны точки  и
и  . Найти векторы
. Найти векторы  и
и  .
.
г) Даны точки  . Найти векторы
. Найти векторы  .
.
Пожалуй, достаточно. Это примеры для самостоятельного решения, постарайтесь ими не пренебрегать, окупится ;-). Чертежи делать не нужно. Решения и ответы в конце урока.
Что важно при решении задач аналитической геометрии? Важно быть ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫМ, чтобы не допустить мастерскую ошибку «два плюс два равно нулю». Сразу извиняюсь, если где ошибся =)
Как найти длину отрезка?
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости  и
и  , то длину отрезка
, то длину отрезка  можно вычислить по формуле
можно вычислить по формуле 
Если даны две точки пространства  и
и  , то длину отрезка
, то длину отрезка  можно вычислить по формуле
можно вычислить по формуле 
Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты:  и
и  , но более стандартен первый вариант
, но более стандартен первый вариант
Пример 3
Даны точки  и
и  . Найти длину отрезка
. Найти длину отрезка  .
.
Решение: по соответствующей формуле:

Ответ: 
Для наглядности выполню чертёж

Отрезок  – это не вектор, и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ
– это не вектор, и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ  можно проверить обычной линейкой, непосредственно измерив длину отрезка.
можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Читаем!!!
Обратите внимание на важный технический приём – вынесение множителя из-под корня. В результате вычислений у нас получился результат  и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так:
и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так:  . Конечно, оставить ответ в виде
. Конечно, оставить ответ в виде  не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:

Нередко под корнем получается достаточно большое число, например  . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4:
. Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4:  . Да, разделилось нацело, таким образом:
. Да, разделилось нацело, таким образом:  . А может быть, число
. А может быть, число  ещё раз удастся разделить на 4?
ещё раз удастся разделить на 4?  . Таким образом:
. Таким образом:  . У числа
. У числа  последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять:
последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять:  . В результате:
. В результате:
 Готово.
Готово.
Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:

Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки  и
и  . Найти длину отрезка
. Найти длину отрезка  .
.
Решение и ответ в конце урока.
Как найти длину вектора?
Если дан вектор плоскости  , то его длина вычисляется по формуле
, то его длина вычисляется по формуле  .
.
Если дан вектор пространства  , то его длина вычисляется по формуле
, то его длина вычисляется по формуле  .
.
Данные формулы (как и формулы длины отрезка) легко выводятся с помощью небезызвестной теоремы Пифагора.
Пример 5
Даны точки  и
и  . Найти длину вектора
. Найти длину вектора  .
.
Я взял те же точки, что и в Примере 3.
Решение: Сначала найдём вектор  :
:

По формуле  вычислим длину вектора:
вычислим длину вектора:

Ответ: 
Не забываем указывать размерность – «единицы»! Всегда ли, кстати, нужно рассчитывать приближенное значение (в данном примере 8,94), если этого не требуется в условии? С моей точки зрения, лишним не будет, отсутствие приближенного значения тянет на придирку. Округление целесообразно проводить до 2-3 знаков после запятой.
Выполним чертеж к задаче:

В чём принципиальное отличие от Примера 3? Отличие состоит в том, что здесь речь идёт о векторе, а не об отрезке. Вектор можно переместить в любую точку плоскости.
А в чём сходство Примера 3 и Примера 5? Геометрически очевидно, что длина отрезка  равна длине вектора
равна длине вектора  . Так же очевидно, что длина вектора
. Так же очевидно, что длина вектора  будет такой же. По итогу:
будет такой же. По итогу: 
Задачу 3 можно было решить и вторым способом, повторю условие: Даны точки  и
и  . Найти длину отрезка
. Найти длину отрезка  .
.
Вместо применения формулы  , поступаем так:
, поступаем так:
1) Находим вектор  .
.
2) А теперь ссылаемся на то, что длина отрезка  равна длине вектора
равна длине вектора  :
:

Этот способ широко практикуется в ходе решений задач аналитической геометрии.
Вышесказанное справедливо и для пространственного случая
Для тренировки:
Пример 6
а) Даны точки  и
и  . Найти длину вектора
. Найти длину вектора  .
.
б) Даны векторы  ,
,  ,
,  и
и  . Найти их длины.
. Найти их длины.
Решения и ответы в конце урока.
