Баланс мощностей в сложной цепи
Сумма комплексных мощностей всех источников энергии в сколь угодно сложной электрической цепи равна сумме комплексных мощностей приемников в этой цепи
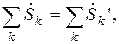 или
или 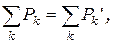
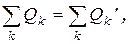
где 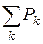 и
и 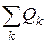 - сумма активных и сумма реактивных мощностей всех источников энергии в цепи, а
- сумма активных и сумма реактивных мощностей всех источников энергии в цепи, а 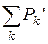 и
и 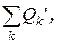 - сумма активных и сумма реактивных мощностей всех приемников.
- сумма активных и сумма реактивных мощностей всех приемников.
Последние два соотношения представляют собой уравнения баланса активных и реактивных мощностей в цепи.
Для источников э.д.с. 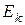 и тока
и тока 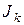 справедливы равенства
справедливы равенства
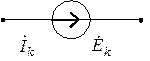 | 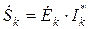 | 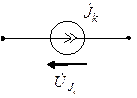 | 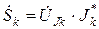 |
а для любого приемника можно записать
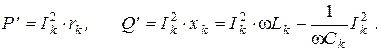
В качестве примера проверим выполнение условия баланса активных и реактивных мощностей в предыдущей задаче.
Комплексная мощность источника э.д.с. равна
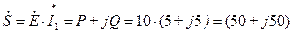 ВА,
ВА,
откуда имеем
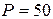 Вт,
Вт, 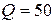 вар.
вар.
Активная мощность выделяется в активном сопротивлении 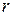 цепи
цепи
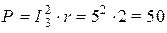 Вт.
Вт.
Реактивная мощность приемника равна
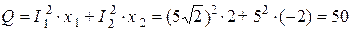 вар.
вар.
Данные расчета свидетельствуют о выполнении условия баланса мощностей.
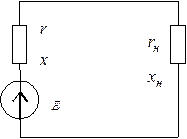 Рассмотрим вопрос об определении активной мощности в нагрузке, подсоединенной к источнику синусоидальной э.д.с. с действующим значением э.д.с.
Рассмотрим вопрос об определении активной мощности в нагрузке, подсоединенной к источнику синусоидальной э.д.с. с действующим значением э.д.с. 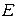 и внутренним сопротивлением
и внутренним сопротивлением 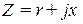 . Определим сопротивление
. Определим сопротивление 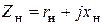 нагрузки таким образом, чтобы выделяемая в ней активная мощность
нагрузки таким образом, чтобы выделяемая в ней активная мощность 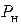 была максимальной.
была максимальной.
Активная мощность, выделяемая в нагрузке, равна
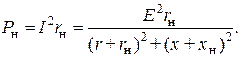
Очевидно, что для получения наибольшей мощности 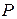 реактивное сопротивление нагрузки должно иметь значение
реактивное сопротивление нагрузки должно иметь значение 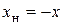 . Тогда максимум отдаваемой в нагрузку мощности можно определить из условия
. Тогда максимум отдаваемой в нагрузку мощности можно определить из условия
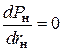 ,
,
откуда следует, что 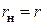 .
.
Таким образом, условия согласования нагрузки и источника, обеспечивающие максимальную мощность в приемнике, имеют вид:
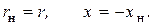
При этом потери 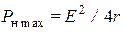 в активном сопротивлении нагрузки равны потерям
в активном сопротивлении нагрузки равны потерям 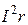 во внутреннем сопротивлении источника, составляя половину отдаваемой источником активной мощности. Поэтому к.п.д., определяемый как отношение потребляемой в нагрузке мощности, к мощности, вырабатываемой источником, будет равен 0,5, а напряжение на нагрузке составит половину напряжения источника.
во внутреннем сопротивлении источника, составляя половину отдаваемой источником активной мощности. Поэтому к.п.д., определяемый как отношение потребляемой в нагрузке мощности, к мощности, вырабатываемой источником, будет равен 0,5, а напряжение на нагрузке составит половину напряжения источника.
В электроэнергетических установках режим передачи максимальной мощности невыгоден вследствие значительных потерь энергии в проводах линии, соединяющих генераторы и потребителей. На практике силовые установки проектируют так, чтобы к.п.д. составлял 0,9-0,95, а напряжение на нагрузке отличалось бы от напряжения холостого хода не более, чем на 5-10 процентов.
В устройствах автоматики, связи, в электронных приборах мощности сигналов весьма малы, поэтому зачастую приходится создавать условия для передачи приемнику максимальной мощности. Снижение к.п.д. при этом не имеет существенного значения, так как передаваемая мощность невелика.
Для лучшего усвоения изложенного материала рассмотрим решение нескольких задач.
Задача 1. Для цепи, схема которой изображена на рисунке, определить следующие величины: эквивалентное комплексное сопротивление 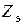 , эквивалентные активное
, эквивалентные активное 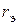 и реактивное
и реактивное 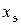 сопротивления, угол
сопротивления, угол 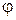 сдвига тока по отношению к напряжению, эквивалентные комплексную
сдвига тока по отношению к напряжению, эквивалентные комплексную 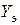 , активную
, активную 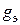 и реактивную
и реактивную 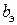 проводимости. Значения сопротивлений элементов при частоте
проводимости. Значения сопротивлений элементов при частоте 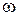 синусоидального напряжения источника составляют
синусоидального напряжения источника составляют 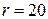 Ом ,
Ом , 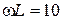 Ом ,
Ом , 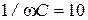 Ом .
Ом .
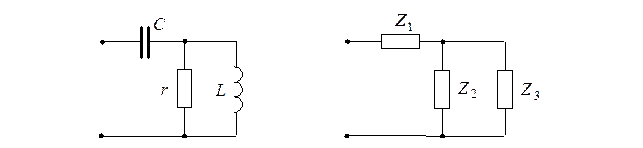
Решение Комплексные сопротивления ветвей схемы имеют вид
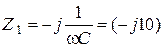 Ом,
Ом, 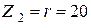 Ом,
Ом, 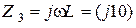 Ом.
Ом.
Эквивалентное комплексное сопротивление цепи определим из соотношения
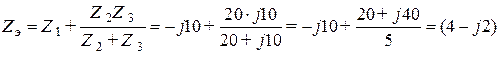 Ом.
Ом.
Поскольку 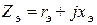 , можно записать
, можно записать 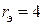 Ом,
Ом, 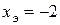 Ом.
Ом.
Угол сдвига  между током и напряжением
между током и напряжением
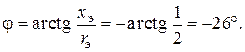
Для определения эквивалентных проводимостей воспользуемся соотношением
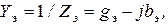
откуда имеем 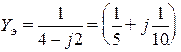 См ,
См , 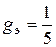 См ,
См , 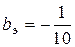 См .
См .
Найденные значения эквивалентных параметров цепи 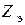 и
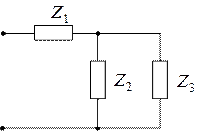
и 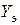 позволяют построить эквивалентные схемы замещения рассматриваемой цепи
позволяют построить эквивалентные схемы замещения рассматриваемой цепи
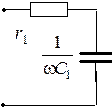 | 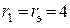 Ом, Ом,  | 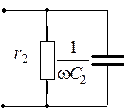 | 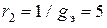 Ом , Ом , 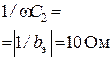 |
Задача 2. В цепи, изображенной на рисунке, известен ток во второй ветви 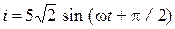 и параметры элементов цепи на частоте
и параметры элементов цепи на частоте 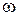 :
: 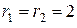 Ом,
Ом, 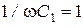 Ом,
Ом, 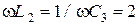 Ом. Рассчитать мгновенные значения напряжения и тока на входе цепи. Проверить условие баланса активной и реактивной мощностей.
Ом. Рассчитать мгновенные значения напряжения и тока на входе цепи. Проверить условие баланса активной и реактивной мощностей.
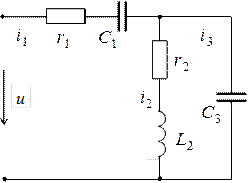
Решение. Рассчитаем комплексные сопротивления ветвей схемы.
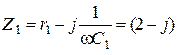 Ом,
Ом, 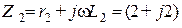 Ом,
Ом, 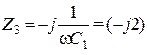 Ом.
Ом.
Комплексное изображение тока второй ветви 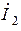 имеет вид:
имеет вид:
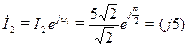 А.
А.
Поскольку вторая и третья ветви схемы соединены параллельно, то можно записать
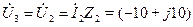 В.
В.
Тогда для тока 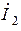 получим
получим 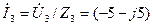 А.
А.
Для определения тока в первой ветви воспользуемся первым законом Кирхгофа
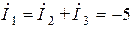 А.
А.
При известном токе 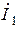 легко определяется напряжение на зажимах первой ветви
легко определяется напряжение на зажимах первой ветви
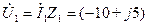 В.
В.
Согласно второму закону Кирхгофа входное напряжение 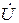 будет равно
будет равно
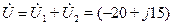 В.
В.
Для расчета мгновенных значений тока и напряжения на входе цепи запишем соответствующие комплексные переменные в показательной форме 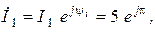 где
где 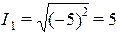 А,
А, 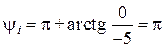 ;
;
Аналогично 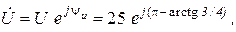
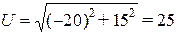 В,
В, 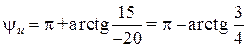 .
.
Окончательно получим:
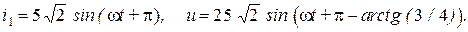
Комплексная мощность, создаваемая источником, может быть найдена из соотношения
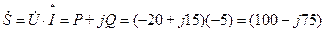 ВА,
ВА,
откуда активная мощность, отдаваемая источником, 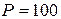 Вт, а реактивная мощность
Вт, а реактивная мощность 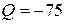 вар.
вар.
Активная мощность, потребляемая в цепи, выделяется на резисторах с сопротивлениями 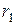 и
и 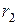 . Следовательно,
. Следовательно,
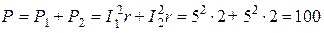 Вт.
Вт.
Реактивная мощность приемника определится в виде
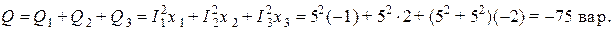
Выполнение баланса активных и реактивных мощностей свидетельствует о правильности выполнения расчетов.
Задача 3. Рассчитать сложную электрическую цепь, схема которой изображена на рисунке. Определить токи в ветвях методом контурных токов и методом узловых напряжений, а также ток пятой ветви методом эквивалентного генератора. Проверить условие выполнения в цепи баланса активной и реактивной мощностей. Сопротивления всех элементов цепи на частоте 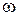 равны 1 Ом,
равны 1 Ом, 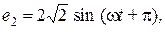
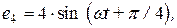
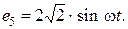
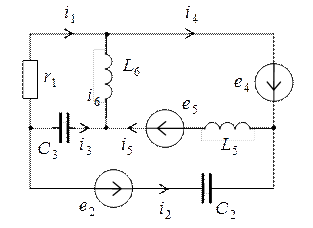
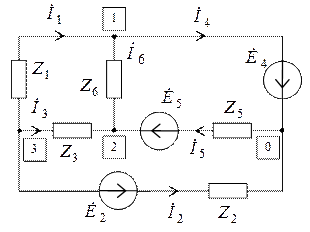
Решение Схема цепи для расчета комплексных токов содержит комплексные сопротивления ветвей и комплексные источники э.д.с., принимающие в данной задаче значения
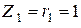 Ом,
Ом, 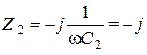 Ом,
Ом, 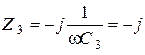 Ом,
Ом, 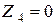 ,
, 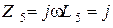 Ом,
Ом, 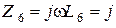 Ом,
Ом, 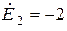 В,
В, 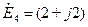 В,
В, 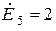 В.
В.
Метод контурных токов Определим порядок 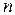 системы уравнений, которую следует записать согласно методу контурных токов. Для данной схемы число ветвей
системы уравнений, которую следует записать согласно методу контурных токов. Для данной схемы число ветвей 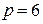 , число узлов
, число узлов 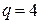 , поэтому
, поэтому 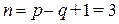 .
.
Система уравнений метода контурных токов имеет вид
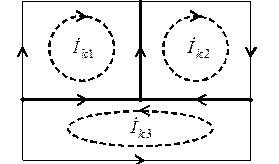
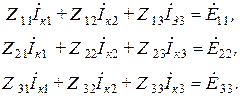
Выберем независимые контуры, изобразив граф схемы, в котором ветви 3,5,6 составляют дерево графа, а ветви 1,2,4 являются связями.
Собственные сопротивления контуров определяются из соотношений:
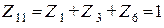 Ом,
Ом, 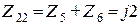 Ом,
Ом, 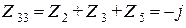 Ом.
Ом.
Сопротивления ветвей, общих для пары контуров, равны
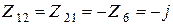 Ом,
Ом, 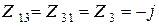 Ом,
Ом, 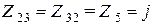 Ом.
Ом.
Контурные э.д.с. принимают значения
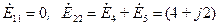 В,
В, 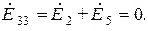
Таким образом исходная система уравнений примет вид
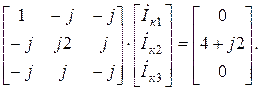
В результате решения этой системы значения контурных токов будут равны
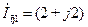 А,
А, 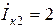 А,
А, 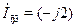 А,
А,
тогда комплексные токи в ветвях определятся следующим образом
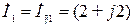 А,
А, 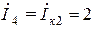 А,
А,
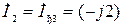 А,
А, 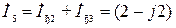 А,
А,
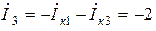 А,
А, 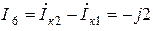 А .
А .
Мгновенные значения токов ветвей равны
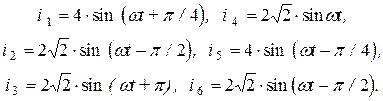
Метод узловых напряжений Порядок системы уравнений, составленной по методу узловых напряжений, равен 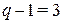 , а сами уравнения имеют вид
, а сами уравнения имеют вид
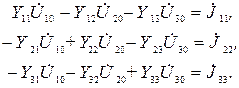
В качестве опорного узла выберем один из узлов, к которым подходит ветвь с идеальным источником э.д.с., остальные узлы нумеруем произвольно. В результате узловое напряжение 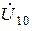 определится как
определится как
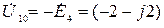 В,
В,
следовательно, первое уравнение может быть исключено из системы уравнений, что приводит к соотношениям
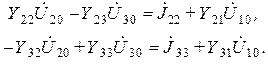
Рассчитаем значения собственных проводимостей узлов
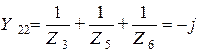 См,
См, 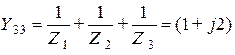 См.
См.
Проводимости между узлами равны
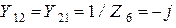 См,
См, 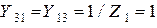 См,
См,
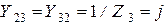 См.
См.
Задающие токи, подходящие к узлам, определим из соотношений
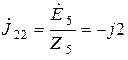 А,
А, 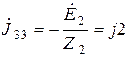 А.
А.
После подстановки найденных значений коэффициентов и правых частей уравнений, получим
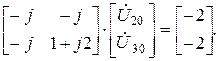
Решение этой системы уравнений имеет вид
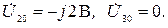
Токи в ветвях определим из соотношений, записанных согласно второму закону Кирхгофа для каждой ветви
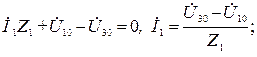
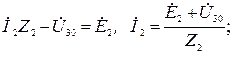
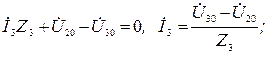
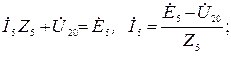
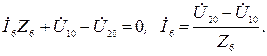
Ток ветви с идеальным источником э.д.с. равен
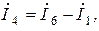
что следует из уравнения, составленного по первому закону Кирхгофа для первого узла.
Нетрудно убедиться, что значения найденных таким образом токов, совпадают с результатами, полученными методом контурных токов.
Метод эквивалентного генератора Рассчитаем ток в пятой ветви методом эквивалентного генератора, согласно которому
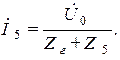
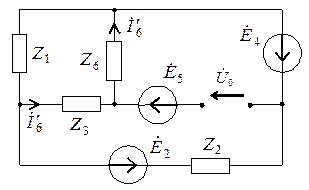 Для определения напряжения
Для определения напряжения 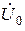 , возникающего при размыкании пятой ветви, составим уравнение по второму закону Кирхгофа
, возникающего при размыкании пятой ветви, составим уравнение по второму закону Кирхгофа
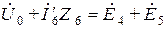
При определении тока 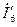 заметим, что в данной схеме
заметим, что в данной схеме
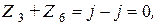 и
и 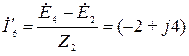 А.
А.
Следовательно,
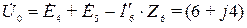 В.
В.
Для определения 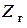 необходимо рассчитать эквивалентное сопротивление цепи относительно зажимов пятой ветви (узлы 0 и 2 на исходной схеме), замкнув накоротко источники э.д.с. При этом схема примет вид представленный на следующем рисунке.
необходимо рассчитать эквивалентное сопротивление цепи относительно зажимов пятой ветви (узлы 0 и 2 на исходной схеме), замкнув накоротко источники э.д.с. При этом схема примет вид представленный на следующем рисунке.
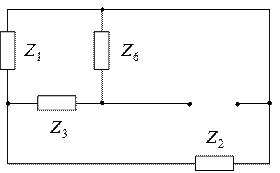
и искомое сопротивление определится соотношением
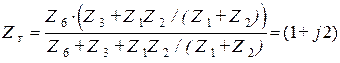 Ом.
Ом.
В результате значение тока в пятой ветви становится равным
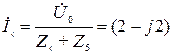 А,
А,
что совпадает с результатом, полученным ранее другими методами.
Расчет активной и реактивной мощности Комплексная мощность, создаваемая источниками, равна в данной цепи сумме комплексных мощностей всех источников э.д.с.
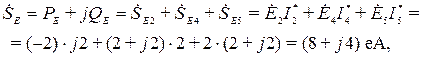
откуда 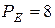 Вт,
Вт, 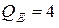 вар.
вар.
Активная мощность потребляется только в первой ветви с сопротивлением 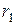
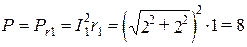 Вт.
Вт.
Реактивные мощности ветвей определим из соотношений
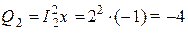 вар,
вар, 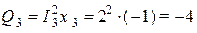 вар,
вар,
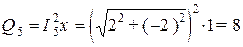 вар,
вар, 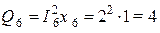 вар,
вар,
тогда суммарная реактивная мощность 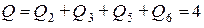 вар.
вар.
Ввиду выполнения равенств 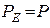 и
и 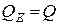 баланс мощности выполняется.
баланс мощности выполняется.
