Алгебраические критерии устойчивости

Использование этих критериев позволяет проверить устойчивость системы, не прибегая к решению характеристического уравнения и графическим построениям, ограничиваясь лишь алгебраическими вычислениями над коэффициентами характеристического уравнения.

Критерий устойчивости Рауса.

Критерий, сформулированный английским математиком Раусом в 1875 г (1877 г) представляет собой правило, определяющее ряд последовательных алгебраических операций, необходимых для решения задачи поверки устойчивости системы.

Допустим, что характеристическое уравнение исследуемой системы будет

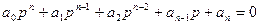(5-4)

Раус предложил использовать схему составления таблицы в виде таблицы коэффициентов. Таблица 5.1

Таблица коэффициентов.

№ строки	№ столбца
	…	…	…	…

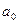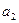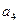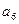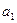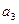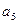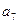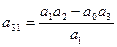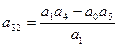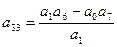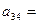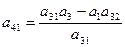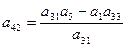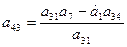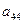Метод составления таблицы:

Первая строка - составляется из коэффициентов характеристического уравнения с четными индексами, начиная с .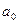

Вторая строка – из коэффициентов с нечетными индексами

Третья строка получается перекрестным умножением соответствующих коэффициентов первых двух строк делением на элемент первого столбца предыдущей строки.

Все последующие строки получают аналогичным способом из двух предыдущих строк

После построения приведенной выше таблицы критерий Рауса может быть сформулирован следующим образом. Для того чтобы АСР была устойчива, необходимо и достаточно, чтобы все элементы первого столбца таблицы, составленные из коэффициентов характеристического уравнения системы, были отличны от нуля и положительны при условии, что коэффициент 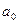при старшем члене уравнения больше нуля. Критерий Рауса особенно удобен в тех случаях, когда коэффициенты характеристического уравнения заданы численно.

Критерий Гурвица.Иная форма критерия устойчивости, наиболее распространенная в технической литературе, известна под названием критерия Гурвица, который сформулирован швейцарским ученным Гурвицем в 1895г. Последний основан на построении специальных определителей характеристического уравнения, называемых определителями или матрицами Гурвица.

Пусть дано характеристическое уравнение замкнутой системы, с постоянными коэффициентами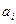

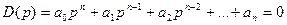, (5-5)

у которого коэффициент при старшем члене .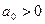

Определители Гурвица будут:

; ; ,…

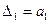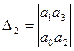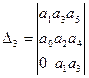и в общем виде

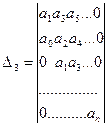, матрица размером n×n-матрица Гурвица.

При составлении определителя (матрицы) Гурвица n-го порядка руководствуются следующим правилом:

1) выписывают по главной диагонали все коэффициенты от 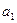до 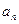в порядке возрастания индексов;

2) дополняют все столбцы определителя вверх от диагонали коэффициентами, с последовательно возрастающими, а вниз с последовательно убывающими индексами;

3) наибольший порядок определителя Гурвица равен степени характеристического уравнения;

4) на место коэффициентов, индексы которых больше n и меньше нуля, ставятся нули.

5) Последний определитель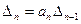

Критерий Гурвица формируется следующим образом: для того чтобы САР была устойчива, необходимо и достаточно, чтобы все определители 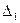, , 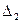…, , 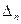составленные по коэффициентам характеристического уравнения системы до 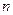-го порядка включительно, были положительны, при этом должно быть .

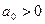При соблюдении критерия положительности коэффициентов характеристического уравнения проверка последнего определителя Гурвица 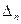необязательна т.к. при 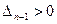всегда следует, что .

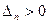Алгебраические критерии дают весьма простой способ исследования устойчивости систем в тех случаях, когда степень характеристического уравнения высока (например, n>5) и коэффициенты его заданы численно.

Для систем, характеристические уравнения которых имеют низкую степень (n≤4), условия устойчивости можно записать в общей форме в виде простых буквенных неравенств.

Условия устойчивости для систем с характеристическим уравнениями 2-ой, 3-ей и 4-ой степеней, вытекающие из критериев Рауса и Гурвица.

, ; ; .

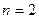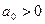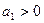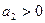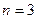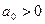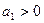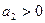, ; ; - основное неравенство,

дополнительное неравенство .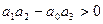

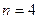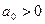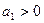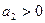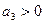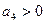, ; ; ; ; - основное неравенство

дополнительное неравенство

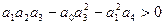
При 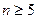число подобных дополнительных неравенств возрастает.

Если приравнять 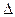n к нулю, то получим уравнение границ устойчивости

;

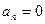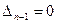
Первая граница 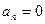соответствует наличию у характеристического уравнения нулевого корня ( 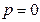). Вторая граница 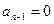соответствует наличию у характеристического уравнения чисто мнимых корней ( ).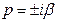