БИЛЕТ №7

Закон Джоуля-Ленца в интегральной форме. Работа А при перемещении заряда q из точки 1 в точку 2 равна

.

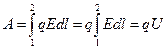Мощность

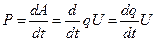, Þ

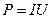. (47)

Если на участке нет эдс, и вся работа тока идет на нагревание, то за время dt в проводнике выделится количество теплоты 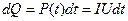. Поскольку 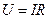, Þ 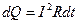. Интегрируя, получим закон Джоуля-Ленца в интегральной форме:

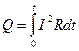. (48)

Если ток – постоянный, то выражение упрощается: .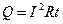

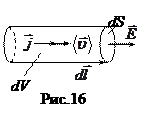Закон Джоуля-Ленца в дифференциальной форме. Вычислим энергию, которая выделяется в малом объеме проводника dV (рис.16), предполагая для простоты, что векторы плотности тока и напряженности поля сонаправлены, а вектор 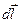выбран в том же направлении: ↑↑ ↑↑ 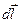. При перемещении заряда dq на 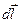поле совершает работу 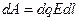. Подставим 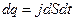и напряженность из закона Ома 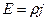, тогда эта работа равна

.

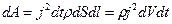Считая, что вся эта работа идет на нагревание ( 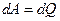), получим

,

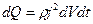где 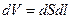. Тогда теплота, выделяющаяся в единице объема проводника в единицу времени, равна

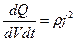. (49)

Величина слева называется удельной тепловой мощностью тока, а сам Закон Джоуля-Ленца в дифференциальной форме утверждает: удельная тепловая мощность тока пропорциональна квадрату плотности тока в той же точке.