Свойства математического ожидания дискретной случайной величины
1. Математическое ожидание постоянной величины 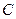 равно самой этой величине: если
равно самой этой величине: если 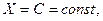 то
то 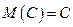 .
.
Закон распределения:
| X | C | C | C | … | C |
| P | p1 | p2 | p3 | … | pк |
Это непосредственно следует из определения 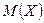 . Так как
. Так как 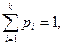
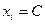 , т.е. случайная величина принимает единственное значение
, т.е. случайная величина принимает единственное значение 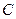 с вероятностью 1, то
с вероятностью 1, то
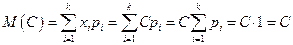 ,
,
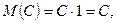
что и требовалось доказать.
2. Постоянный множитель можно выносить за знак математического ожидания:
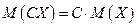 .
.
Закон распределения случайной величины 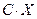 имеет вид:
имеет вид:
| CX | Cx1 | Cx2 | Cx3 | … | Cxк |
| P | p1 | p2 | p3 | … | pк |
Тогда
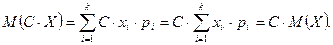
3. Математическое ожидание д.с.в. заключено между ее наименьшим и наибольшим значениями: если 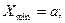
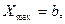 тo
тo
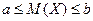 .
.
4. Математическое ожидание алгебраической суммы случайных величин равно алгебраической сумме математических ожиданий этих величин:
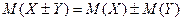 .
.
5. Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий этих величин: если  и
и 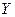 – независимые случайные величины, то
– независимые случайные величины, то
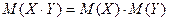 .
.
Дисперсия дискретной случайной величины. 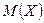 не даётполной характеристики закона распределения д.с.в. На практике часто приходится оценивать рассеивание возможных значений д.с.в. вокруг ее среднего значения.
не даётполной характеристики закона распределения д.с.в. На практике часто приходится оценивать рассеивание возможных значений д.с.в. вокруг ее среднего значения.
Так, при одинаковой средней величине годовых осадков одна местность засушлива и неблагоприятна для с.-х. работ, так как нет дождей весной и летом, а другая благоприятна для ведения с.-х. Поэтому необходимо введение новой числовой характеристики, по которой можно судить о рассеянии возможных значений этой случайной величины.
Пример 13.6. Пусть две случайные величины  и
и 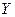 распределены по следующим законам:
распределены по следующим законам:
| Х | -10 | -6 | -2 | |||||
| Р | 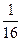 | 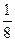 | 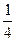 | 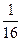 | 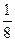 | 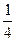 | 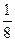 | 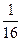 |
| Y | -2 | -1 | ||||||
| Р | 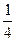 | 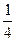 | 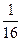 | 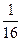 | 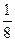 | 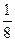 | 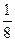 |
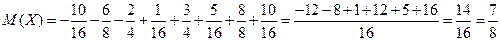 .
.
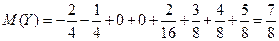 .
.
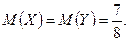
Изобразим значения этих величин геометрически (рис. 13.4).
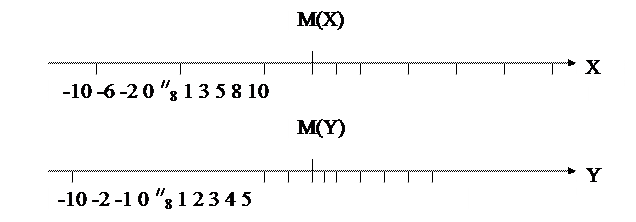 |
Рис. 13.4
Различие случайных величин Х и Y, имеющих одинаковые математические ожидания, состоит в неодинаковом разбросе значений случайной величины около ее математического ожидания. Характер этого разброса является важной информацией о случайной величине: чем меньше этот разброс, тем теснее арифметические средние 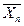 возможных значений случайной величины сосредотачиваются около математического ожидания М(Х).
возможных значений случайной величины сосредотачиваются около математического ожидания М(Х).
Удобной мерой разброса значений случайной величины  оказалось математическое ожидание случайной величины
оказалось математическое ожидание случайной величины 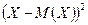 , представляющей квадрат отклонения случайной величины Х от её среднего значения
, представляющей квадрат отклонения случайной величины Х от её среднего значения 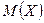 , т.е. величина
, т.е. величина 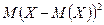 .
.
Определение 13.14. Отклонением случайной величины  от ее математического ожидания
от ее математического ожидания 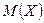 называют случайную величину
называют случайную величину 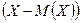 .
.
Закон распределения случайной величины 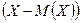 имеет вид:
имеет вид:
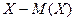 | 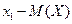 | …… | 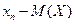 |
| P | p1 | …… | pn |
На первый взгляд кажется, что для оценки рассеяния значений д.с.в. проще вычислить все возможные значения отклонения д.с.в. и затем найти их среднее. Но это ничего не даст, так как 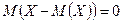 .
.
Теорема 13.2.Математическое ожидание отклонения случайной величины  от ее математического ожидания равно нулю:
от ее математического ожидания равно нулю:
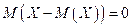 .
.
Доказательство. В самом деле,
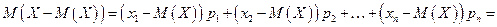
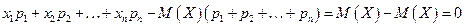 .
.
Определение 13.15. Дисперсией 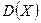 случайной величины
случайной величины  называется математическое ожидание квадрата отклонения случайной величины
называется математическое ожидание квадрата отклонения случайной величины 
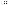 от ее математического ожидания
от ее математического ожидания 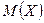 :
:
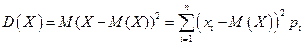 ,
,
т.е.
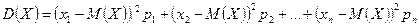 .
.
Закон распределения случайной величины 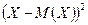 имеет вид:
имеет вид:
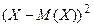 | 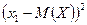 | 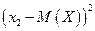 | …… | 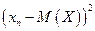 |
| P | p1 | p2 | …… | pn |
Дисперсия является мерой рассеивания случайной величины. Из двух случайных величин, описывающих результаты измерений одного и того же объекта с равными математическими ожиданиями, та считается лучшей, которая имеет меньший разброс значений, т.е. меньшую дисперсию.
Пример 13.7. Для случайных величин  и
и 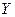 заданных в примере 13.1, дисперсии равны
заданных в примере 13.1, дисперсии равны
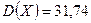 и
и 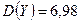 .
.
Оказалось, что значения 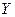 лучше соответствуют свойствам измеряемого объекта. Если применить формулу алгебры
лучше соответствуют свойствам измеряемого объекта. Если применить формулу алгебры 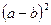 и свойства
и свойства 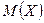 , то получим формулу для вычисления дисперсии:
, то получим формулу для вычисления дисперсии:
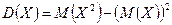 , так как
, так как 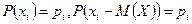 ,
,
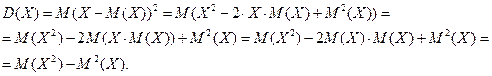
Итак, получили более удобное правило для вычисления дисперсии: дисперсия случайной величины  равна разности математического ожидания ква драта случайной величины
равна разности математического ожидания ква драта случайной величины  и квадрата математического ожидания случайной величины
и квадрата математического ожидания случайной величины 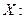
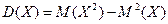 .
.
Замечание. Если 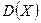
 сравнительно малое число, то значения д.с.в.
сравнительно малое число, то значения д.с.в.  близки к ее
близки к ее 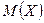 . Если
. Если 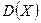 – большое число, то значения д.с.в.
– большое число, то значения д.с.в.  сильно рассредоточены относительно
сильно рассредоточены относительно 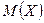 .
.
Cвойства дисперсии дискретной случайной величины.1. Дисперсия постоянной величины 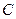 равна нулю:
равна нулю:
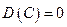 .
.
Пусть случайная величина  принимает только одно возможное значение
принимает только одно возможное значение 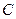 с вероятностью
с вероятностью 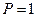 . Тогда, эта величина сохраняет свое значение
. Тогда, эта величина сохраняет свое значение 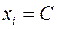 , рассеяния не имеет и является константой при всех реализациях:
, рассеяния не имеет и является константой при всех реализациях:
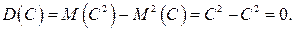
2. Постоянный множитель выносится за знак дисперсии в квадрате,т.е.
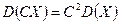 ,
,
где 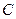 и
и  – независимые случайные величины. В самом деле,
– независимые случайные величины. В самом деле,
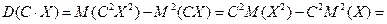
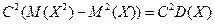 .
.
3. Дисперсия алгебраической суммы случайных величин равна сумме дисперсий этих случайных величин:
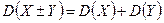 ,
,
где  и
и 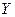 – независимые случайные величины.
– независимые случайные величины.
4. При изменении случайной величины  на постоянную
на постоянную 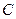 значение дисперсии не изменяется:
значение дисперсии не изменяется:
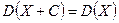 .
.
Поскольку случайные величины  и
и 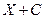
 отличаются только началом отсчета, такие величины рассеяны вокруг
отличаются только началом отсчета, такие величины рассеяны вокруг 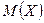
 и, соответственно,
и, соответственно, 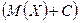 одинаково.
одинаково.
Дисперсия имеет размерность квадрата случайной величины:
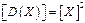 ,
,
где квадратными скобками обозначена размерность заключенной в них величины. С целью приведения меры рассеивания случайной величины к ее собственной размерности введено понятие среднего квадратического отклонения.
Определение 13.16.Арифметическое значение квадратного корня из дисперсии случайной величины  называется средним квадратическим отклонением и обозначается через
называется средним квадратическим отклонением и обозначается через
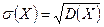 .
.
Следовательно,
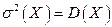 .
.
Заметим, что когда из контекста ясно о какой величине идет речь, символ д.с.в. опускают и записывают 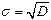 или
или 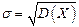 , и дисперсию обозначают через
, и дисперсию обозначают через 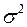 .
.
Пример 13.8.Пусть случайная величина  задана следующим законом:
задана следующим законом:
| Х | |||||||
| Р | 0,05 | 0,15 | 0,3 | 0,35 | 0,1 | 0,05 | 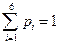 |
Найти 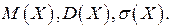
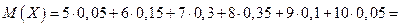
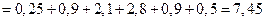 .
.
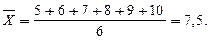
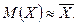
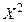 | ||||||
| Р | 0,05 | 0,15 | 0,3 | 0,35 | 0,1 | 0,05 |
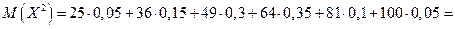
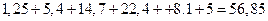 .
.
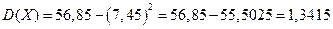 .
.
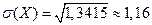 .
.
Биномиальное распределение вероятностей.Современная теория вероятностей, где это только возможно, переходит от схемы случайных событий к схеме случайных величин, которая по сравнению с первой представляет гораздо более гибкий и универсальный аппарат для решения задач, относящихся к случайным явлениям.
Определение 13.17. Если вероятности каждого из возможных значений случайной величины вычисляются по формуле Бернулли
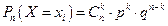 ,
,
то говорят, что случайная величина подчиняется биномиальному закону распределения или биномиальному распределению, а сама дискретная величина называется биномиальной.
Такое название распределение получило потому, что правая часть формулы Бернулли представляет собой общий член разложения бинома:
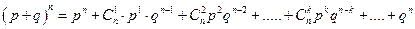 .
.
Ряд распределения биноминальной случайной величины имеет вид:
 | …. | k | ….. | n | |||
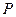 | 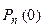 | 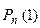 | 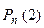 | …. | 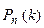 | … | 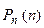 |
Зная значения величин n и р, можно составить ряд распределения и изобразить полигон распределения для конкретной биномиальной величины, т.е. p и n являются параметрами биномиального распределения.
Вероятность попадания биномиальной величины в заданный интервал. Если случайная величина дискретна, то вероятность попадания такой величины в заданный интервал равна сумме вероятностей отдельных значений этой величины, охватываемых заданным интервалом, т.е.
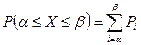 ,
,
где 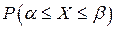 – искомая вероятность;
– искомая вероятность; 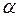 -левая граница интервала;
-левая граница интервала; 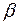 -правая;
-правая; 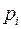 – вероятности отдельных значений, m – число значений дискретной случайной величины, принадлежащих отрезку
– вероятности отдельных значений, m – число значений дискретной случайной величины, принадлежащих отрезку 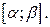
Так как биномиальная величина 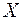 принимает значения из множества
принимает значения из множества 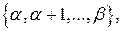 то
то
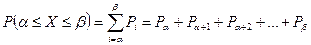 ,
,
где 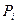 рассчитываются по формуле Бернулли.
рассчитываются по формуле Бернулли.
Иногда в задачах на повторные испытания не указываются левая или правая границы интервала. В этих случаях принимают соответственно 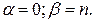
Определить вероятность случайной величины  – числа появления события
– числа появления события 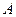 :
:
· не менее 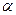 раз, т.е. Х
раз, т.е. Х 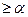 , тогда
, тогда 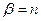 и случайная величина
и случайная величина  определяется неравенством
определяется неравенством 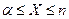 ,а
,а
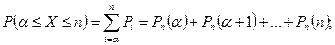
· более 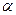 т.е.
т.е. 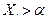 ;
; 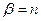 и
и 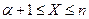 , а
, а
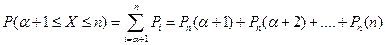
· не более 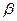 раз, т.е.
раз, т.е. 
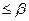 тогда
тогда 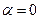 и
и 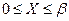 , а
, а
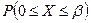 =
= 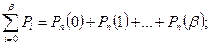
· менее 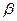 раз, т.е.
раз, т.е. 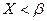 ;
; 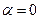 и
и 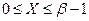 , а
, а
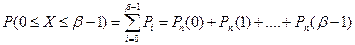 .
.
Замечание. Когда число слагаемых правой части данных формул более 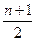 , то рациональнее перейти к событию, противоположному заданному, а затем вос-пользоваться свойством вероятностей противоположных событий.
, то рациональнее перейти к событию, противоположному заданному, а затем вос-пользоваться свойством вероятностей противоположных событий.
