Определение аналогов скоростей исследуемого механизма графическим методом

Решение этой задачи графическим методом основано на построении плана скоростей для первого положения механизма при j₁ = 136°18’.

Определим скорость точки A «пальца» кривошипа. Угловую скорость вращения кривошипа считаем равной угловой скорости выходного звена зубчатого механизма.

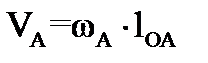, (4.2)

.

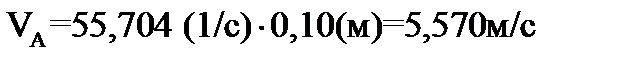Вектор 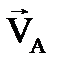перпендикулярен OA, и направлен в сторону вращения кривошипа, т.е. против часовой стрелки.

Определим скорости точки B, для чего составим векторное равенство:

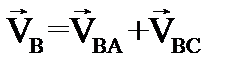(4.3)

Так как кулиса вращается вокруг оси, проходящей через точку O₁, то вектор 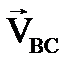направлен по касательной к окружности радиусом СB и, следовательно, перпендикулярен СB;

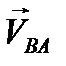- вектор скорости точки B относительно точки A; следовательно, вектор 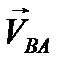перпендикулярен АB.

Таким образом, в равенстве (4.1)

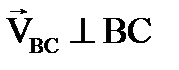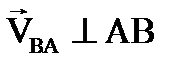; ; (4.4)

План скоростей строится в масштабе. Введем обозначения: P – полюс плана скоростей; 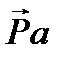– вектор, изображающий на плане скоростей скорость точки A ( 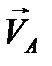) в масштабе 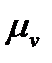. Масштабный коэффициент плана скоростей определяется по формуле:

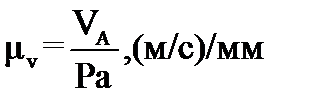, (4.5)

где 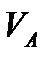– скорость точки A, м/с

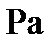– длина вектора 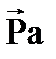, мм.

Для вычисления масштабного коэффициента 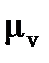примем длину отрезка 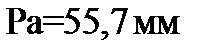, тогда по (12) вычислим

,

.

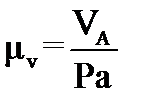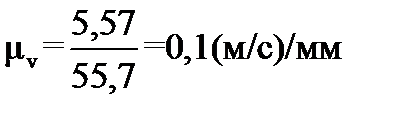Измерением на плане скоростей получим .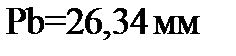

Скорость точки D определим, используя пропорции для плана скоростей:

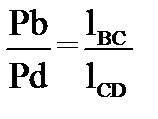
откуда следует:

,

.

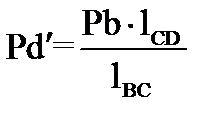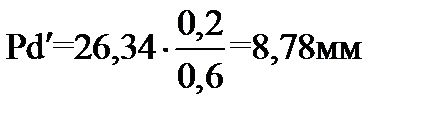где 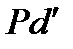и 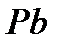– отрезки на плане механизма.

На плане скоростей точка 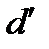лежит на продолжении прямой Pb.

Определим скорость точки d ползуна. Ползун D совершает горизонтальное движение, перпендикулярно DE и одновременно вертикальное движение по прямой DE.

На основании этого закончим построение плана скоростей: через точку 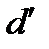проведем прямую, перпендикулярную звену DE, а через полюс P – вертикальную прямую; на их пересечении получим точку d. Измерением на плане скоростей получим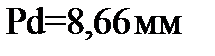

Используя масштабный коэффициент, 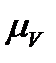вычислим скорости точек звеньев

,

,

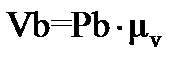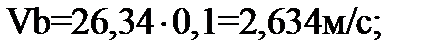
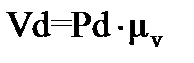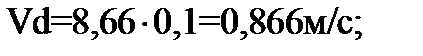
И скорости центров масс:

Угловые скорости звеньев:

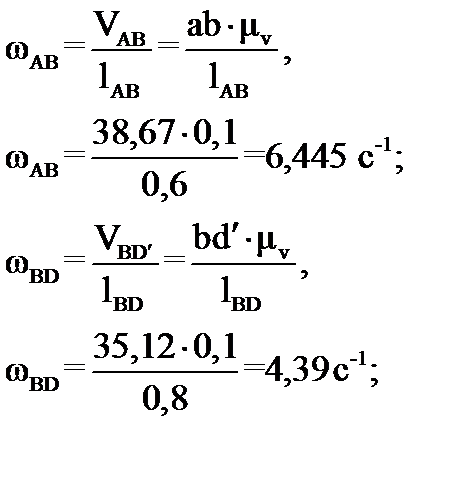
В результате построения получаем скорости точек и угловые скорости звеньев для каждого положения. Результаты построения сводим в таблице 4.2

Таблица 4.2 – Результат расчета линейных и угловых скоростей звеньев и центров масс.

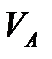		, м/с	, м/с	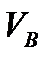, м/с	, м/с	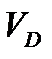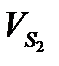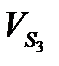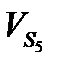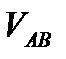, м/с	, м/с	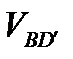, м/с	, м/с	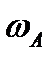, с-1	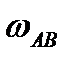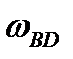, с-1	, с-1
	282˚47΄	5,570			2,78			5,6		55,704	9,34
	312˚47΄	5,570	2,64	0,86	3,9	1,46	0,26	3,86	3,52	55,704	6,44	4,4
	342˚47΄	5,570	4,9	1,62	5,22	2,72	0,48	1,26	6,54	55,704	2,1	8,18
	12˚47΄	5,570	5,9	1,96	5,7	2,96	0,58	1,36	7,86	55,704	2,26	9,82
	42˚47΄	5,570	5,18	1,72	5,08	2,6	0,52	3,54	6,92	55,704	5,9	8,66
	72˚47΄	5,570	2,9	0,96	3,66	1,46	0,28	5,04	3,86	55,704	8,4	4,82
крх	98˚48΄	5,570			2,78			5,6		55,704	9,34
	132˚47΄	5,570	3,46	1,14	4,04	1,74	0,34	4,58	4,62	55,704	7,64	5,78
	162˚47΄	5,570	5,28	1,76	5,34	2,64	0,52		7,04	55,704	3,34	8,8
	192˚47΄	5,570	5,46	1,82	5,48	2,74	0,54	1,34	7,28	55,704	2,24	9,1
	222˚47΄	5,570	4,38	1,44	4,54	2,2	0,44	4,22	5,84	55,704	7,04	7,3
	252˚47΄	5,570	2,5	0,82	3,12	1,26	0,24	5,76	3,34	55,704	9,6	4,18

Построение плана ускорений.

Определим ускорение 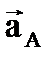точки 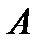«пальца» кривошипа. В общем случае

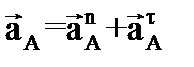, (4.6)

где 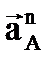– нормальное ускорение; 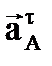– тангенциальное ускорение.

Определим численно .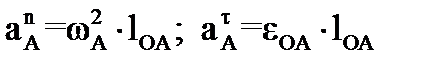

По условию задачи, кривошип вращается равномерно, т.е. 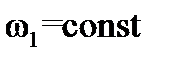. Следовательно, его угловое ускорение 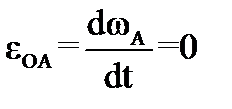и 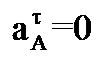, а полное ускорение точки A равно ее нормальному ускорению:

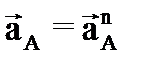
Таким образом, ускорение точки A:

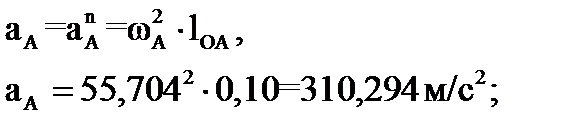
вектор 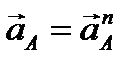направлен вдоль OA.

Из полюса плана ускорений π проводим вектор нормального ускорения точки А – вектор πa длиной 62,06 мм в направлении от точки A к точке O параллельно звену OA. Тогда масштабный коэффициент плана

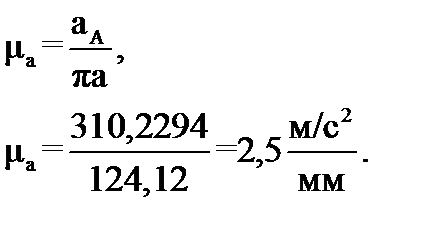
План ускорений для группы Ассура (2–3) строим графически, решая систему векторных уравнений:

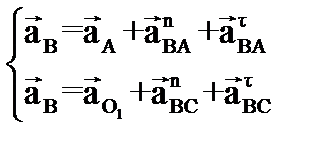
где .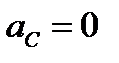

Величину нормального относительного ускорения определим как

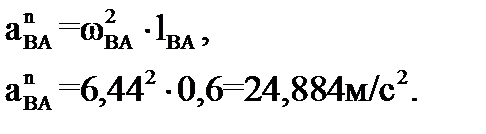
Направлен этот вектор от точки В к точке А параллельно шатуну АВ в направлении от точки В к точке А, а его длина в масштабе плана

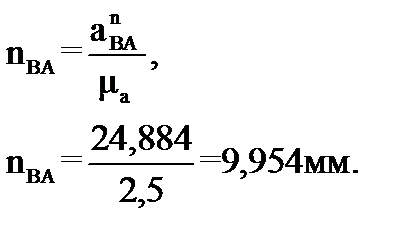
Величину нормального ускорения 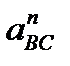рассчитаем как

.

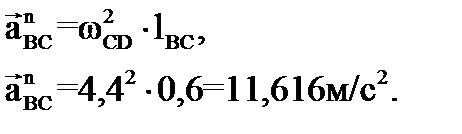Направлен этот вектор от точки В к точке O параллельно коромыслу в направлении от точки В к точке O, а его длина в масштабе плана

.

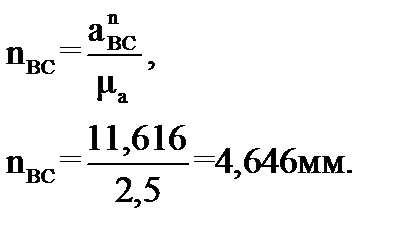Кроме этого, 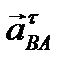^AВ и 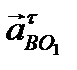^ ВO₁.

Из точки a плана ускорений проводим вектор 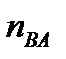нормального относительного ускорения, а через его конец – линию, перпендикулярную шатуну АВ (направление ускорения 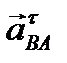). Из полюса π проводим вектор 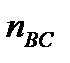, а через его конец – линию действия касательного ускорения 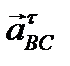перпендикулярно коромыслу ВС. Точка пересечения линий действия ускорени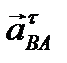й и 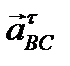даст точку b конца вектора полного ускорения точки B.

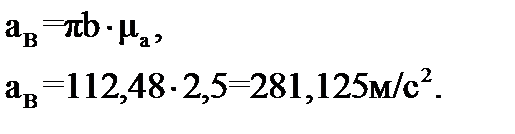
Чтобы построить план ускорений для группы Асура (4-5) необходимо найти скорость точки D из условия подобия .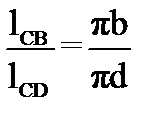

Из этого следует:

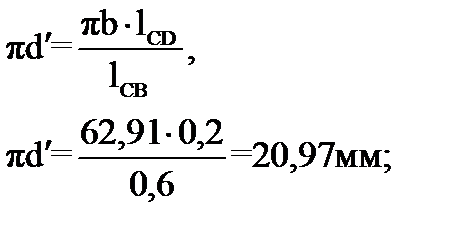
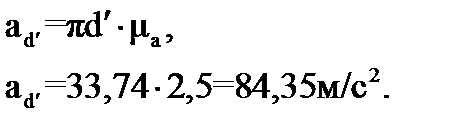
План ускорений для группы Ассура (4-5) строим, графически решая систему векторных уравнений

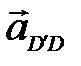– горизонталь

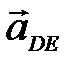– вертикаль.

Через точку d' плана проводим горизонталь, а через полюс проводим вертикальную линию. Точка пересечения этих линий дает точку d - конец вектора ускорения ползуна.

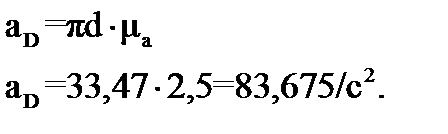
Для остальных положений механизма построение плана ускорений аналогично.

Рассчитываем полные ускорения точек центров масс звеньев (точки S₂, S₃, S₅), умножая длины соответствующих векторов πs_i на масштабный коэффициент плана ускорений

.
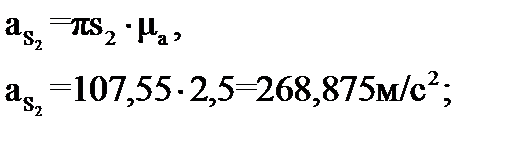
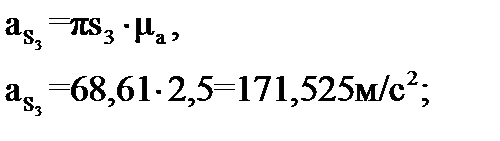
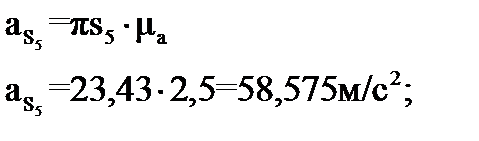