Общие понятия. Задача Коши. Теоремы существования и единственности

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

ПЕРВОГО ПОРЯДКА

Методические указания и индивидуальные задания

Самара 2010

Составитель: И.В. Алименков

УДК 517.912

Обыкновенные дифференциальные уравнения первого порядка: Метод.

Указания/ Самара.гос.аэрокосм.ун-т.

Сост. И.В. Алименков. Самара, 2010. 24 с.

В справочной форме приведены основные понятия теории обыкновенных дифференциальных уравнений первого порядка, формулировки теорем и методы решения. Рассмотрены также приближенные аналитические методы интегрирования уравнений первого порядка. Изложение сопровождается подробными решениями типовых примеров. Представлено 30 вариантов индивидуальных заданий, каждый из которых содержит 10 задач.

Работа выполнена на кафедре прикладной математики.

Библиография: 7 наименований.

Печатается по решению редакционно-издательского совета Самарского государственного аэрокосмического университета имени академика С.П.Королева.

Рецензент А.А.Дегтярев.

Содержание

Предисловие ………………………………………………………..…………………………. 4

1 Общие понятия. Задача Коши. Теоремы существования и единственности …………… 5

1.1 Уравнения, разрешенные относительно производной. Общее решение …………… 5

1.2 Задача Коши. Теорема существования и единственности …………………………... 5

1.3 Уравнения, не разрешенные относительно производной …………………………... 5

1.4 Особые решения ……………………………………………………………………….. 6

2 Уравнения, разрешенные относительно производной. Простейшие методы

интегрирования ……………………………………………………………………………... 6

2.1 Уравнения с разделенными и разделяющимися переменными …………………….. 6

2.2 Уравнение вида 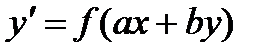………………………………………………………. 7

2.3 Однородные уравнения и приводящиеся к ним ……………………………………... 7

2.4 Обобщенно-однородные уравнения и приводящиеся к ним ……………………….. 8

2.5 Линейные уравнения …………………………………………………………………… 8

2.6 Уравнение Бернулли …………………………………………………………………… 9

2.7 Уравнение вида 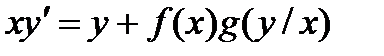……………………………………………….. 9

3 Уравнение в полных дифференциалах. Интегрирующий множитель …………………. 9

3.1 Уравнение в полных дифференциалах ………………………………………………. 9

3.2 Интегрирующий множитель ………………………………………………………….. 10

4 Уравнение Риккати ………………………………………………………………………… 10

4.1 Общее уравнение Риккати ………………………………………………………….... 11

4.2 Использование частных решений для построения общего решения ………………. 11

5 Уравнения, не разрешенные относительно производной ………………………………. 12

5.1 Метод «интегрирования посредством дифференцирования» …………………….. 12

5.2 Уравнения вида 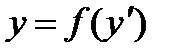……………………………………………………………..13

5.3 Уравнения вида 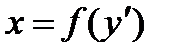……………………………………………………………..13

5.4 Уравнение Клеро ………..................................................................................... 13

5.5 Уравнение Лагранжа ………………………………………………………………….. 13

6 Приближенные аналитические методы решения уравнений …………………………… 14

6.1 Метод последовательных приближений (метод Пикара) ………………………….. 14

6.2 Метод разложения в ряд Тейлора по независимой переменной …………………… 14

6.3 Метод регулярного разложения по малому параметру ……………………………... 15

Варианты индивидуальных заданий ………………………………………………………... 16

Список литературы …………………………………………………………………………... 24

Предисловие

В данных методических указаниях рассматриваются дифференциальные уравнения

первого порядка, интегрируемые в квадратурах. Приведены краткие сведения из теории, разобраны типовые примеры и представлены 30 вариантов индивидуальных заданий.

Предназначены для студентов направлений 010501 - «Прикладные математика и информатика», а также 019600 - «Прикладные мате­матика и физика» в качестве руководства при подготовке к практическим занятиям и выполнению индивидуальных заданий.

Автор обращается к читателям с просьбой направлять свои отзывы о данной методической работе на кафедру прикладной математики Самарского государственного аэрокосмического университета имени академика С.П.Королева. Все критические замечания будут рассмотрены и учтены при следующих изданиях.

УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Общие понятия. Задача Коши. Теоремы существования и единственности

1.1 Уравнения, разрешенные относительно производной. Общее решение

Обыкновенное дифференциальное уравнение первого порядка, разрешенное относи­тельно производной, имеет вид

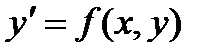. (1)

Иногда его записывают с помощью дифференциалов: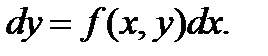

Решением дифференциального уравнения называется функция y(x), которая при

подстановке в уравнение обращает его в тождество. Общим решением дифференциального уравнения называется совокупность всех его частных решений. В ряде случаев общее решение удается записать в виде функции 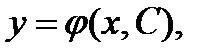зависящей от одной произвольной постоянной С ; при конкретных значениях С эта функция определяет конкретные решения уравнения (частные решения). На практике чаще встречается запись общего решения в неявном виде Ф(x,y,C) = 0 или в параметрической форме: x = x (t,C), y = y (t,C).

Геометрически общее решение (общий интеграл) представляет собой семейство

кривых на плоскости ху , зависящих от одного параметра С ; эти кривые называются интегральными кривыми данного уравнения. Частному решению (частному интегралу) соответствует одна кривая семейства, проходящая через заданную точку плоскости.

Уравнение 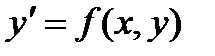для каждой точки (х,у) определяет значение 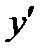, т.е. угловой

коэффициент касательной к интегральной кривой, проходящей через эту точку (задает поле направлений на плоскости ху ). Задача решения дифференциального уравнения первого порядка с геометрической точки зрения состоит в нахождении кривых, направление касательных к которым совпадает с направлением поля в соответствующих точках.

1.2 Задача Коши. Теорема единственности

§ Задача Коши : требуется найти решение уравнения (1), удовлетворяющее

начальному условию

у = у₀ при х = х₀ . (2)

Геометрический смысл задачи Коши: надо найти интегральную кривую уравнения

(1), проходящую через точку (х₀, у₀).

Условие (2) часто записывают в виде у(х₀) = у₀ .

§ Теорема единственности. Пусть функция f(х,у) непрерывна в замкнутой

области D и имеет там ограниченную частную производную по у (или выполняется условие Липшица: 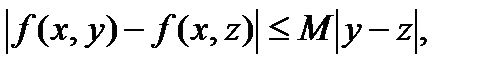где M – некоторая положительная константа). Тогда существует единственное решение уравнения (1), удовлетворяющее условию(2).

1.3 Уравнения, не разрешенные относительно производной.

В общем случае уравнения, не разрешенные относительно производной, имеют вид

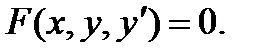(3)

§ Теорема существования и единственности. Существует единственное

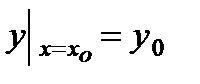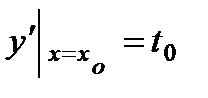решение у = у (х) уравнения (3), удовлетворяющее условиям и , где 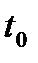- один из действительных корней уравнения 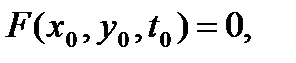если в некоторой окрестности точки 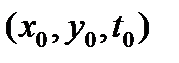выполнены условия:

1) Функция 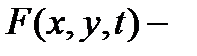непрерывна по всем трем аргументам;

2) Частная производная F_t существует и отлична от нуля;

3) Существует ограниченная по модулю частная производная F_y: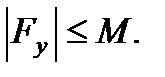

Указанное решение существует при 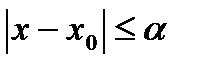, где 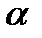> 0 – некоторое (достаточно малое) число.

1.4 Особые решения

§ Точки (х, у), в которых нарушается единственность решений уравнения (3),

называются особыми. Если удовлетворяются условия 1) и 3) теоремы существования и единственности, то в особых точках должны одновременно выполняться равенства

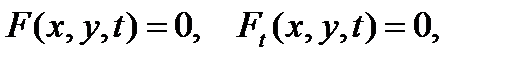(4)

которые представляют собой параметрическую запись t – дискриминантной кривой. Исключая из (4) параметр t, в ряде случаев можно получить уравнение этой кривой в неявном виде 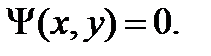Если какая-нибудь ветвь 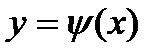кривой 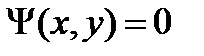состоит из особых точек и одновременно является интегральной кривой, то она называется особой интегральной кривой, а функция 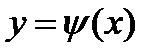– особым решением уравнения (3).

§ Особые решения можно найти путем определения огибающей семейства

интегральных кривых 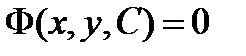уравнения (3). Огибающая входит в состав С -дискриминантной кривой, которая задается уравнениями .

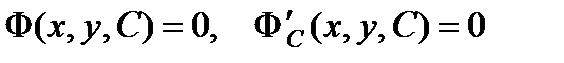Некоторая ветвь С - дискриминантной кривой будет огибающей, если на ней:

1) существуют ограниченные по модулю частные производные:

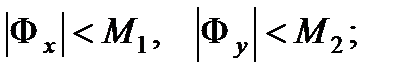
2)