Решение игры в смешанных стратегиях

Если игра не имеет седловой точки, то применение чистых стратегий не дает оптимального решения игры. В этих играх a < b. Применение минимаксных стратегий для каждого из игроков обеспечивает выигрыш, не превышающий a, и проигрыш, не меньший b. Естественным для каждого игрока является вопрос увеличения выигрыша (уменьшения проигрыша). Поиски такого решения состоят в том, что игроки применяют не одну, а несколько стратегий. Выбор стратегий осуществляется случайным образом. Случайный выбор игроком своих стратегий называется смешанной стратегией.

Смешанной стратегией S_A игрока А называется применение чистых стратегий A₂,…,A_i,…,A_m с вероятностями p₁, p₂,…,p_i,…,p_m, причем сумма вероятностей равна 1: 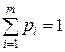р_i³0, i=1, 2, ... m. (*)

В игре, матрица которой имеет размерность m´n, стратегии игрока A задаются в виде матрицы S_A = 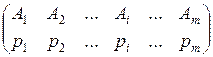или в виде строки вероятностей S_A=(p₁, p₂,…,p_i,…,p_m), с которыми игрок применяет свои первоначальные чистые стратегии. Эти наборы можно рассматривать как m-мерные вектора, для компонент которых выполняются условия (*).

Аналогично, для игрока B определяют n-мерные вектора S_B=(q₁, q₂,...,q_j,…,q_n) соответствующие его смешанным стратегиям.

При использовании смешанных стратегий выигрыш игрока A определяется как математическое ожидание выигрыша, т.е.

=

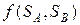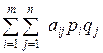
Чистые стратегии считаются частным случаем смешанных. На основании принципа минимакса определяется оптимальное решение ( или решение) игры: это пара оптимальных стратегий S*_A, S*_B в общем случае смешанных, обладающих свойством: если один из игроков придерживается своей оптимальной стратегии, то для другого не может быть выгодным отклоняться от своей. Выигрыш, соответствующий оптимальному решению, называется ценой игры n, которая удовлетворяет неравенству a £ n £ b .

Справедлива следующаяосновная теорема теории игр – теорема Неймана: каждая конечная игра имеет по крайней мере одно оптимальное решение, возможно, среди смешанных стратегий.

Пусть в игре m´n найдено решение, состоящее из двух оптимальных стратегий: S*_A= (р₁^*,р₂^*, …, р_m^*) и S*_B= (q₁^*, q₂^*, ... ,q_n^*). В общем случае, некоторые из чисел р_i^* и q_j^* , (i=1,2,…,m; j=1,2,….n) могут быть равными нулю, т.е. не все стратегии, доступные игроку входят в его оптимальную смешанную стратегию.

Чистые стратегии игроков А и В, входящие в оптимальные смешанные стратегии, для которых вероятности p_i и q_j отличны от нуля, называются активными.

Справедливатеорема об активных стратегиях. Если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры v, если второй игрок не выходит за пределы своих активных стратегий

Эта теорема имеет большое практическое значений – она дает конкретные модели нахождения оптимальных стратегий при отсутствии седловой точки.

Применение оптимальной стратегии позволяет получить выигрыш, равный цене игры a£n£b.

Применение игроком A оптимальной стратегии S*_Aдолжно обеспечивать ему при любых действиях игрока B выигрыш не меньше цены игры n. Поэтому выполняются следующие соотношения:

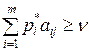, j=1,2,….n. (1)

Аналогично, для игрока B оптимальная стратегия S*_Bдолжна обеспечить при любых стратегиях игрока A проигрыш, не превышающий величину n, т.е. справедливо соотношение

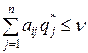, i=1,2,…,m. (2)

В дальнейшем соотношения (1) и (1) используются для решения игры.

Если игра m´n не имеет седловой точки, то отыскание ее решения, особенно при больших m и n, представляет собой довольно трудоемкую задачу. Иногда эту задачу удается упростить, если сократить число стратегий путем вычеркивания некоторых излишних (в частности, с помощью сокращения размерности матрицы), исключая излишние стратегии: дублирующие и заведомо невыгодные доминирующее.

Дублирующими называются стратегии, которым соответствуют одинаковые значения элементов в платежной матрице, т.е. она содержит одинаковые строки (столбцы).

Если все элементы i-ой строки матрицы меньше соответствующих элементов к-ой строки, то i-ая стратегия называется доминирующей. Аналогично, для столбцов.

Пример 3. Рассмотрим игру со следующей матрицей: .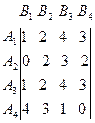

Из матрицы видно, что стратегия A₃ в точности повторяет (дублирует) стратегию A₁, поэтому любую из этих двух стратегий можно вычеркнуть. Далее, сравнивая почленно строки A₁ и A₂, видим, что все элементы строки A₂ меньше (или равны) соответствующих элементов строки A₁. Значит стратегия A₂ для нас, желающих выиграть, заведомо невыгодна. Вычеркивая A₃ и A₂, приведем матрицу к более простому виду: .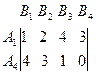

Таким образом, игра 4´4 сведена к игре 2´4.

Наиболее простой матричной конечной игрой является игра размером 2х2. Если игра имеет седловую точку, то оптимальное решение – это пара чистых стратегий, соответствующих этой точке.

Для игры, в которой нет седловую точки, в соответствии с основной теоремой теории игр оптимальное решение существует и определяется парой смешанных стратегий S*_A= (р₁^*,р₂^*) и S*_B= (q₁^*, q₂^*).

Для того чтобы найти их, воспользуемся теоремой об активных стратегиях. Если игрок А придерживается своей оптимальной стратегии S*_A, то его средний выигрыш останется неизменным и будет равен цене игры v, какой бы активной стратегией ни пользовался игрок B. Для игры 2х2 любая чистая стратегия противника является активной, если отсутствует седловая точка. Выигрыш игрока А (проигрыш игрока В) – случайная величина, математическое ожидание (среднее значение) которой является ценой игры. Поэтому средний выигрыш игрока А (оптимальная стратегия) будет равен v и для 1-й, и для 2-й стратегии противника. Пусть игра задана платежной матрицей: .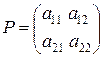

Средний выигрыш игрока А, если он использует оптимальную смешанную стратегию S*_A= 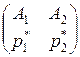, а игрок В – чистую стратегию В₁(это соответствует 1-му столбцу платежной матрицы Р), равен цене игры v: .

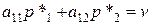Тот же средний выигрыш получает игрок А, если 2-й игрок применяет чистую стратегию В₂, т.е. 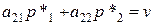. Учитывая, что р*₁ + р*₂ = 1, получаем систему уравнений для определения оптимальной стратегии S*_A и цены игры v:

(*).

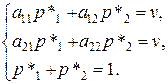Решая эту систему, получим оптимальную стратегию:

р*₁ = 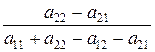, р*₂ = 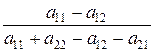. (3)

Подставляя значения р*₁ и р*₂ в одно из уравнений (*), получим:
v = 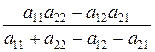. (4)

Применяя теорему об активных стратегиях при отыскании S*_B - оптимальной стратегии игрока B, получаем, что при любой чистой стратегии игрока А (А₁ или А₂) средний проигрыш игрока В равен цене игры v, т.е.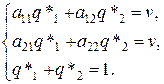

Тогда оптимальная стратегия S*_B (q*₁,q*₂):

q*₁= 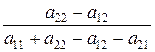, q*₂ = 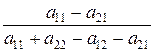. (5)

Пример 4. Найти решение игры, заданной матрицей 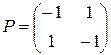из примера 1.

Решение. Имеем a=-1, b=1; матрица не имеет седловой точки.

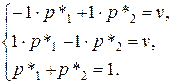
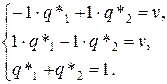
Находим оптимальные стратегии и цену игры: р*₁=р*₂= q*₁=q*₂=1/2, v =0.

Это означает, что оптимальная стратегия каждого игрока состоит в том, чтобы чередовать свои чистые стратегии случайным образом, выбирая каждое из убежищ с вероятностью 1/2, при этом средний выигрыш равен 0.