ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ №2
Основные понятия и определения линейного программирования
Линейное программирование – это раздел математики, в котором изучаются методы нахождения наименьшего или наибольшего значения линейной функции, на неизвестные которой наложены линейные ограничения. Решение начинается с составления экономико-математической модели.
Экономико-математическая модель - это выражение экономической задачи в виде функций, уравнений, неравенств.
Математическая модель задачи линейного программирования (ЗЛП) содержит:
1) совокупность переменных, которые должны быть неотрицательны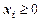 
.
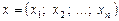2) целевую функцию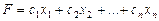 
.
3) условия (систему ограничений), налагаемые на переменные записанные в виде уравнений или неравенств.
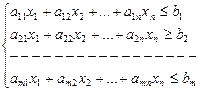(1)
Оптимальным решением (или оптимальным планом) называется такое решение системы ограничений, при котором целевая функция принимает оптимальное (max или min) значение.
Систему ограничений (1) заданную в виде неравенств можно привести к системе уравнений, для чего нужно к левой части неравенства прибавить или отнять добавочную переменную. Таким образом, ЗЛП приводится к канонической форме, когда система ограничений задана в виде системы m линейных уравнений с n переменными.
При этом возможны три случая:
1. Система ограничений несовместна. Следовательно, ЗЛП не имеет решения.
2. Система ограничений совместная и определенная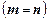 
. В этом случае система имеет единственное решение 
.
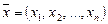3. Система ограничений совместная и неопределенная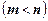 
. У такой системы существует бесчисленное множество решений.
Любые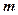 
переменных системы линейных уравнений с 
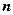переменными 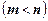называются основными (или базисными), если определитель из коэффициентов при них отличен от нуля. Этот определитель будем называть базисным минором матрицы А, из коэффициентов при переменных.
Тогда остальные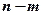 
переменных называются неосновными или свободными.
Основными могут быть различные группы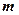 
переменных из 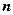, но их количество не превышает числа сочетаний из 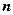по :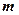
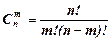
Из бесчисленного множества решений выделяют базисные решения.
Базисным решением системы 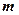линейных уравнений с 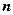переменными 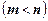называется решение, в котором неосновные переменные равны нулю.
Каждой группе основных переменных соответствует одно базисное решение. Базисные решения могут быть допустимыми или недопустимыми.
Базисное решение называется допустимым, если значения 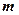основных переменных неотрицательны, а 
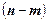неосновные переменные равны нулю.
Базисное решение называется недопустимым, если хотя бы одно значение переменной отрицательно.
Если в базисном решении хотя бы одна из основных переменных принимает нулевое значение, то оно называется вырожденным.