Ряд, многоугольник и функция распределения дискретной случайной величины.
Закон распределения случайной величины может быть представлен рядом распределения, многоугольником распределения, функцией распределения.
Дискретная случайная величина 
, имеющая конечное множество возможных значений 
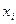с соответствующими им вероятностями 
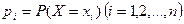может быть задана рядом распределения следующего вида табл. 1:
Таблица 1
| |  |  | … |  |
 |  |  | … |  |
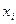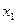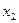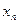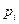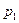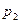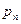Для вероятностей 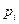, приведенных в таблице 1, должно выполняться условие:
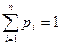(1).
Дискретная случайная величина, имеющая бесконечное множество значений 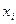с соответствующими им вероятностями 
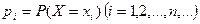может быть задана рядом распределения следующего вида (табл. 2):
Таблица 2
| | | | … | | … |
| | | | … | | … |
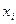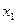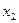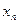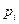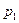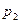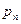Для вероятностей 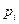, приведенных в таблице 2, должны выполняться условия: ряд
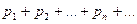сходится и 
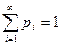(2).
Графически распределение случайной величины может быть представлено многоугольником распределения. Для построения многоугольника на плоскости в системе координат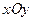 
строят точки 
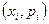и соединяют их ломанной линией. На рисунке 1 представлен многоугольник распределения случайной величины, число возможных значений которых равно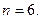 
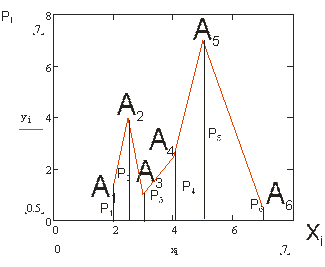
Рисунок 1.
Дискретная случайная величина может быть задана функцией распределения 
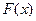, называемой также интегральной функцией распределения.
Для дискретной случайной величины, заданной рядом распределения (табл. 1 и2), значения функции распределения находят по формуле
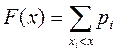, (3), где суммирование вероятностей 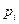ведут по всем тем значениям 
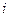, для которых 
.
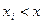Вероятность того, что случайная величина примет значения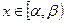 
выражается через функцию распределения формулой
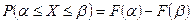. (4).
Задача образец
Игра состоит в набрасывании колец на колышки. Игрок получает четыре кольца и бросает по одному из этих колец до первого попадания на колышек. Вероятность попадания при каждом бросании равна 0,1. Найти ряд распределения случайной величины - числа неизрасходованных колец.
Решение. Игра, состоящая в набрасывании четырех колец на колышек, представляет собой осуществление независимых испытаний, в каждом из которых может появиться или не появиться событие 
- попадание кольца на колышек. Вероятность попадания при одном бросании равна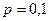 
, вероятность непопадания при одном бросании равна 
.
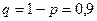Располагая четырьмя кольцами, игрок может набросить кольцо на колышек или при первом, или при втором, или при третьем, или при четвертом бросании, или же не набросить на колышек ни одного кольца. Возможные значения 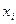случайной величины - числа неизрасходованных игроком колец будут следующими: 3, 2, 1, 0. пронумеруем 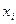в порядке их возрастания: 
.
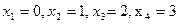Значение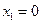 
величина примет тогда, когда произойдет одно из двух несовместных событий; первое из них – на колышек попало четвертое кольцо, второе событие – кольцо, брошенное четвертым, не попало на колышек. Вероятность события, состоящего в том, что примет значение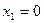 
, найдем , воспользовавшись теоремой умножения вероятностей независимых событий и теоремой сложения вероятностей несовместных событий:
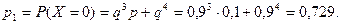
Значение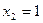 
величина примет тогда, когда игрок израсходует три кольца, т. е. совместно произойдут события: два брошенных кольца не попали, а третье кольцо попало на колышек.
Вероятность события, состоящего в том, что примет значение 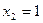найдем по теореме умножения вероятностей независимых событий:
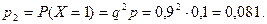
На основании рассуждения, аналогичного предыдущему, найдем
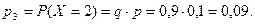
Вероятность события, состоящего в том, что примет значение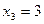 
равна 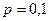, так как у игрока останется 3 кольца в том случае, если он попадет на колышек при бросании первого кольца. Итак,
.
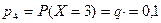Сложив, найденные вероятности, получим:
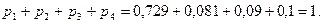
Свойство закона распределения о сумме вероятностей возможных значений случайной величины, отраженное формулой (1) выполнено.
Случайная величина имеет следующий ряд распределения:
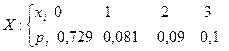
Задача № 1
Участник телевизионной игры за правильный ответ на каждый заданный ему вопрос получает пять баллов. Найти ряд распределения случайной величины - числа баллов, которое может получить участник телевизионной игры за правильный ответ на один вопрос, если имеется два варианта ответов на вопрос и этот участник будет отвечать наугад.
Задача № 2
Найти ряд распределения случайной величины - числа выпадений 6 очков при одном бросании игральной кости.
Ответ:
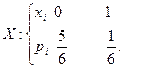
Задача № 3
Найти ряд распределения случайной величины - числа очков, выпадающих при одном бросании игральной кости.
Задача № 4
Фермер содержит 15 коров, 5 из которых дают удои более, чем по 4500 л молока в год. Случайным образом отобраны три принадлежащие фермеру коровы. Найти закон распределения случайной величины Найти ряд распределения случайной величины - числа коров, дающих указанные высокие удои среди отобранных.
Указание для нахождения вероятностей использовать формулу: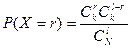 
Ответ: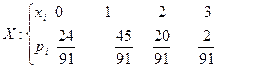 
.
Задача № 5
Изделия испытывают на прочность при работе в перегрузочных режимах. Вероятность для каждого изделия пройти испытание равна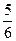 
и не зависит от исходов испытаний других изделий. Испытания заканчиваются сразу же после того, как появиться первое изделие не выдержавшее проверку на прочность. Найти ряд распределения случайной величины - числа производимых испытаний. Указание сумма бесконечно убывающей геометрической прогрессии: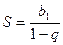 
.
Ответ: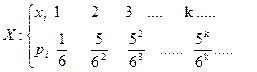 
.
Тема 6. Числовые характеристики дискретных случайных величин.
Математическое ожидание дискретной случайной величины , имеющей конечное число возможных значений, равно
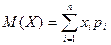, (1).
Математическое ожидание дискретной случайной величины , имеющей бесконечное число возможных значений, равно
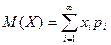, (2).
Причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
В формулах (1) и (2): 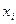- возможные значения случайной величины , 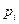- вероятности того, что случайная величина примет эти значения.
Свойства математического ожидания:
1. 
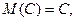(3).
Где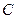 
- постоянная величина.
2. 
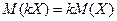, (4).
Где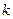 
=const.
3. 
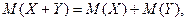(5).
Где и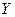 
- две любые случайные величины.
4. 
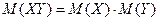, (6).
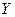Где и - две независимые случайные величины.
Дисперсия случайной величины определяется равенством
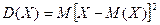, (7)
Или равносильным ему равенством
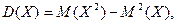(8).
Дисперсию дискретной случайной величины, имеющей конечное число возможных значений, можно вычислять по формуле
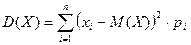, (9).
Соответствующей формуле (7), или по формуле
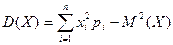, (10),
соответствующей формуле (8).
Свойства дисперсии:
1. 
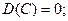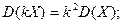(11)
2. 
(12)
3. 
; (13), где и 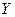- две независимые случайные величины.
Среднее квадратическое отклонение случайной величины равно
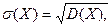(14).
Задача образец
Дискретная случайная величина задана рядом распределения
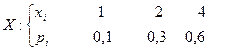
Найти ее математическое ожидание, дисперсию и среднее квадратическое отклонение.
Ответ: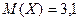 
; 
; 
 |
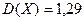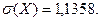
| определяем количество переменных, для того чтобы сделать 1..3 надо нажать ":" |
| для того, чтобы получить xi надо нажать "[", и для того, чтобы вставить данные в столбец надо нажимать ",". |
 |
 |
 |
 |
 |
 |
 |
 |
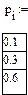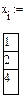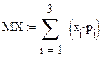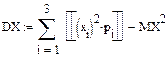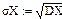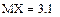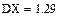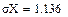Задача № 2
В результате обработки данных многолетних наблюдений получены распределения случайных величин и 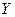числа хозяйств в каждом из двух районов области, которых урожайность зерновых культур может превысить 35 ц/га.
Для первого района области:
.
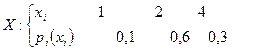Для второго района области:
.
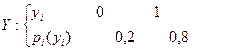Найти математическое ожидание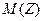 
и дисперсию 
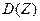случайной величины 
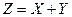двумя способами:
А) исходя из закона распределения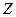 
;
Б) используя свойства математического ожидания и дисперсию, отраженные формулами (5) и (13).
Убедиться в том, что в условиях данной задачи эти свойства независимых случайных величин выполняются.
Ответ: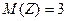 
; 
.
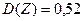Указание: надо найти все возможные значения случайной величины 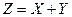и вероятности 
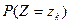этих значений. Для этого надо учесть следующее, что суммой (разностью или произведением) случайных величин 
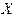и 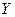называется случайная величина , которая принимает все возможные значения вида 
( 
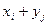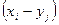или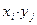 
), где 
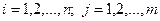с вероятностями 
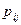того, что случайная величина примет значение 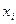, а 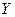- значение 
:
.
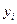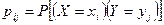Если случайные величины и 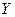независимы, то по теореме умножения вероятностей независимых событий
.
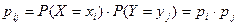Для конкретного примера:
1. 
;
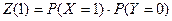2. 
;
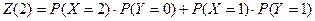3. 
;
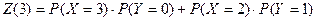4. 
.
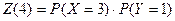Для расчета вероятностей удобно составить следующую таблицу:
Получим следующий ряд распределения
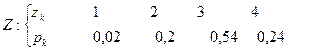
Далее необходимо рассчитать 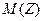и 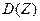, а также 
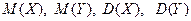и убедиться , что справедливы свойства математического ожидания и дисперсии.
Задача № 3.
Найти математическое ожидание случайной величины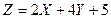 
, если известны математические ожидания 
, 
.
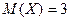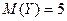Ответ: 31.
Задача № 4.
Доказать, что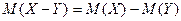 
.
Задача № 5.
Доказать, что для независимых случайных величин 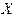и 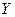справедливо равенство: 
.
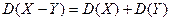Задача № 6.
Случайные величины и 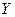. Известны дисперсии этих величин: 
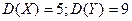. Найти дисперсию случайной величины 
.
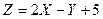Ответ: 29.
Задача № 7.
На птицефабрике три терморегулятора работают независимо друг от друга. Вероятность бесперебойной работы в течении смены первого терморегулятора равна 0,6. для второго и третьего эти вероятности соответственно равны 0,8 и 0,9. найти закон распределения случайной величины - числа терморегуляторов, бесперебойно работающих в течение смены. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение величины .
Ответ:
.
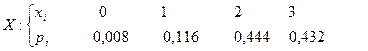
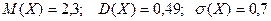Указание. Рассмотреть события:
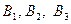- в течение смены будут бесперебойно работать соответственно первый, второй, третий терморегуляторы.
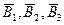- в течение смены не будут бесперебойно работать соответственно первый, второй, третий терморегуляторы.
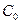- будут сбои в работе трех терморегуляторов;
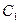- бесперебойно будет работать один терморегулятор;
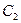- бесперебойно будут работать два терморегулятора;
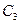- бесперебойно будут работать три терморегулятора.