Область существования функции
Задача2.19
Найти область существования функции 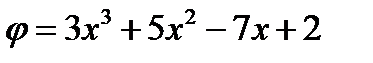 .
.
Решение.
Заданная функция – целая рациональная функция. Ее областью существования являются бесконечный интервал 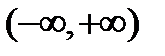 , или в другой записи
, или в другой записи  .
.
Задача2.20
Найти область существования функций:
1) 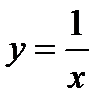 ;
;
2) 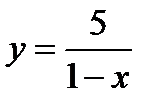 ;
;
3) 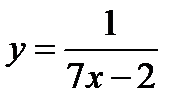 .
.
Решение.
1) Функция 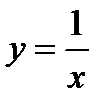 —дробная рациональная функция. Она существует при всех значениях независимой переменной
—дробная рациональная функция. Она существует при всех значениях независимой переменной 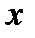 , кроме тех, которые обращают в нуль ее знаменатель, т.е. в данном случае кроме
, кроме тех, которые обращают в нуль ее знаменатель, т.е. в данном случае кроме 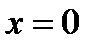 . Область существования этой функции состоит из двух бесконечных интервалов
. Область существования этой функции состоит из двух бесконечных интервалов 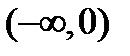 и
и 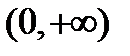 , или в другой записи
, или в другой записи 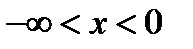 и
и 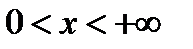 .
.
2) Функция 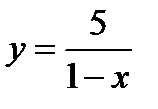 также определена при всех значениях
также определена при всех значениях 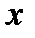 , кроме того его значения, при котором
, кроме того его значения, при котором 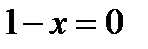 , т.е. кроме
, т.е. кроме 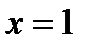 . Область существования состоит из двух бесконечных интервалов
. Область существования состоит из двух бесконечных интервалов 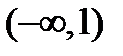 ;
; 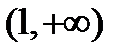 , или в другой записи
, или в другой записи 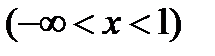 ;
; 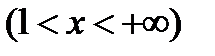 .
.
3) Решив уравнение 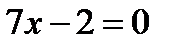 , найдем, что
, найдем, что 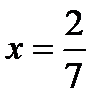 . Область существования функции
. Область существования функции 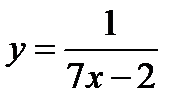 состоит из двух бесконечных интервалов
состоит из двух бесконечных интервалов 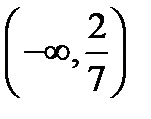 ;
; 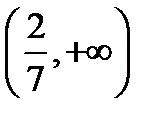 , или в другой записи
, или в другой записи 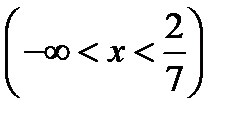 и
и 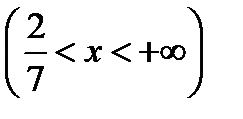 .
.
Задача2.21
(для самостоятельного решения). Определить область существования функций:
1) 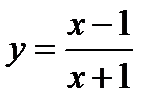 ;
;
2) 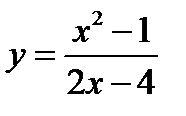 .
.
Ответ.
1) 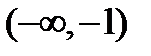 ;
; 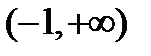 , или
, или 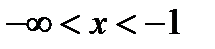 и
и 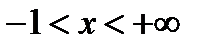 .
.
2) 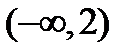 ;
; 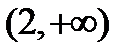 , или
, или 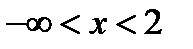 и
и 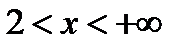 .
.
Задача2.22
Найти область существования функции 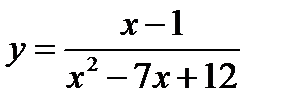 .
.
Решение.
Заданная функция – дробная рациональная функция. Она определена при всех действительных значениях 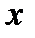 , кроме тех, при которых знаменатель дроби
, кроме тех, при которых знаменатель дроби 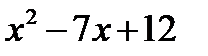 равен нулю, т.е. кроме значений
равен нулю, т.е. кроме значений 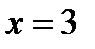 и
и 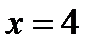 (эти значения найдены из уравнения
(эти значения найдены из уравнения 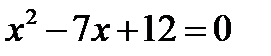 ). Область существования заданной функции состоит из трех интервалов:
). Область существования заданной функции состоит из трех интервалов: 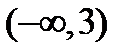 ;
; 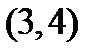 ;
; 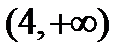 , или в другой записи:
, или в другой записи: 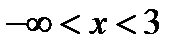 ;
;  ;
; 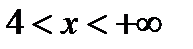 .
.
Задача2.23
(для самостоятельного решения). Определить область существования функций:
1) 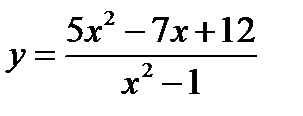 ;
;
2) 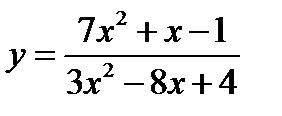 .
.
Ответ.
1) Область существования состоит из трех интервалов: 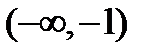 ;
; 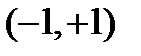 ;
; 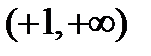 .
.
2) Область существования состоит из трех интервалов: 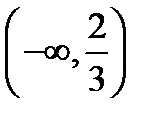 ;
; 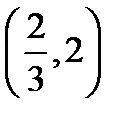 ;
; 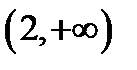 .
.
Задача2.24
Найти область существования функции 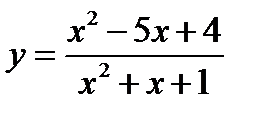 .
.
Решение.
Приравняв нулю знаменатель дроби 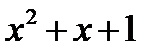 и решив квадратное уравнение
и решив квадратное уравнение 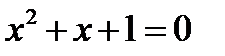 , убедимся что его корни – комплексные числа:
, убедимся что его корни – комплексные числа: 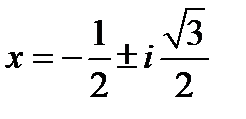 . Ни при одном действительном значении
. Ни при одном действительном значении 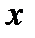 многочлен
многочлен 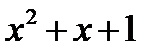 в ноль не обращается. Поэтому заданная функция определена при всех действительных значениях
в ноль не обращается. Поэтому заданная функция определена при всех действительных значениях 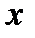 . Ее областью существования является бесконечный интервал
. Ее областью существования является бесконечный интервал 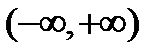 .
.
Задача2.25
(для самостоятельного решения). Найти область существования функций:
1) 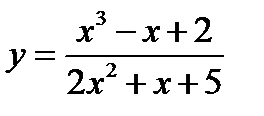 ;
;
2) 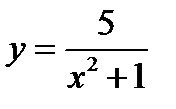 .
.
Ответ.
1) Бесконечный интервал 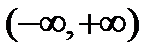 .
.
2) Бесконечный интервал 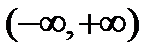 .
.
Задача2.26
(для самостоятельного решения). Найти область существования функций:
1) 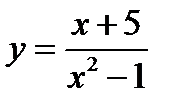 ;
;
Ответ.
1) Функция существует в двух бесконечных интервалах: 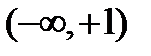 и
и 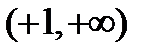 , т.е. При любом значении
, т.е. При любом значении 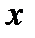 , кроме
, кроме 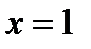 .
.
2) Знаменатель дроби 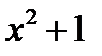 имеет один действительных корень
имеет один действительных корень 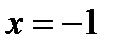 . Функция существует в двух бесконечных интервалах:
. Функция существует в двух бесконечных интервалах: 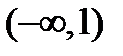 и
и 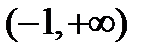 , т.е. при любом значении
, т.е. при любом значении 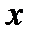 , кроме
, кроме 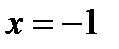 .
.
Задаче2.27
(для самостоятельного решения). Найти область существования функций:
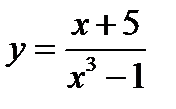
(знаменатель дроби 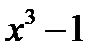 имеет действительный корень
имеет действительный корень 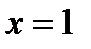 );
);
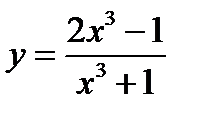 .
.
Решение.
1) Для того чтобы функция 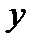 принимала только действительные значения, величина
принимала только действительные значения, величина 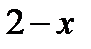 , стоящая под корнем, не должна принимать отрицательных значений, т.е. должно быть
, стоящая под корнем, не должна принимать отрицательных значений, т.е. должно быть 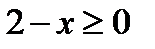 , откуда
, откуда 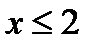 . Областью существования функции является совокупность действительных значений
. Областью существования функции является совокупность действительных значений 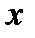 , меньших или равных 2, т.е. полуотрезок
, меньших или равных 2, т.е. полуотрезок 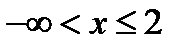 .
.
2) Чтобы определить область существования функции, составим неравенство 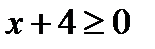 , из которого получаем, что
, из которого получаем, что 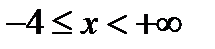
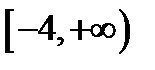 .
.
Задача2.28
(для самостоятельного решения). Найти область существования функций:
1) 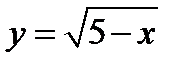 и 2)
и 2) 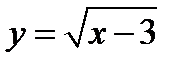 .
.
Ответ.
1) Полуотрезок 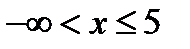 .
.
2) Полуотрезок 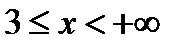 .
.
Задача2.29
Найти область существования функций
1) 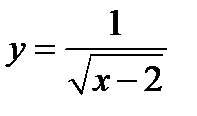 ;
;
2) 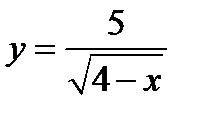 ;
;
3) 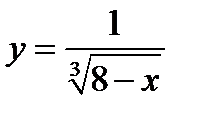 .
.
Решение.
1) Выражение  принимает действительное значение, когда
принимает действительное значение, когда 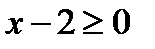 , т.е. когда
, т.е. когда 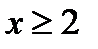 . Но при
. Но при 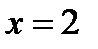 имеем
имеем 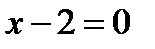 , знаменатель дроби обращается в ноль, дробь теряет числовой смысл, а поэтому значение
, знаменатель дроби обращается в ноль, дробь теряет числовой смысл, а поэтому значение  не может входить в область существования функции. Значит, функция существует при значениях
не может входить в область существования функции. Значит, функция существует при значениях 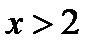 , область существования представляет собой бесконечный интервал
, область существования представляет собой бесконечный интервал 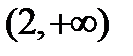 .
.
2) Областью существования функции является бесконечный интервал 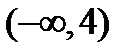 .
.
3) Область существования состоит из двух бесконечных интервалов 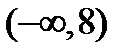 и
и 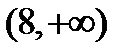 . Это же заключение можно записать с помощью неравенств:
. Это же заключение можно записать с помощью неравенств: 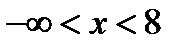 и
и 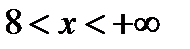 .
.
Задача2.30
(для самостоятельного решения). Определить область существования функций:
1) 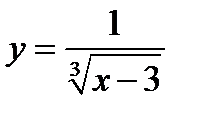 ;
;
2) 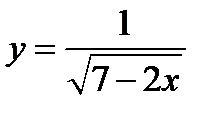 ;
;
3) 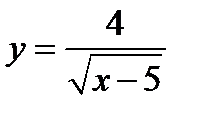 .
.
Ответ.
1) Два бесконечных интервала 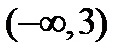 ;
; 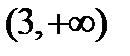 .
.
2) Бесконечный интервал 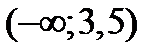 .
.
3) Бесконечный интервал 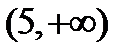 .
.
ТРЕТЬЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Продолжение упражнений в определении области существования функции.
Задача 3.1
Найти область существования функций:
1) 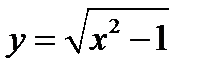 ;
;
2) 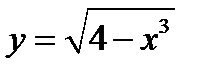
Решение.
1) Для того чтобы функция 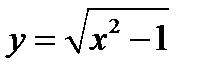 принимала только действительные значения, надо, чтобы
принимала только действительные значения, надо, чтобы 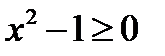 , т.е.
, т.е. 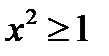 . Это неравенство выполняется тогда, когда
. Это неравенство выполняется тогда, когда 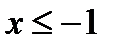 и
и 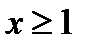 , и, таким образом, область существования функции состоит из двух полуотрезков:
, и, таким образом, область существования функции состоит из двух полуотрезков: 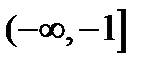 и
и 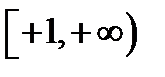 , или в другой записи
, или в другой записи 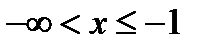 и
и 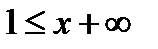 .
.
2) Должно выполнятся неравенство 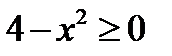 , т.е.
, т.е. 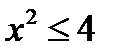 . Отсюда следует, что
. Отсюда следует, что 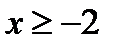 и
и 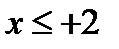 .
.
Областью существования функции является отрезок 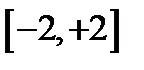 .
.
Это можно записать иначе: 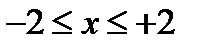 .
.
Задача 3.2
(для самостоятельного решения). Найти область существования функций:
1) 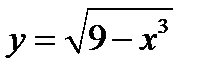 ;
;
2) 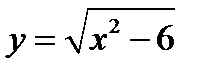 ;
;
3) 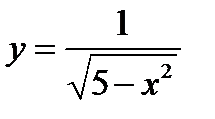 ;
;
4) 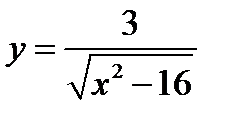 .
.
Ответ.
1) Отрезок 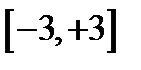 , иначе
, иначе 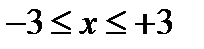 .
.
2) Два полуотрезка 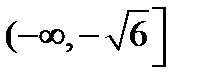 и
и 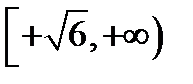 , иначе
, иначе 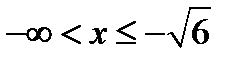 и
и  .
.
3) Интервал 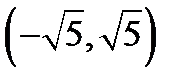 , или
, или 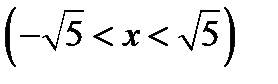 (значения
(значения 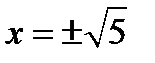 отбрасываются, так как при
отбрасываются, так как при 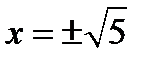 знаменатель дроби обращается в ноль и дробь теряет числовой смысл).
знаменатель дроби обращается в ноль и дробь теряет числовой смысл).
4) Два интервала 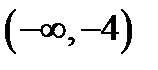 и
и 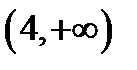 , или
, или 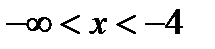 и
и 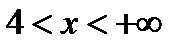 (значения
(значения 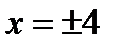 отбрасываются, так как при
отбрасываются, так как при 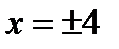 знаменатель дроби обращается в ноль и тем самым дробь теряет числовой смысл).
знаменатель дроби обращается в ноль и тем самым дробь теряет числовой смысл).
Задача 3.3
(для самостоятельного решения). Определить область существования функции 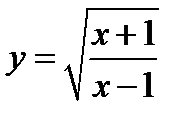 .
.
Указание. Должно выполнятся неравенство 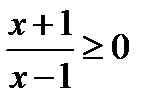 .Для определения тех значений
.Для определения тех значений 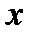 ,при которых это имеет место следует решить системы неравенств:
,при которых это имеет место следует решить системы неравенств:
1) 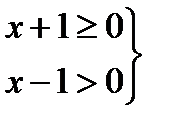
2) 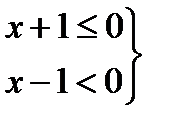
Из решения этих неравенств следует, сто областью существования является полуотрезок 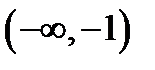 и интервал
и интервал 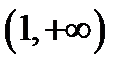 . Это можно записать иначе:
. Это можно записать иначе: 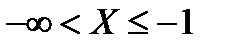 и
и 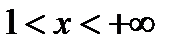 . Значение
. Значение 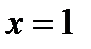 рассматриваться не может, так как тогда
рассматриваться не может, так как тогда 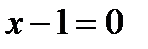 и дробь
и дробь 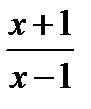 теряет числовой смысл.
теряет числовой смысл.
Задача 3.4
(для самостоятельного решения). Найти область существования функции 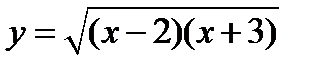 .
.
Указание. Рассмотрим неравенство 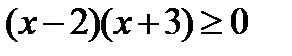 .
.
Ответ.
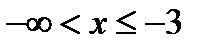 и
и  .
.
Задача 3.5
Найти область существования функции 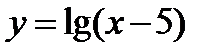 .
.
Решение.
Учитывая, что если основание логарифмов положительно, то ни ноль ни отрицательное числа логарифмов не имеют, область существования данной функции найдем из требования, чтобы 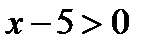 , откуда следует, что должно быть
, откуда следует, что должно быть 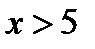 . Функция существует для значений
. Функция существует для значений 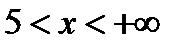 , т.е. на бесконечном интервале
, т.е. на бесконечном интервале 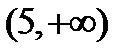 .
.
Задача 3.6
(ля самостоятельного решения). Найти область существования функций.
1) 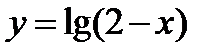 ;
;
2) 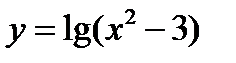 .
.
Ответ.
1) 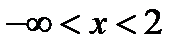 ;
;
2) 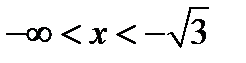 и
и 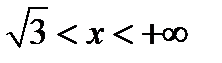 .
.
Указание. В случае 2) рассмотреть неравенство 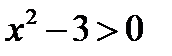 .
.
Задача 3.7
(для самостоятельного решения). Найти область существования функции 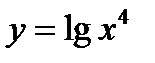 .
.
Ответ.
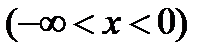 и
и 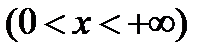 , т.е. Функция определена при любом значении
, т.е. Функция определена при любом значении 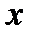 , кроме
, кроме 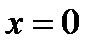 .
.
Задача 3.8
Найти область существования функции 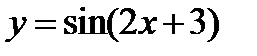 .
.
Решение.
Функция 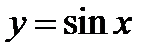 определена при любом значении аргумента
определена при любом значении аргумента 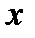 . Значит, выражение
. Значит, выражение 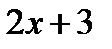 , стоящее под знаком синуса, может принимать любое значение, откуда следует, что
, стоящее под знаком синуса, может принимать любое значение, откуда следует, что 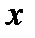 может принимать любое значение. Областью существования функции является бесконечный интервал
может принимать любое значение. Областью существования функции является бесконечный интервал 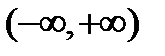 . Это заключение можно написать и иначе:
. Это заключение можно написать и иначе: 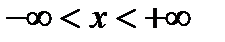 .
.
Задача 3.9
(для самостоятельного решения). Найти область существования функции 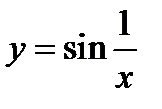 .
.
Ответ.
Все действительные числа кроме 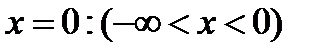 и
и 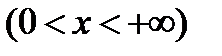 .
.
Задача 3.10
Найти область существования функции 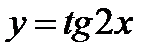 .
.
Решение.
Функция 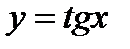 определена при всех действительных значениях
определена при всех действительных значениях 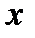 , кроме
, кроме 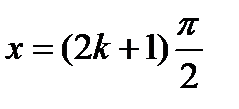 . Где
. Где 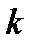 —любое целое число. Значит, в нашем случае величина
—любое целое число. Значит, в нашем случае величина 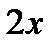 , стоящая после знака тангенса, не должна быть равна
, стоящая после знака тангенса, не должна быть равна 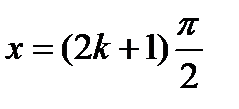 , т.е.
, т.е. 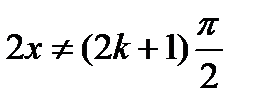 , а
, а 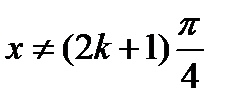 . Таким образом, область существования функции
. Таким образом, область существования функции 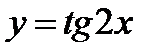 состоит из всех действительных чисел, кроме значений
состоит из всех действительных чисел, кроме значений 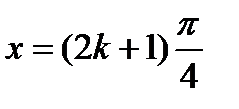 , где
, где 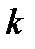 —любое целое число.
—любое целое число.
Задача 3.11
(для самостоятельного решения). Найти область существования функций: 1) 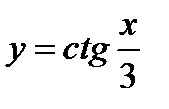 ; 2)
; 2) 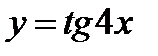 ; 3)
; 3) 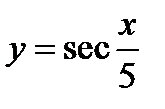 и
и 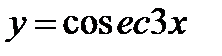 .
.
Ответ.
1) Множество всех действительных чисел, кроме значений 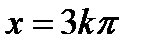 .
.
2) Множество всех действительных чисел, кроме значений 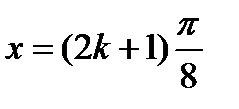 .
.
3) Множество всех действительных чисел, кроме 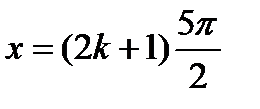 .
.
4) Множество всех действительных чисел, кроме 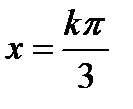 .
.
(всюду 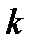 —любое целое число)
—любое целое число)
Задача 3.12
Найти область существования функции 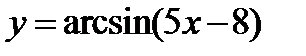 .
.
Решение.
Областью существования функции 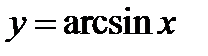 является отрезок
является отрезок 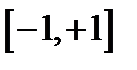 . Поэтому область существования данной функции указывается неравенствами
. Поэтому область существования данной функции указывается неравенствами 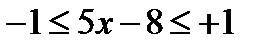 .
. 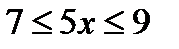 , откуда уже следует, что функция существует для значений
, откуда уже следует, что функция существует для значений 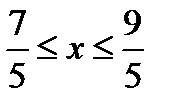 .
.
Задача 3.13
(для самостоятельного решения). Найти область существования функций:
1) 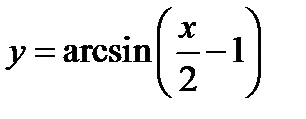 ;
;
2) 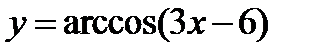 .
.
Ответ.
1) 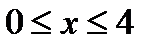 .
.
2) 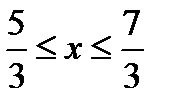 .
.
Задача 3.14
(для самостоятельного решения). Найти область существования функций:
1) 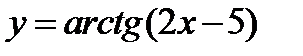 ;
;
2) 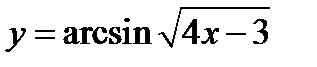 .
.
Ответ.
1) 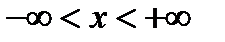 .
.
2) 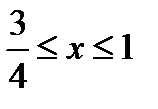 .
.
Задача 3.15
(для самостоятельного решения). Найти область существования функции 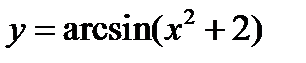 .
.
Ответ.
Данное аналитическое выражение не определяет никакой функции, так как ни при одном значении 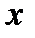 не имеют место неравенства
не имеют место неравенства  .
.
Указание. К решению задач 3.16—3.23.
Если требуется область существования алгебраической суммы некоторых функций, то надо поступить так:
1) Определить область существования каждой из слагаемых функций;
2) Определить часть, общую для всех найденных областей. Эта общая часть и будет искомой.
Если такой общей части у областей , найденных в п.1), не окажется, то заданное аналитическое выражение, представляющее алгебраическую сумму нескольких функций, не определяет никакой функции в области действительных чисел.
Это указание распространяется также на производные нескольких функций и на частное двух функций, причем при определении области существования частного двух функций должны быть исключены точки, в которых знаменатель дроби обращается в нуль.
Задача 3.16
Найти область существования функции 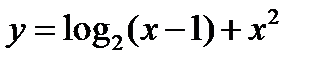 .
.
Решение.
Областью существования функции 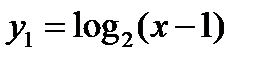 является совокупность всех значений
является совокупность всех значений 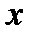 , удовлетворяющих неравенству
, удовлетворяющих неравенству 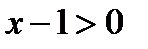 , т.е. интервал
, т.е. интервал 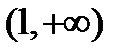 .
.
Областью существования степенной функции 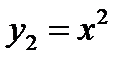 является интервал
является интервал 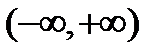 .
.
Общей частью этих двух интервалов является интервал 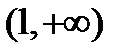 . Таким образом, данная функция существует для значений
. Таким образом, данная функция существует для значений 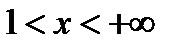 .
.
Задача 3.17
Найти область существования функции 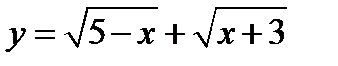 .
.
Решение.
Функция 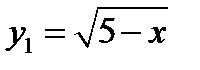 существует для значений
существует для значений 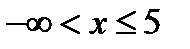 . Функция
. Функция 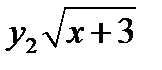 существует для значений
существует для значений 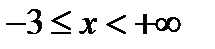 .
.
Общей частью найденных двух областей является отрезок 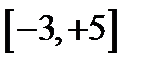 , а поэтому данная функция существует для значений
, а поэтому данная функция существует для значений 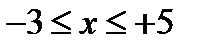 .
.
Задача 3.18
(для самостоятельного решения). Найти область существования функции 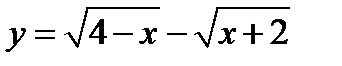 .
.
Ответ.
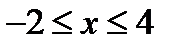 , т.е. отрезок
, т.е. отрезок 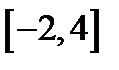 .
.
Задача 3.19
(для самостоятельного решения). Найти область существования функции 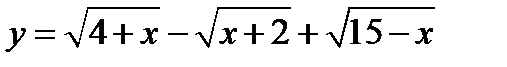
Ответ.
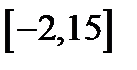 , т.е.
, т.е. 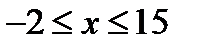 .
.
Задача 3.20
(для самостоятельного решения). Найти область существования функции 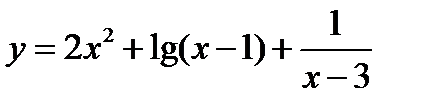 .
.
Ответ.
Функция существует для значений 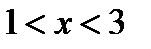 и
и 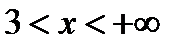 ,т.е. в интервалах
,т.е. в интервалах 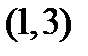 и
и 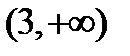 .
.
Задача 3.21
(для самостоятельного решения). Найти область существования функции  .
.
Ответ.
Функция существует при всех значениях 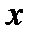 , кроме значений
, кроме значений 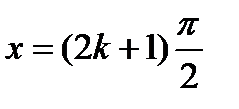 , где
, где 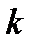 —любое целое число.
—любое целое число.
Задача 3.22
Найти область существования функции 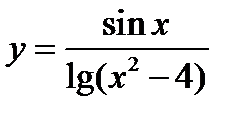 .
.
Решение.
Функция 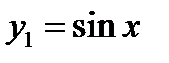 существует в бесконечном интервале
существует в бесконечном интервале 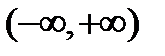 .
.
Функция 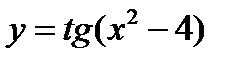 существует в интервалах
существует в интервалах 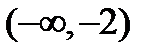 и
и 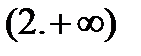 . Но следует иметь ввиду, что функция
. Но следует иметь ввиду, что функция 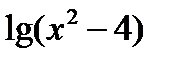 стоит в знаменателе дроби, а поэтому из этих двух интервалов надо исключить точки, в которых эта функция, обращается в нуль, т.е.точки, для которых
стоит в знаменателе дроби, а поэтому из этих двух интервалов надо исключить точки, в которых эта функция, обращается в нуль, т.е.точки, для которых 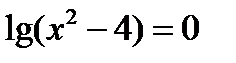 , или
, или 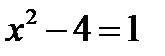 , а
, а 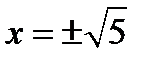 . Таким образом, функцию
. Таким образом, функцию 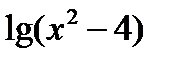 следует рассматривать в интервалах:
следует рассматривать в интервалах:
1) 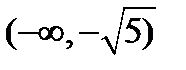 ;
;
2) 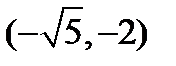 ;
;
3) 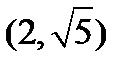 ;
;
4) 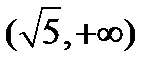 .
.
Общей частью, принадлежащей бесконечному интервалу 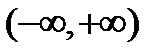 , в котором определена функция
, в котором определена функция 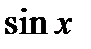 , и только что найденными интервалами являются именно эти интервалы, а поэтому данная функция существует в интервалах:
, и только что найденными интервалами являются именно эти интервалы, а поэтому данная функция существует в интервалах:
1) 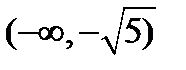 ;
;
2) 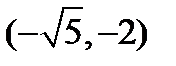 ;
;
3) 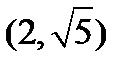 ;
;
4) 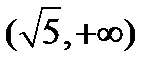 .
.
Задача 3.23
(для самостоятельного решения). Найти область существования функции 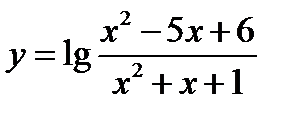 .
.
Ответ.
Два бесконечных интервала: 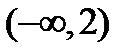 и
и 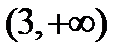 .
.
ЧЕТВЕРТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Построение графиков функции.
Это практическое занятие посвящается упражнениям на построение графиков функций, заданных аналитически.
В инженерной практике с построением графиков функций приходится встречаться очень часто. При изучении таких предметов, как сопротивление материалов, теория упругости, гидравлика, электротехника, радиотехника, к построению графиков функций приходится прибегать буквально на каждом шагу.
Поэтому студенту следует с исключительной серьезностью отнестись к этому практическому занятию.
К построению графиков более сложных функций мы еще возвращаемся на практическом занятии №35 и используем для этого уже аппарат дифференциального исчисления.
