Теорема про ділення з остачею
Математичний словник
Кільце многочленів над областю цілісності. НСД та НСК многочленів
Означення 1.Многочленом (поліномом) від однієї змінної над областю цілісності 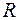 називається вираз виду
називається вираз виду
 (1)
(1)
де  - довільне ціле невід’ємне число,
- довільне ціле невід’ємне число, 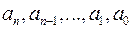 - елементи
- елементи 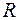 , а
, а 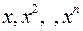 - деякі символи;
- деякі символи; 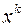 називається
називається 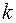 -м степенем змінної
-м степенем змінної  а
а 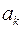 -
- 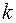 -м коефіцієнтом многочлена (1) або коефіцієнтом при
-м коефіцієнтом многочлена (1) або коефіцієнтом при 
Комутативне кільце, в якому не існує дільників нуля, називається областю цілісності.
Означення 2. Вираз 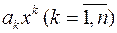 називається
називається 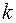 -м членом або членом
-м членом або членом 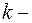 го степеня многочлена
го степеня многочлена
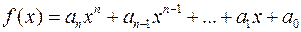 (2),
(2),
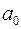 - нульовим або вільним членом многочлена (2).
- нульовим або вільним членом многочлена (2).
Означення 3. Відмінний від нуля член многочлена  степінь якого більший за степінь усіх інших відмінних від нуля членів цього многочлена, називається старшим членом, його коефіцієнти - старшими коефіцієнтами, а його степінь – степенем многочлена
степінь якого більший за степінь усіх інших відмінних від нуля членів цього многочлена, називається старшим членом, його коефіцієнти - старшими коефіцієнтами, а його степінь – степенем многочлена 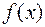 (позначається
(позначається 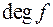 («degree» - «степінь»)).
(«degree» - «степінь»)).
Многочлени нульового степеня називаються також константами.
Дії над многочленами.
Нехай дано два многочлена
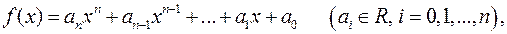
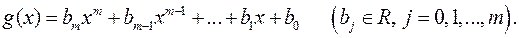
Означення 4. Многочлени 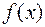 і
і 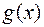 називаються рівними між собою і записують
називаються рівними між собою і записують  якщо канонічні форми цих многочленів збігаються, тобто
якщо канонічні форми цих многочленів збігаються, тобто
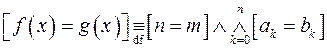 . (3)
. (3)
Якщо 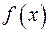 і
і 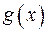 відмінні від
відмінні від 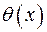 , то (3) можна переписати у вигляді
, то (3) можна переписати у вигляді
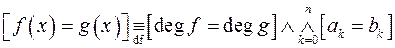 (4)
(4)
а для випадку нуль-многочлена можна записати
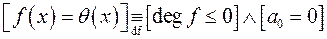 .
.
Нерівність 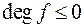 тут означає, що
тут означає, що 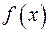 не має членів ненульового степеня.
не має членів ненульового степеня.
Означення 5. Сумою многочленів 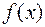 і
і 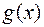 називається многочлен
називається многочлен
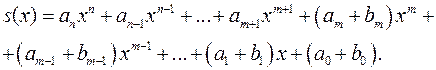
Те, що  є сумою многочленів
є сумою многочленів 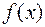 і
і 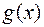 , записують так:
, записують так:
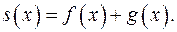
Означення 6.Добутком многочленів 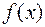 і
і 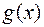 називається многочлен
називається многочлен
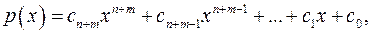
де
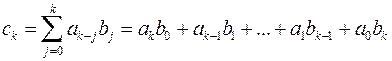
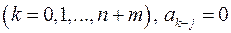 при
при 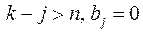 , при
, при 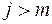 .
.
Те, що 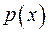 є добуток многочленів
є добуток многочленів 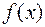 і
і 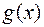 , записують так:
, записують так:
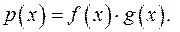
Наслідок 1. Якщо 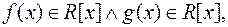 то і
то і
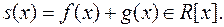
Наслідок 2. Степінь суми двох многочленів не перевищує більшого з степенів даних многочленів: 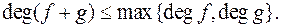
Наслідок 3. Для довільного многочлена 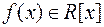 і
і 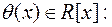
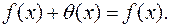
Наслідок 4. Якщо 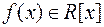 ,
, 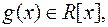 то і
то і 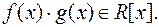
Наслідок 5. Якщо 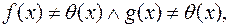 то
то
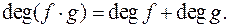
Наслідок 6. 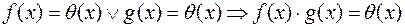 , тобто при множенні двох многочленів, з яких хоч один є нуль-многочленом, дістаємо нуль-многочлен.
, тобто при множенні двох многочленів, з яких хоч один є нуль-многочленом, дістаємо нуль-многочлен.
Теорема про ділення з остачею
Теорема 1.Для будь-яких двох многочленів 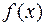 і
і 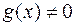 із кільця
із кільця 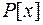 можна знайти в
можна знайти в 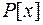 такі многочлени
такі многочлени 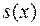 і
і 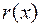 , що
, що
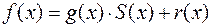 (5),
(5),
при цьому степінь 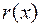 менша за степінь
менша за степінь 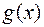 або
або 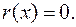 Многочлени
Многочлени 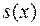 і
і 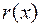 визначаються однозначно.
визначаються однозначно.
Зауваження. Звичайно многочлен 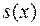 називається неповним часткою від ділення
називається неповним часткою від ділення 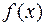 на
на 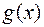 , а многочлен
, а многочлен 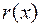 – остачею від ділення
– остачею від ділення 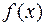 на
на 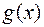 .
.
Означення 7. Многочлен 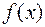 тоді і тільки тоді ділиться на многочлен
тоді і тільки тоді ділиться на многочлен  якщо існує такий многочлен
якщо існує такий многочлен 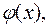 що виконується рівність
що виконується рівність
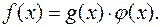 (7)
(7)
Якщо многочлени 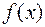 і
і 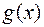 мають раціональні або дійсні коефіцієнти, то і многочлен
мають раціональні або дійсні коефіцієнти, то і многочлен 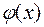 матиме раціональні, або відповідно дійсні коефіцієнти.
матиме раціональні, або відповідно дійсні коефіцієнти.
Властивості подільності многочленів
Відношення подільності многочленів в кільці 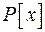 має такі властивості:
має такі властивості:
 .
.
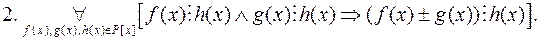
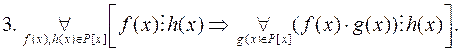
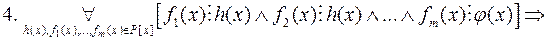
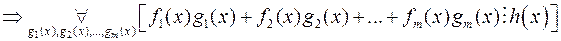
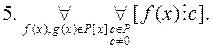
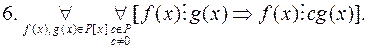
7. Многочлени 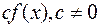 і тільки вони будуть дільниками многочлена
і тільки вони будуть дільниками многочлена 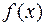 , який має таку ж степінь, як і
, який має таку ж степінь, як і 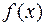 .
.
8.  тоді і тільки тоді, коли
тоді і тільки тоді, коли 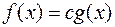 ,
,
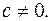
9. Будь-який дільник одного із двох многочленів 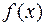 і
і 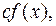 де
де 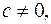 буде дільником і іншого многочлена.
буде дільником і іншого многочлена.
Довільний многочлен 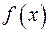 з кільця
з кільця 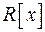 ділиться з остачею на будь-який ненульовий многочлен
ділиться з остачею на будь-який ненульовий многочлен 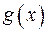 з цього кільця, причому частка i остача визначаються однозначно.
з цього кільця, причому частка i остача визначаються однозначно.
Кільце 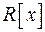 многочленів над довільним полем
многочленів над довільним полем 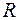 є кільцем головних ідеалів. Кільце
є кільцем головних ідеалів. Кільце 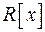 многочленів над полем
многочленів над полем 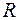 є евклідовим.
є евклідовим.
Алгоритм Евкліда. Найбільший спільний дільник многочленів
Означення 8. Якщо многочлен 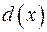 є дільником многочлена
є дільником многочлена 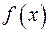 і многочлена
і многочлена 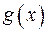 , то він називається спільним дільником многочленів
, то він називається спільним дільником многочленів 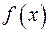 і
і 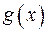 .
.
Означення 9. Спільний дільник многочленів 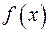 і
і 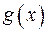 , який ділиться на кожний інший спільний дільник цих многочленів, називається найбільшим спільним дільником многочленів
, який ділиться на кожний інший спільний дільник цих многочленів, називається найбільшим спільним дільником многочленів 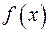 і
і 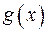 і позначається через
і позначається через 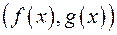 .
.
Найбільший спільний дільник многочленів визначається з точністю до сталого множника однозначно.
Теорема 2.Для будь-яких двох многочленів 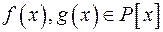 існує найбільший спільний дільник
існує найбільший спільний дільник 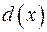 , причому
, причому 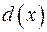 можна подати у вигляді
можна подати у вигляді
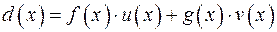 (8)
(8)
Ця теорема не потребує доведення, оскільки випливає з теореми 1.
Наслідок. Многочлени 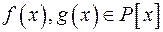 взаємно прості тоді і тільки тоді, коли існують многочлени
взаємно прості тоді і тільки тоді, коли існують многочлени  такі, що
такі, що
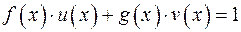 (9)
(9)
З цього наслідку випливають властивості взаємно простих многочленів.
Теорема 3. (Безу) Для будь-якого елемента 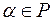 остача при діленні многочлена
остача при діленні многочлена 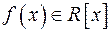 на
на  дорівнює
дорівнює 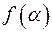 .
.
Властивості взаємно простих многочленів
1. 
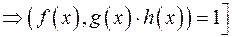 .
.
2. 
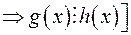 .
.
3. 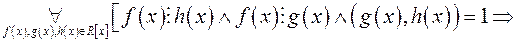
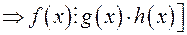 .
.
Означення 10. Спільним кратним многочленів 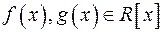 називається будь-який многочлен
називається будь-який многочлен 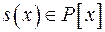 такий, що
такий, що 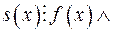
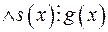 . Найменшим спільним кратним (НСК) многочленів
. Найменшим спільним кратним (НСК) многочленів 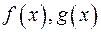 називається спільне кратне
називається спільне кратне 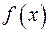 і
і 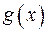 , яке ділить будь-яке інше спільне кратне цих многочленів; НСК многочленів
, яке ділить будь-яке інше спільне кратне цих многочленів; НСК многочленів 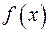 і
і 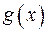 позначають
позначають 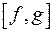 .
.
Теорема 4. Для будь-яких відмінних від нуля многочленів 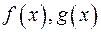 найменше спільне кратне існує і визначається однозначно з точністю до сталого множника.
найменше спільне кратне існує і визначається однозначно з точністю до сталого множника.
Незвідні многочлени
Означення 11.Многочлен 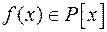 називається незвідним у полі
називається незвідним у полі 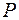 , якщо він не є константа і не має дільників, відмінних від константи і від многочленів виду
, якщо він не є константа і не має дільників, відмінних від константи і від многочленів виду 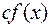 , де
, де 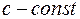 .
.
Означення 12.Многочлен 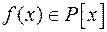 називається звідним у полі
називається звідним у полі 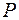 , якщо
, якщо 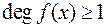 і коли існують такі многочлени
і коли існують такі многочлени 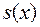 і
і 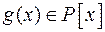 , що
, що 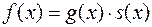 , причому
, причому 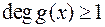 і
і 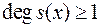 .
.
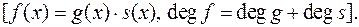
Поняття звідність або незвідність многочлена є поняття відносне і залежить від поля 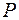 , над яким многочлен розглядається. Будь-який многочлен, який належить
, над яким многочлен розглядається. Будь-який многочлен, який належить 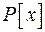 можна вважати також многочленом над полем
можна вважати також многочленом над полем 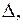 де
де 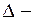 довільне розширення поля
довільне розширення поля 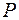 .
.
Якщо 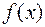 звідний у полі
звідний у полі 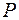 , то він звідний і у будь-якому розширенні цього поля. Але цілком можливо, що многочлен
, то він звідний і у будь-якому розширенні цього поля. Але цілком можливо, що многочлен 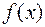 , незвідний у полі
, незвідний у полі 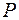 , виявиться звідним у деякому розширенні
, виявиться звідним у деякому розширенні 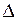 поля
поля 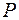 .
.
Теорема5. Многочлен першого степеня над довільним полем 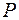 незвідний у цьому полі.
незвідний у цьому полі.
Властивості незвідних многочленів
1. Будь-який многочлен першого степеня незвідний у полі 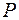 .
.
2. Якщо 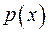 -многочлен, незвідний у даному полі, то і многочлен
-многочлен, незвідний у даному полі, то і многочлен  , де
, де 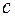 - довільна відмінна від нуля константа, незвідний у цьому полі.
- довільна відмінна від нуля константа, незвідний у цьому полі.
3. Якщо 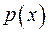 -многочлен, незвідний у даному полі многочлен, а
-многочлен, незвідний у даному полі многочлен, а 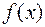 - довільний многочлен над цим полем, то або
- довільний многочлен над цим полем, то або 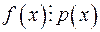 , або
, або  .
.
4. Якщо незвідний у даному полі многочлен 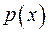 ділиться на інший незвідний у цьому полі многочлен
ділиться на інший незвідний у цьому полі многочлен 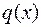 , то ці многочлени збігаються з точністю до сталого множника.
, то ці многочлени збігаються з точністю до сталого множника.
5. Якщо добуток многочленів 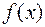 і
і 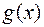 ділиться на незвідний многочлен
ділиться на незвідний многочлен 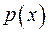 , то хоча б один з цих многочленів ділиться на
, то хоча б один з цих многочленів ділиться на 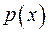 .
.
Канонічний розклад многочлена
Теорема 6. Кожний многочлен 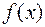 ненульового степеня над полем
ненульового степеня над полем 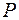 можна подати у вигляді:
можна подати у вигляді:
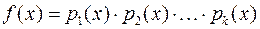 , (13)
, (13)
де всі 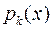 є незвідними многочленами у полі
є незвідними многочленами у полі 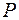 . Зображення (13) єдине з точністю до сталих множників і до порядку нумерації многочленів
. Зображення (13) єдине з точністю до сталих множників і до порядку нумерації многочленів 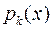 .
.
Наслідок. Довільний многочлен ненульового степеня над полем 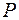 можна подати у вигляді
можна подати у вигляді
 , (18)
, (18)
де 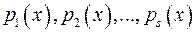 - попарно різні (неасоційовані) многочлени, незвідні у полі
- попарно різні (неасоційовані) многочлени, незвідні у полі 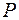 . Це зображення єдине з точністю до сталих множників.
. Це зображення єдине з точністю до сталих множників.
Зображення (18) називають канонічним розкладом многочлена 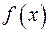 у полі
у полі 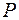 .
.
Означення 13. Якщо многочлен 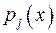 входить у канонічний розклад (180 у степені з показником
входить у канонічний розклад (180 у степені з показником 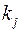 , то кажуть, що
, то кажуть, що 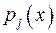 є множником кратності
є множником кратності 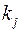 многочлена
многочлена 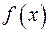 . Множники, кратність яких більша за одиницю, називаються кратними множниками.
. Множники, кратність яких більша за одиницю, називаються кратними множниками.
Теорема 7. Якщо многочлени 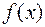 і
і 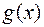 розкладені на незвідні множники у довільному полі
розкладені на незвідні множники у довільному полі 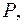 то найбільший спільний дільник
то найбільший спільний дільник 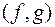 дорівнює добутку всіх незвідних множників, які входять у розклад як
дорівнює добутку всіх незвідних множників, які входять у розклад як 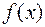 , так і
, так і 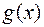 . Якщо таких спільних незвідних множників немає, то
. Якщо таких спільних незвідних множників немає, то 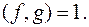
Корені многочленів
Нехай 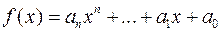 - многочлен над полем
- многочлен над полем 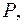 а
а 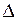 - розширення
- розширення 
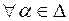 можна обчислити
можна обчислити 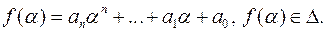
Означення 14.Коренем многочлена 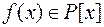 називається елемент
називається елемент 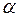 будь-якого розширення
будь-якого розширення 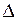 поля
поля 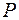 такий, що
такий, що 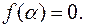
(Корінь многочлена інколи називають нулем многочлена).
Теорема 8. Елемент 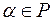 є коренем многочлена
є коренем многочлена 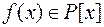 тоді і тільки тоді, коли лінійний двочлен
тоді і тільки тоді, коли лінійний двочлен 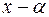 є дільником многочлена
є дільником многочлена 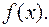
Означення 15. Елемент 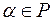 називається коренем многочлена
називається коренем многочлена 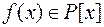 , якщо
, якщо  .
.
Означення 16. Елемент 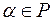 називається
називається 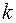 - кратним коренем многочлена
- кратним коренем многочлена 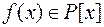 , якщо
, якщо 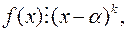 але не ділиться на
але не ділиться на 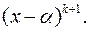
 (19)
(19)
Теорема 9. Число усіх можливих коренів многочлена 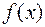 над полем
над полем 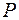 не перевищує його степеня.
не перевищує його степеня.
Наслідок. Якщо многочлен 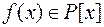 , степінь якого не перевищує
, степінь якого не перевищує 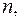 має
має 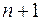 , різних коренів, то
, різних коренів, то 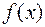 є нуль – многочлен.
є нуль – многочлен.
Теорема 10. Існує один і тільки один многочлен 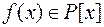 не вище
не вище 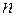 -го степеня, який приймає в
-го степеня, який приймає в 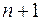 різних точках
різних точках 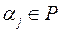 задані значення
задані значення
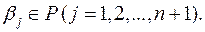
[Доведення дивись Завало С. Т., Костарчук В. М., Хацет Б. І. Алгебра і теорія чисел, ч. 2. – К.: Вища школа, 1976. – 384 с. – стор. 250-251.]
