Критерий Гермейера

Отправляясь от подхода Гермейера к отысканию эффективных и пригодных к компромиссу решений в области полиоптимизации – то есть всех решений, которые не считаются заведомо худшими, чем другие, – можно предложить еще один критерий [4], обладающий в некотором отношении определенной эластичностью. Он с самого начала ориентирован на величины потерь, то есть на отрицательные значения всех е_ij.

В качестве оценочной функции выступает

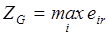, (4.23)

. (4.24)

Сам критерий гласит, таким образом,

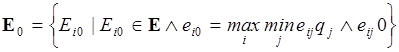. (4.25)

Поскольку в хозяйственных задачах преимущественно имеют дело с ценами и затратами, условие e_ij<0 обычно выполняется. В случае же, когда среди величин e_ij встречаются и положительные значения, можно перейти к строго отрицательным значениям с помощью преобразования е_ij–a при подходящим образом подобранном а>0. (Следует, однако, иметь в виду, что оптимальный вариант решения зависит от а.)

Правило выбора согласно критерию Гермейера (G) формулируется теперь следующим образом:

Матрица решений ||е_ij|| дополняется еще одним столбцом, содержащим в каждой строке наименьшее произведение имеющегося в ней результата на вероятность соответствующего состояния F_j. Выбираются те варианты Е_i0, в строках которых находится наибольшее значение e_ir этого столбца.

В известном отношении G-критерий обобщает ММ-критерий. В случае равномерного распределения 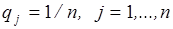они становятся идентичными.

Условия его применимости таковы:

– вероятности появления состояний F_j известны;

– с появлением тех или иных состояний, отдельно или в комплексе, необходимо считаться;

– допускается некоторый риск;

– решение может реализоваться один или много раз.

Если функция распределения известна не очень надежно, а числа реализации малы, то, следуя G-критерию, получают, вообще говоря, неоправданно большой риск. Таким образом, здесь остается некоторая свобода для субъективных действий.