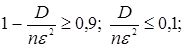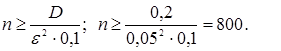Биномиальное распределение. Неравенство Бернулли.

5.1. Схемой Бернулли называют следующую ситуацию: производится n независимых опытов, в каждом из которых может появится событие А с одной и той же вероятностью p.

Вероятность того, что событие А появится k раз вычисляется по формуле

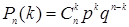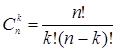, где – число сочетаний из n элементов по k, .

Случайная величина Х, которая принимает целые положительные значения k = 1, 2, …, n с вероятностью 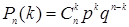, распределена по биномиальному закону (закону Бернулли), ее математическое ожидание 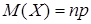, дисперсия ; .

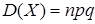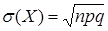5.2. При больших n применяются приближенные формулы

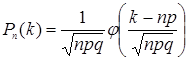– локальная теорема Муавра-Лапласа;

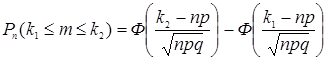– интегральная теорема Муавра-Лапласа. (Значения 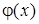и 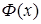см. в таблицах 1,2 в ).

5.3. Связь между относительной частотой появления события А и его вероятностью при распределении Бернулли выражается неравенством 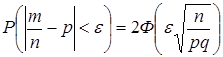, которое называется неравенством Бернулли.

Пример 5.1. Прибор содержит 8 элементов. Каждый из элементов выходит из строя за время Т независимо от других с вероятностью 0,2. Найти вероятность выхода из строя за время работы Т двух элементов.

Решение. В этой задаче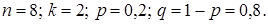

По формуле Бернулли

.

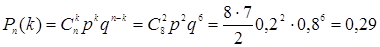Пример 5. 2. Игральную кость бросают 800 раз. Какова вероятность того, что число очков, кратное трем, выпадет а) 267 раз; б) не менее 260 и не более 274 раз.

Решение. Событие А – выпало число очков, кратное трем.

.

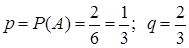а) 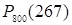будем вычислять по локальной теореме Муавра-Лапласа

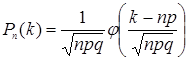; здесь n = 800, k = 267,

;

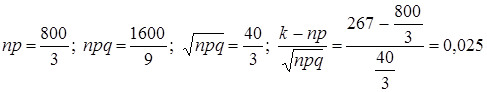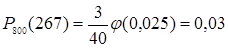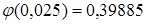, найдено по таблице 1 .

б) Используем интегральную теорему Муавра-Лапласа

, .

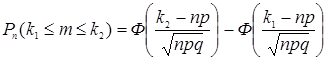
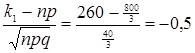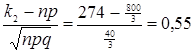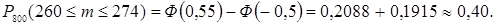
Значение 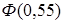и 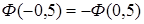найдены по таблице 2 .

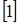Пример 5.3. Вероятность появления события при одном опыте равна 0,3. С какой вероятностью можно утверждать, что частота этого события при 100 опытах будет находиться в пределах от 0,2 до 0,4?

Решение. Связь между частотой события и его вероятностью описывается неравенством Бернулли: 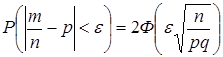, здесь

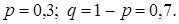Требуется найти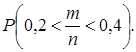

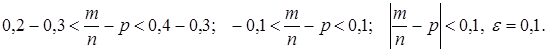
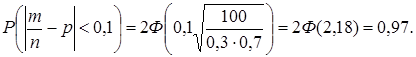
Распределение Пуассона

6.1. Дискретная случайная величина Х, которая принимает только целые неотрицательные значения 0, 1, 2, …, m, … с вероятностями

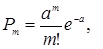(а > 0) называется распределенной по закону Пуассона с параметром а.

Математическое ожидание для этого распределения совпадает с дисперсией и равняется параметру а: .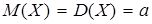

Формулу Пуассона используют как предельную для распределения Бернулли в случае массовых редких явлений (n – велико; p – мало). В этом случае 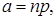(причем ).

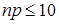6.2. Закон Пуассона хорошо описывает простейший поток при 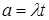. 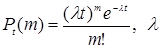– интенсивность потока – среднее число событий в единицу времени; t – время.

Пример 6.1. Радиоаппаратура состоит из 1000 элементов. Вероятность отказа одного элемента в течение одного года работы равна 0,001 и не зависит от состояния других элементов. Какова вероятность отказа двух и не менее двух электроэлементов в год?

Решение. Считая случайное число Х отказавших элементов подчиняющимися закону Пуассона, имеем ,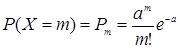

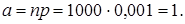
1) Вероятность отказа ровно двух элементов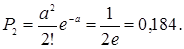

2) Вероятность отказа не менее двух элементов

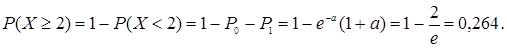
Неравенство Чебышева

7.1. Неравенство Чебышева позволяет оценить близость случайной величины к ее математическому ожиданию:

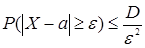или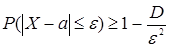

Здесь 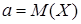– математическое ожидание, 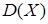– дисперсия случайной величины, 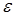– любое действительное число > 0.

7.2. Неравенство Чебышева для частоты случайной величины, распределенной по закону Бернулли, имеет вид

.

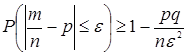Оно дает оценку снизу для отклонения частоты от вероятности при распределении Бернулли. Сравните с неравенством Бернулли! Конечно, эта оценка более грубая, но она легче считается.

7.3. Если имеется n случайных величин 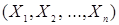, причем

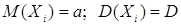для всех i , то для средней 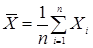справедливо неравенство .

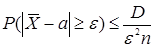7.4. Если математические ожидания у Х_i различные – 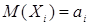, а дисперсия равномерно ограничены числом D , то .

Здесь 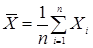– средняя случайных величин; 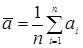– среднее математических ожиданий.

Пример 7. 1. Используя неравенство Чебышева, оценить снизу вероятность того, что при 40000подбрасываниях монеты частота выпадения герба отклонится от вероятности p = 0,5 не более, чем на 0,005.

Решение. Условие задачи позволяет считать, что случайная величина Х – число выпадений герба – имеет распределение Бернулли.

Согласно 7.2. имеем: .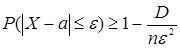

Здесь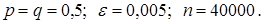

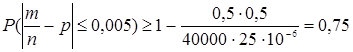, т.е. искомая вероятность не менее 0,75.

Замечание. Эта же вероятность может быть точно найдена с помощью неравенства Бернулли:

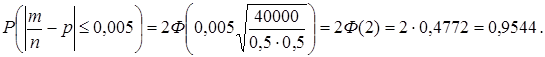
Очевидно, что неравенство Чебышева дает в этом случае очень грубую оценку.

Пример 7. 2. Сколько измерений надо сделать, чтобы их среднее арифметическое дало измеряемую величину с точностью до 0,05 и надежностью 90% если дисперсии случайных величин равны 0,2?

Решение. Связь между средним арифметическим и измеряемой величиной устанавливается неравенством Чебышева:

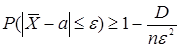. Здесь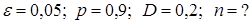

Достаточно n выбрать так, чтобы