Методы решения систем линейных уравнений

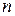Частным случаем системы линейных уравнений с неизвестными вида (2.11) является система 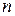линейных уравнений с 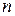неизвестными, т.е. система, в которой число уравнений совпадает с числом переменных:

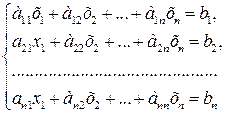(2.15)

Предположим, что определитель матрицы системы (2.15) не равен нулю. Тогда из теоремы Кронекера-Капелли следует, что такая система имеет единственное решение, т.к. .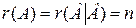

Метод обратной матрицы (матричный метод)

Если матрица коэффициентов системы (2.15) невырожденная 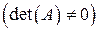, то для нее существует обратная матрица 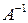. Умножив обе части уравнения (2.13) (где 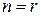) слева на матрицу 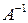, получим

.

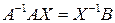Откуда

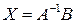(2.16)

Следовательно, если матрица коэффициентов системы (2.15) невырожденная, то система имеет единственное решение, которое можно вычислить по формуле (2.16).

Метод Крамера

Если матрица коэффициентов системы (2.15) невырожденная, то система имеет единственное решение, которое имеет вид:

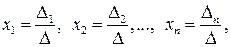(2.17)

где D – определитель матрицы коэффициентов системы и определители , 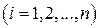получены из определителя D заменой i-го столбца столбцом свободных членов.

Формулы (2.17) называются формулами Крамера.

Рассмотренные выше метод Крамера и метод обратной матрицы могут быть использованы только в случае, когда число уравнений равно числу переменных и матрица коэффициентов системы невырожденная .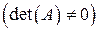

Построение общего решения с помощью формул Крамера

1) Проверить, является ли данная система уравнений совместной.

2) Выбрать один любой ненулевой минор 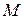матрицы системы уравнений, порядок которого равен рангу матрицы .

3) Выписать все уравнения системы, содержащие строки минора 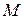. В этих уравнениях в левой части оставить только те переменные, коэффициенты при которых являются столбцами минора 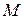, остальные неизвестные переменные перенести в правую часть.

4) Составленную в пункте 3) систему уравнений решить по формулам Крамера (2.17).

Далее будут рассмотрены метод Гаусса и метод Жордана-Гаусса, которые позволяют находить как единственное решение системы уравнений в случае 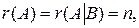так и общее решение в случае .

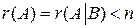Метод Гаусса

Метод Гаусса решения систем линейных уравнений вида (2.11) заключается в последовательном исключении переменных. Согласно этому методу, система уравнений (2.11) с помощью элементарных преобразований приводится к специальному (ступенчатому или треугольному) виду, который позволяет определить неизвестные переменные. После преобразований по методу Гаусса в каждом уравнении системы имеется неизвестная переменная, которая входит в это уравнение с ненулевым коэффициентом, а в последующие уравнения системы эта переменная входит с нулевым коэффициентом.

После того, как система сведена к треугольному (ступенчатому виду) последовательно, начиная с последнего уравнения, находят переменные .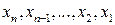

Переход от исходной системы к равносильной системе треугольного или ступенчатого вида называется прямым ходом метода Гаусса. Последовательное нахождение неизвестных переменных из полученной системы уравнений называется обратным ходом метода Гаусса.

Например, если исходная система содержит 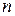уравнений и 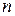переменных и ее определитель 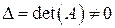, то в результате элементарных преобразований по методу Гаусса будет получена система уравнений, равносильная исходной, вида

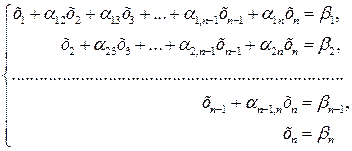(2.18)

Следовательно, в результате прямого хода метода Гаусса исходная система приводится к треугольному виду (2.18). Из системы (2.18) последовательно находим неизвестные переменные (обратный ход метода Гаусса):

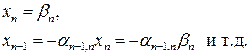
Если исходная система содержит уравнений с 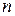неизвестными, то в результате элементарных преобразований система приводится к виду

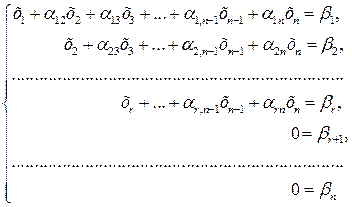(2.19)

Если хотя бы одно из чисел 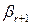,…, в системе (2.19) не равно нулю, то ее последние 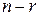уравнений противоречивы и, следовательно, система несовместна. Предположим, что 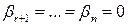, тогда последние 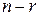уравнений системы (2.19) являются верными равенствами и их можно отбросить. В результате будет получена система, равносильная исходной:

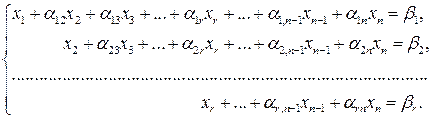(2.20)

Для системы (2.20) возможны два варианта:

1) 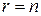. Тогда система (2.20) имеет треугольный вид, совпадающий с (2.18) и существует единственное решение;

2) 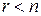. Тогда система (2.20) имеет ступенчатый вид. Существует бесконечное множество решений. При этом значения 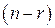переменных (свободных) можно выбрать произвольно, оставшиеся 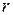переменных выражаются через свободные переменные.

На практике преобразования Гаусса удобнее проводить не с уравнениями системы, а с ее расширенной матрицей.

Метод Жордана – Гаусса

Метод Жордана – Гаусса является модификацией метода Гаусса. В этом случае расширенную матрицу исходной системы приводят к диагональному виду, исключая неизвестные не только из последующих, но и из предыдущих уравнений. После преобразований Жордана-Гаусса в каждом уравнении системы есть переменная, входящая в это уравнение с ненулевым коэффициентом (как правило, равным единице), а в остальные уравнения системы эта переменная входит с нулевым коэффициентом. Следовательно, в результате элементарных преобразований по методу Жордана-Гаусса исходная система уравнений принимает вид

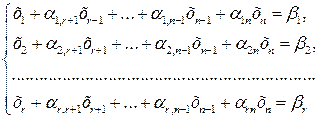(2.21)

Расширенная матрица системы (2.21) есть матрица вида

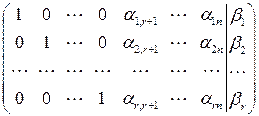
Следовательно, в результате преобразований Жордана-Гаусса необходимо получить 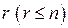единичных столбцов.

Для системы (2.21), как и для системы (2.20), возможны два варианта.

1) Если 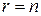, то существует единственное решение. При этом система (2.21) имеет вид

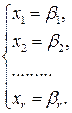
Таким образом, в результате преобразований Жордана-Гаусса сразу получено решение.

2) Если 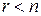, то существует бесконечное множество решений. Оставляем в левой части уравнений системы (2.21) разрешенные переменные, остальные переносим в правую часть:

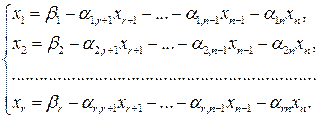(2.22)

В (2.22) переменные 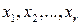являются базисными, переменные – свободными и система (2.22) является общим решением исходной системы. Если в (2.22) свободные переменные приравнять к нулю, то будет получено базисное решение:

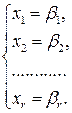
Примеры решения задач

Пример 2.9. Решить систему уравнений

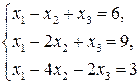
методом Крамера и матричным способом.

Решение. Составим определитель матрицы коэффициентов системы и вычислим его:

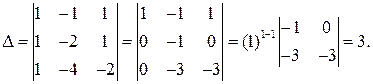
Так как , то данная система имеет единственное решение, которое можно найти по формуле (2.16) или по формулам (2.17).

1. Решим систему методом Крамера. Для этого вычислим определители 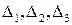, заменяя в определителе 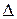соответствующие столбцы столбцом из свободных членов:

, , .

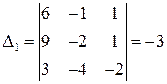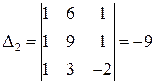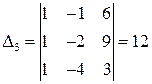Согласно формулам (2.17):

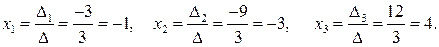
2. Решим систему матричным способом. Так как определитель матрицы системы отличен от нуля, то существует обратная матрица 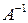. Вычислим алгебраические дополнения и найдем обратную матрицу.

.

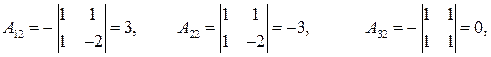
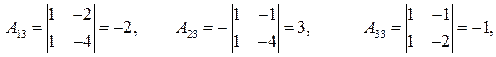
Тогда из (2.16) получаем

Следовательно, .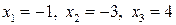

Сделаем проверку. Для этого найденные значения неизвестных переменных подставим во все уравнения исходной системы.

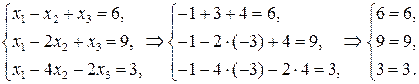
Ответ: .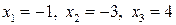

Пример 2.10. Решить систему уравнений

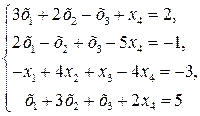
методом Гаусса

Решение. Выписываем расширенную матрицу системы:

.

Приведем расширенную матрицу к ступенчатому виду с помощью элементарных преобразований, выполняемых над ее строками. Для этого последовательно выполним следующие действия:

1. поменяем местами первую и четвертую строки:

;

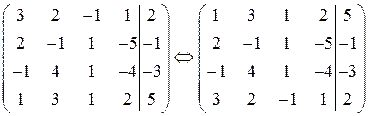2. умножим элементы первой строки на (–2) и прибавим их к соответствующим элементам второй строки:

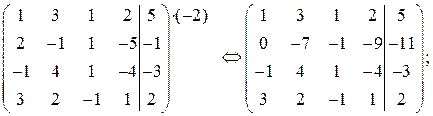
3. к третьей строке прибавим первую строку:

4. умножим элементы первой строки на (–3) и прибавим их к соответствующим элементам четвертой строки:

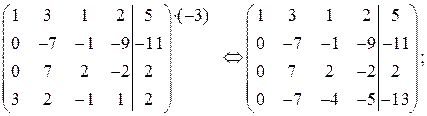
5. элементы второй и четвертой строк умножим на (–1):

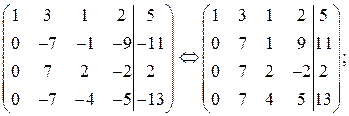
6. от третьей строки отнимем вторую строку:

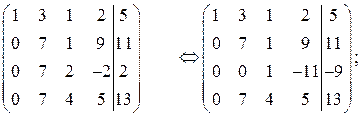
7. от четвертой строки отнимем вторую строку:

8. умножим третью строку на (–3) и прибавим ее к четвертой строке:

;

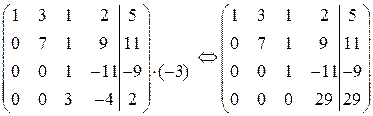9. четвертую строку разделим на 29.

.

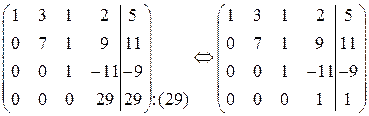Поставим в соответствие полученной расширенной матрице систему, эквивалентную исходной:

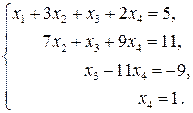(2.25)

Система (2.25) имеет треугольный вид, следовательно, для нее существует единственное решение. Последовательно, начиная с последнего уравнения, находим неизвестные переменные. Из последнего уравнения системы (2.24) видим, что 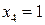. Значение 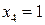подставляем в третье уравнение и находим :

.

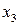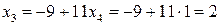Найденные значения переменных 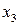и 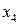подставляем во второе уравнение и находим :

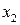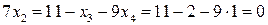или .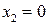

Аналогично из первого уравнения находим :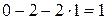

.

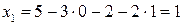Таким образом, решение исходной системы уравнений .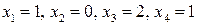

Для проверки правильности решения, подставим полученные значения переменных 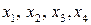в исходную систему уравнений:

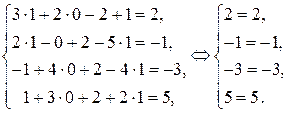
Так как получены верные равенства, то система решена правильно.

Ответ: .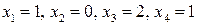

Пример 2.11. Методом Жордана – Гаусса найти решение системы уравнений

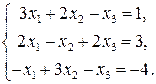
Решение. Выписываем расширенную матрицу системы:

.

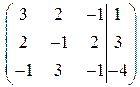С помощью элементарных преобразований расширенной матрицы получим в ней единичные столбцы.

Выбираем первый ведущий элемент. Для упрощения расчетов, как правило, в качестве такого ведущего элемента берут элемент 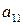, предварительно преобразовав матрицу так, чтобы 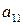был равен единице. В нашем примере для этого третью строку матрицы умножим на ( 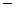1) и поменяем ее местами с первой строкой.

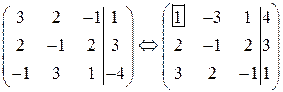
В новой матрице умножим первую строку на (–2) и прибавим ко второй строке, затем умножим первую строку на (–3) и прибавим к третьей строке:

.

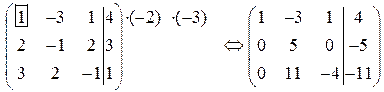В результате преобразований получен один единичный столбец – первый столбец матрицы.

Разделим вторую строку на пять, тем самым получив еще один ведущий элемент 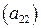, но уже во втором столбце:

.

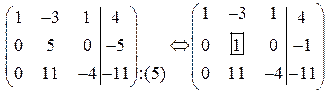В последней матрице умножим вторую строку на (–11) и прибавим ее к третьей строке. Вторую строку умножим на три и прибавим к первой строке.

.

Теперь третью строку разделим на (–4) и отнимем ее от первой строки:

.

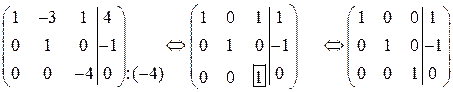Число единичных столбцов равно числу переменных, следовательно, система имеет единственное решение – .

Непосредственная подстановка найденных значений в уравнения исходной системы подтверждает правильность вычислений.

Ответ: .

Для систем с большим числом уравнений метод Жордана – Гаусса удобно реализовывать в виде таблицы, которую называют таблицей Гаусса, каждый ее блок содержит результат одного преобразования или одной итерации.

Пример 2.12.Решить линейную систему уравнений

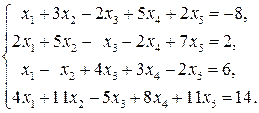
Решение. Составляем первую таблицу Гаусса. В первые столбцы вносим коэффициенты при неизвестных переменных и свободные члены. В таблицу добавлены два дополнительных столбца – «сумма» и «проверка». В столбец «сумма» будем записывать сумму всех коэффициентов и свободного члена соответствующей строки таблицы. Столбец «контроль» необходим для проверки правильности вычислений. В первом блоке таблицы этот столбец совпадает со столбцом «сумма». Элементарные преобразования будут проводиться не только со столбцами расширенной матрицы, но и с контрольным столбцом.

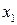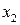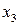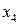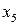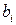						контроль	сумма
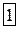		–2			–8
		–1	–2
	–1			–2
		–5			–14

1. В качестве ведущего элемента выбираем 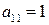(в таблице он выделен). В новую таблицу переписываем без изменения строку, содержащую единичный ведущий элемент. С помощью элементарных преобразований получаем единичный столбец. Для этого выполняем такие преобразования:

1) переписываем без изменения первую строку, содержащую единичный ведущий элемент;

2) первую строку, умноженную на 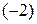прибавляем ко второй строке;

3) первую строку прибавляем к третьей строке;

4) первую строку, умноженную на , прибавляем к четвертой строке.

Получаем второй блок таблицы:

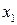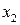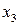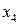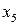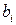						контроль	сумма
		–2			–8
	–1		–12
	–4		–2	–4
	–1		–12

Так как сумма элементов каждой строки равна соответствующему контрольному значению, то вычисления верны.

2. Преобразуем в единичный второй столбец. Ведущий элемент , поэтому ведущую строку предварительно умножим на .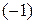

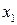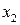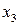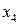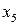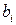						контроль	сумма
		-2			-8
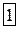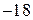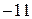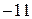	–4		–2	–4
	–1		–12

Далее проводим следующие элементарные преобразования:

1) вторую строку, содержащую единичный ведущий элемент переписываем без изменения;

2) вторую строку, умноженную на 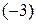, прибавляем к первой строке;

3) вторую строку, умноженную на 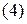, прибавляем к третьей строке;

4) вторую строку прибавляем к четвертой строке.

Получаем третий блок таблицы:

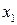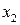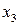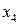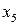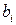						контроль	сумма
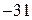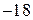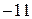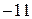		–6		–16	–58	–34	–34

3. Последняя строка дает тривиальное уравнение, его можно удалить.

Следующий ведущий элемент должен стоять в третьей строке. Разделим все элементы третьей строки на :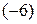

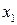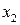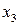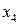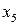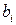						контроль	сумма

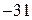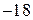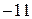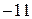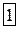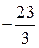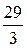Проводим следующие элементарные преобразования:

1) третью строку, содержащую единичный ведущий элемент, переписываем без изменения;

2) третью строку, умноженную на 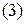, прибавляем ко второй строке;

3) третью строку, умноженную на 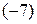, прибавляем к первой строке.

Получаем четвертый блок таблицы:

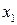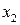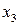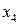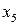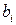						контроль	сумма

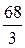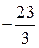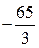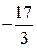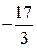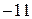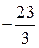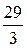Число единичных векторов равно числу строк таблицы (уравнений системы), следовательно, преобразования закончены.

Из последнего блока таблицы получаем систему, эквивалентную исходной:

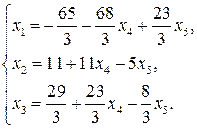
Следовательно, 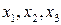– базисные переменные, 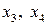– свободные переменные.

Пусть 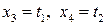, где 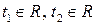– параметры. Тогда общее решение системы уравнений есть система вида

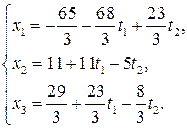
При фиксированных значениях параметров из общего решения получаем частное. Например, при 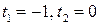будет получено частное решение .

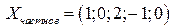Базисное решение получаем из общего, полагая : .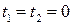

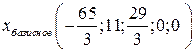Ответ: .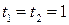

Пример 2.14. Найти методом Жордана – Гаусса общее решение и одно частное решение системы

Решение. Выпишем расширенную матрицу системы:

.

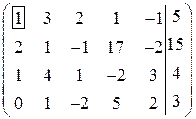Первое уравнение не содержит разрешенной переменной. Переменная 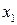входит в это уравнение с коэффициентом единица. Исключим 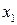из других уравнений с помощью элементарных преобразований:

.

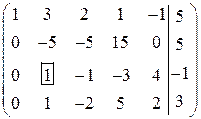В полученной системе ни одно уравнение кроме первого, не содержит разрешенного неизвестного. Третье уравнение содержит переменную 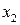с коэффициентом единица. С помощью элементарных преобразований исключим переменную 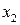из остальных уравнений:

.

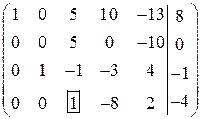В четвертое уравнение переменная 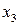входит с коэффициентом единица. С помощью элементарных преобразований исключим переменную 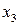из остальных уравнений:

.

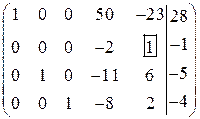Полученная система не является разрешенной, т.к. второе уравнение не содержит разрешенного неизвестного. С помощью элементарных преобразований исключим переменную 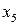из первого, третьего и четвертого уравнений:

.

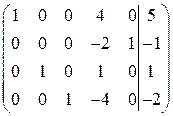В результате получена разрешенная система вида

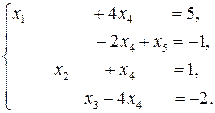
В этой системе 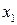, , 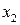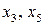– разрешенные (базисные) переменные, 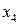– свободная переменная. Общее решение исходной системы уравнений имеет вид:

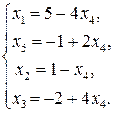
Пусть, например, 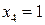. Тогда , , 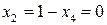, 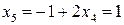. Следовательно, 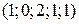– частное решение системы уравнений.

Пример 2.15. Найти все базисные решения системы

Решение. Находим общее решение системы, преобразовав расширенную матрицу системы:

.

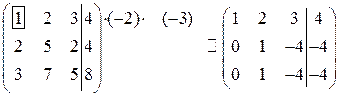Так как две последние строки совпадают, то одну можно удалить:

.

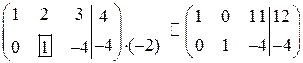Единичные столбцы соответствуют переменным 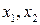, которые являются в данном случае базисными. Из последней матрицы

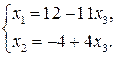
Приравнивая свободные переменные к нулю, находим первое базисное решение: .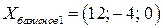

Выбираем теперь в качестве базисных переменные 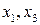. Для этого переменную 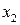выводим из базиса, а переменную 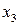вводим:

.

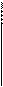
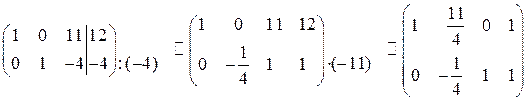Отсюда ,.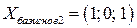

Теперь в качестве базисных берем переменные 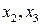. Для этого переменную 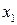выводим из базиса, а переменную 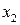опять вводим в базис:

.

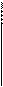
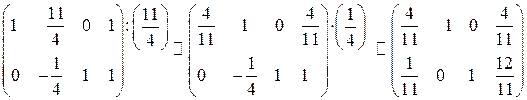Отсюда .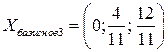

Число найденных базисных решений .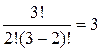

Ответ. , , .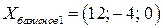

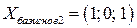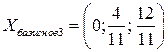Вопросы для самопроверки

2.19. Какая система уравнений называется совместной? несовместной?

2.20. Какая система уравнений называется определенной? неопределенной?

2.21. Запишите линейную систему уравнений в матричном виде.

2.22. Сформулируйте теорему Кронекера – Капелли.

2.23. При каком условии система линейных уравнений имеет единственное решение?

2.24. Какой вид имеют формулы Крамера?

2.25. Как решить систему уравнений матричным способом?

2.26. В чем состоит принцип метода Гаусса?

2.27. Что называется прямым и обратным ходом метода Гаусса?

2.28. В чем состоит принцип метода Жордана – Гаусса?

2.29. Какая система уравнений называется разрешенной?

2.30. Что такое общее решение системы линейных уравнений?

2.31. Как из общего решения системы уравнений получить частное решение?

2.32. Что такое базисное решение?