Задача №2. Расчет вала на прочность и жесткость при кручении
Дано:К стальному валу кольцевого поперечного сечения с жесткой заделкой на одном конце приложены три внешних момента относительно продольной оси OX (рисунок 4.7).
Значения двух моментов заданы: M1=0,4кН·м, M2=2,0кН·м. Линейные размеры вала равны: а=b=c=1м. Отношение внутреннего и наружного диаметров сечения K=d/D=0,8; допускаемое касательное напряжение [τ]=40МПа; допускаемый относительный угол закручивания [θ]=0,5град/м, модуль сдвига стали G=0,8·105 МПа.
Требуется:
1) установить, при каком значении момента M3 исключается поворот свободного торцевого сечения.
2) определить величины крутящих моментов по участкам с учетом найденного значения M3 и построить их эпюры.
3) подобрать размеры кольцевого сечения по условиям прочности и жесткости вала.
Решение:
1. По исходным данным составляется расчетная схема вала с соблюдением масштаба (рисунок 4.2а).
2. Определяется неизвестный момент пары сил в концевом сечении.
Полагаем момент М3 положительным и известным М3=МХ.
Выделяем три расчетных участка, границами которых являются сечения, где появляется нагрузка (на рисунке участки KC, СВ и ВА. В пределах каждого проводится произвольное сечение.
| Рисунок 4.1 |
Определение неизвестного момента М3
Рассматривая от каждого сечения правую отсеченную часть (так как там нет опоры), вычисляем величины крутящих моментов, используя следующее рабочее правило, вытекающее из метода сечений:
Крутящий момент в любом сечении бруса численно равен алгебраической сумме моментов всех внешних сил, действующих по одну сторону от сечения относительно продольной оси бруса в месте сечения.
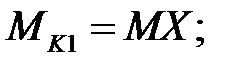
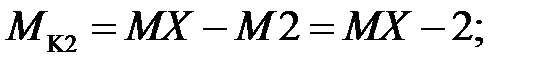
(пример определения MK2 представлен на рисунке 4.2, г)
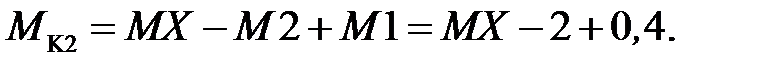
Эти значения моментов по расчетным участкам представлены на рисунке 4.2, б.
Угол закручивания i-го расчетного участка при постоянных характеристиках материала, сечения и нагрузки определяется по формуле:
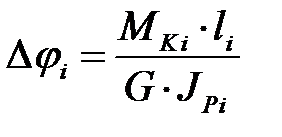 .
.
Сечение А в зоне заделки не закручивается. Перемещаясь по сечениям от зоны заделки вправо к свободному концу, имеем: 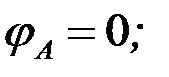
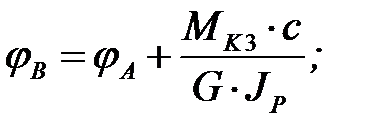
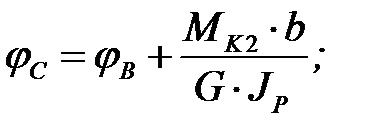
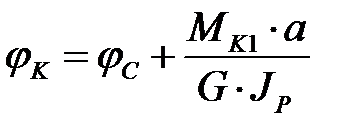 .
.
После подстановки известных значений и при условии, что поворот в торцевом сечении исключен (угол поворота равен нулю) получаем:
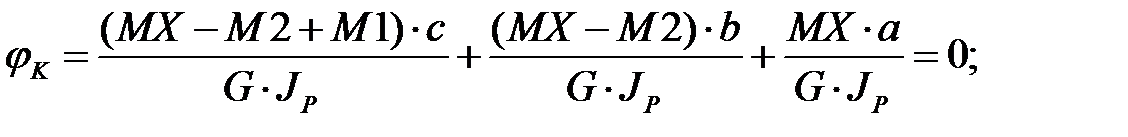
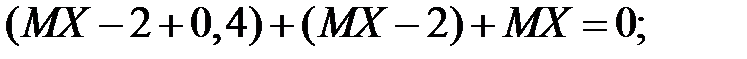
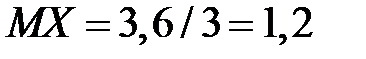 кН· м.
кН· м.
Определение величины крутящих моментов по участкам
Величины крутящих моментов по участкам вычисляем, используя рабочее правило метода сечений:
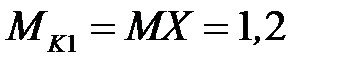 кН· м,
кН· м,
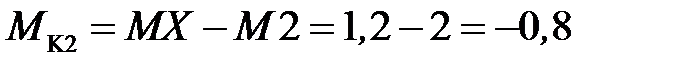 кН· м,
кН· м,
(пример определения MK2 представлен на рисунке 4.2, г)
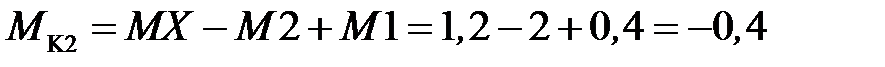 кН· м.
кН· м.
По этим значениям строим эпюры МК (см. рисунок 4.2, д).
Откуда получаем: 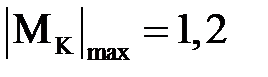 кН· м.
кН· м.
Подбор сечения по условию прочности
Определяется требуемый полярный момент сопротивления по условию прочности:
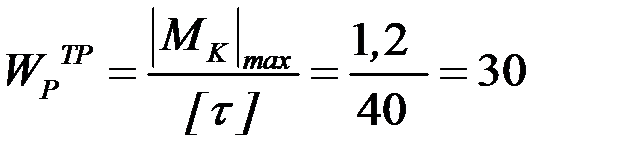 см3.
см3.
Полярный момент сопротивления для бруса кольцевого сечения равен: 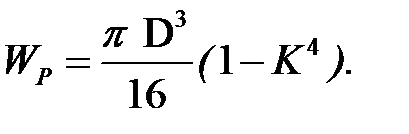
Приравниваем 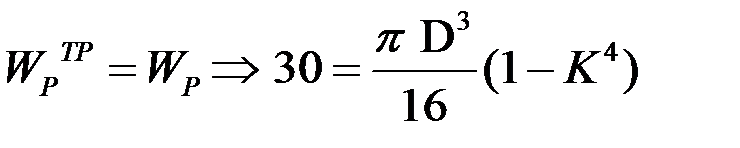 см3 .
см3 .
Отсюда при заданном К = 0,8 находим D = 6,37 см.
Подбор сечения по условию жесткости
Из условия жесткости 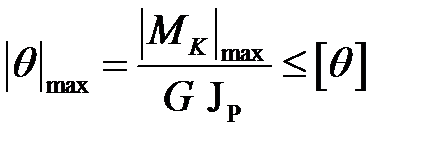 определяется требуемое значение полярного момента инерции по следующей формуле:
определяется требуемое значение полярного момента инерции по следующей формуле:
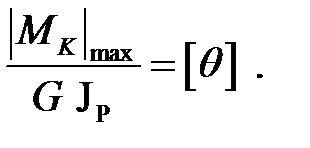
Откуда, 
В это соотношение 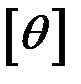 подставляется в радианах, поэтому заданный угол выразим в радианах:
подставляется в радианах, поэтому заданный угол выразим в радианах:
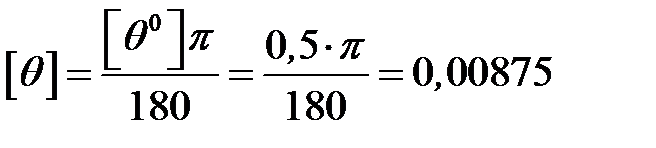 рад/м,
рад/м,
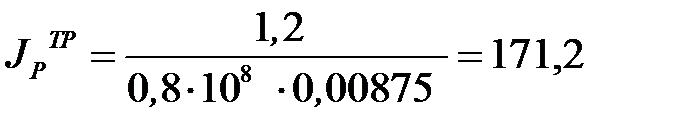 см4.
см4.
Из условия 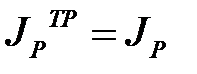 получим:
получим: 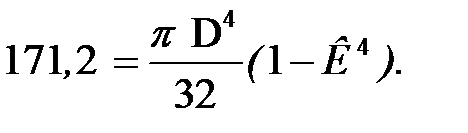
Отсюда, определяем D (по условию задачи К = 0,8):
 см.
см.
После округления примем D = 7,4 см, тогда,
d = 0,8 ×D = 0,8 × 7,4 = 5,92 см.
По результатам расчетов на прочность и жесткость видно, что по условию жесткости диаметр бруса требуется больше, чем по условию прочности (7,4 см > 6,37 см).
Окончательно принимаем больший диаметр:
D = 7,4 см, d = 5,92 см.
Рисунок 4.2
Проверка прочности и жесткости подобранного сечения
Предварительно определим полярный момент сопротивления и полярный момент инерции подобранного сечения:
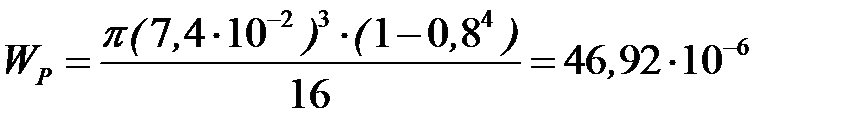 м3,
м3,
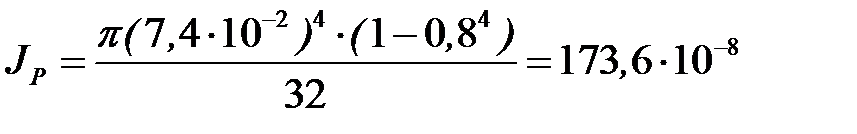 м4 ,
м4 ,
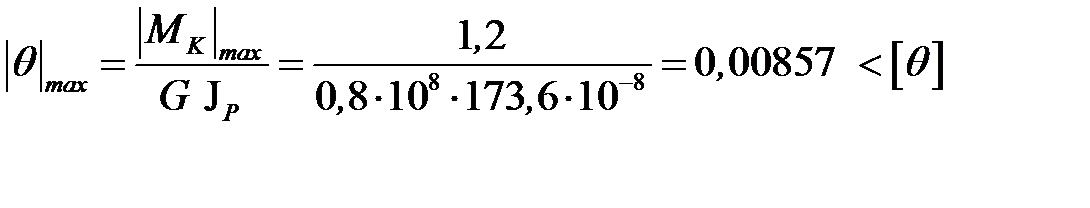 ,
,
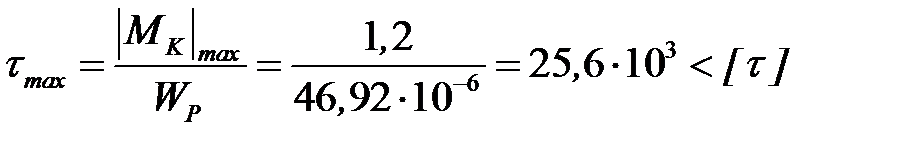 МПа.
МПа.
Условия прочности и жесткости выполняются.
Расчет вала круглого поперечного сечения производится аналогично, начиная с п.4.
Эпюра углов закручивания строится аналогично эпюре перемещений в задаче 1.1.
| № | M1 | M2 | a | b | c |
| 0,8 | 2.0 | 1,0 | 1,1 | 1,2 | |
| 0,3 | 2,1 | 1,1 | 1,2 | 1,3 | |
| 0,8 | 2,2 | 1,2 | 1,3 | 1,4 | |
| 0,9 | 2,3 | 1,3 | 1,4 | 1,5 | |
| 0,5 | 2,4 | 1,4 | 1,5 | 1,6 | |
| 0,4 | 2,5 | 1,5 | 1,6 | 1,7 | |
| 0,8 | 2,6 | 1,6 | 1,7 | 1,8 | |
| 0,6 | 2,7 | 1,7 | 1,8 | 1,9 | |
| 0,5 | 2,8 | 1,8 | 1,9 | 2,0 | |
| 0,8 | 2,8 | 1,9 | 2,0 | 1,9 | |
| 0,7 | 2,9 | 2,0 | 1,9 | 1,8 | |
| 0,6 | 3,0 | 1,9 | 1,8 | 1,7 | |
| 0,5 | 2,9 | 1,8 | 1,7 | 1,6 | |
| 1,0 | 2,8 | 1,7 | 1,6 | 1,5 | |
| 0,9 | 2,7 | 1,6 | 1,5 | 1,4 | |
| 0,8 | 2,6 | 1,5 | 1,4 | 1,3 | |
| 0,7 | 2,5 | 1,4 | 1,3 | 1,2 | |
| 0,6 | 2,4 | 1,3 | 1,2 | 1,2 | |
| 0,5 | 2,3 | 1,2 | 1,1 | 1,1 | |
| 0,4 | 2,2 | 1,1 | 1,0 | 1,0 |
Вопросы для письменного ответа
1. Как определяется внутренний крутящий момент в поперечном сечении вала? Какое принято правило знаков для крутящего момента?
2. Как записывается условие прочности вала при кручении?
3. Что такое относительный угол закручивания? Как он вычисляется и какова его размерность?
4. Как формулируется условие жёсткости для вала?
Варианты тестовых заданий
| 4.1 | Чему равен наибольший по модулю крутящий момент? | |
| 4.2 | Чему равен крутящий момент на участке 3? | |
| 4.3 | Чему равен неизвестный крутящий момент? | |
| 4.4 | На каком участке вала деформация наибольшая, если размеры их считать одинаковыми? | |
| 4.5 | На каком участке вала деформация наименьшая, если размеры их считать одинаковыми? | |
| 4.6 | Укажите правильное распределение напряжений при кручении круглого вала. | |
| 4.7 | Укажите вариант рационального распределения моментов на валу. | |
| 4.8 | Укажите номер точки, где касательное напряжение при кручении наибольшее. | |
| 4.9 | Расположите номера точек в порядке убывания касательных напряжений при кручении. |
