Классы смежности по нормальной подгруппе и факторгруппа
Предложение 1. Пусть  - нормальная подгруппа группы
- нормальная подгруппа группы  и
и 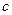 -какой-либо элемент
-какой-либо элемент  . Тогда
. Тогда  .
.
Доказательство. По определению нормальной подгруппы 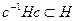 . Тогда
. Тогда 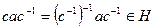 и
и 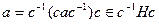 . Поэтому
. Поэтому 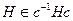 и, следовательно,
и, следовательно,  .
.
Предложение 2. Если  - нормальная подгруппа группы
- нормальная подгруппа группы  и
и 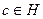 , то
, то 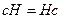 .
.
Доказательство. Согласно предыдущему предложению  . Умножив это равенство слева на
. Умножив это равенство слева на 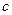 , получим требуемое равенство.
, получим требуемое равенство.
Предложение 3. Классы смежности по нормальной подгруппе образуют группу относительно умножения подмножеств группы. Единицей этой группы является сама подгруппа.
Доказательство. Пусть  - группа и
- группа и  - ее нормальная подгруппа. Рассмотрим произведение двух классов смежности
- ее нормальная подгруппа. Рассмотрим произведение двух классов смежности 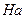 и
и 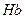 . Воспользуемся ассоциативностью умножения подмножеств и предложением 2. Имеем:
. Воспользуемся ассоциативностью умножения подмножеств и предложением 2. Имеем: 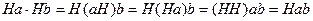 , т. е. произведение двух классов смежности оказалось классом смежности. Далее,
, т. е. произведение двух классов смежности оказалось классом смежности. Далее, 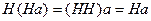 и
и 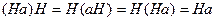 , так что
, так что  есть единица при этом умножении. Осталось рассмотреть наличие обратного элемента:
есть единица при этом умножении. Осталось рассмотреть наличие обратного элемента: 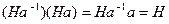 и
и 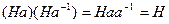 . Следовательно,
. Следовательно,  есть обратный элемент для
есть обратный элемент для 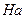 .
.
Определение. Группа, образованная классами смежности группы  по нормальной подгруппе
по нормальной подгруппе  называется факторгруппой
называется факторгруппой  по
по  и обозначается
и обозначается 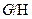 .
.
Определение факторгруппы можно сформулировать в терминах сравнения. Назовем два элемента 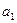 и
и  сравнимыми по нормальной подгруппе
сравнимыми по нормальной подгруппе  , если
, если 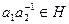 или, что то же самое,
или, что то же самое, 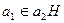 , т. е.
, т. е. 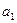 и
и  принадлежат одному классу смежности по
принадлежат одному классу смежности по  . Тогда, если
. Тогда, если 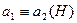 и
и 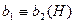 , то
, то 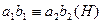 , так как
, так как 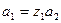 ,
, 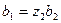 и
и 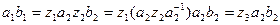 при
при 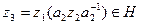 , т. е.
, т. е. 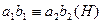 .Поэтому, если определить произведение классов как класс, содержащий произведение каких-либо представителей этих классов, определение будет корректным. Оно совпадает с определением произведения классов смежности как элементов факторгруппы.
.Поэтому, если определить произведение классов как класс, содержащий произведение каких-либо представителей этих классов, определение будет корректным. Оно совпадает с определением произведения классов смежности как элементов факторгруппы.
