Классы смежности

Определение. Множество 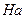, где - подгруппа группы , 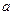- некоторый элемент из , называется левым классом смежности группы по подгруппе .

Между элементами подгруппы и элементами левого класса смежности 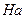имеется взаимно однозначное соответствие: 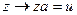, 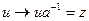. Если подгруппа конечна, то число элементов в каждом левом классе смежности равно порядку .

Теорема 1. Два левых класса смежности группы по подгруппе либо совпадают, либо не имеют общих элементов.

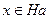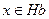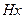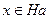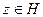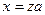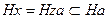Доказательство. Сначала докажем, что если два левых класса смежности имеют общий элемент, то они совпадают. Пусть и . Рассмотрим класс смежности . Так как , то при некотором выполняется равенство и . Но 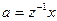, поэтому 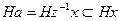. Следовательно, 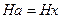. Аналогично 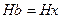, так что 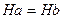. Теорема доказана.

При доказательстве этой теоремы выяснилось, что 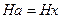при любом 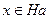, т. е. в качестве элемента, порождающего как правый множитель класс смежности, можно взять любой элемент из этого класса.

Определение. Дизъюнктивным объединением называется объединение множеств, попарно не имеющих общих элементов.

Теорема 2. Группа является дизъюнктивным объединением классов смежности по подгруппе.

Доказательство. Любой элемент группы 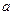принадлежит некоторому классу смежности, именно 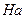, а различные классы не имеют общих элементов. Теорема доказана.

Определение. Разбиение группы на левые классы смежности, не имеющие общих элементов, называется разложением группы по подгруппе.

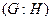Если число левых классов смежности в разложении группы по подгруппе конечно, то это число называется индексом подгруппы в группе и обозначается . Очевидно, что если группа конечна, то индекс любой ее подгруппы конечен.

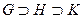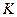Теорема 3. Пусть , причем и - подгруппы в . Если в имеет конечный индекс и 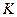в имеет конечный индекс, то 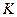в имеет конечный индекс и .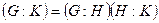

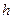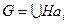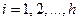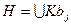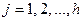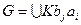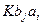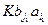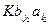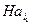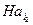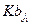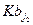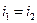Доказательство. Пусть индекс подгруппы в группе равен , т. е. разложение по имеет вид: , и , . Тогда . Нужно показать, что классы смежности попарно не имеют общих элементов. Если и содержат общий элемент, то и , потому что и содержатся в . Следовательно, . Но в этом случае 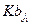= 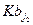, что возможно только при 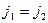. Итак, есть дизъюнктивное объединение классов смежности 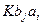. Их число равно 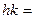= 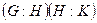, т. е. 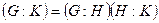. Теорема доказана.

Если подгруппа состоит только из одного единичного элемента, то классами смежности являются одноэлементные множества из элементов группы, поэтому индекс 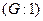равен порядку группы .

Теорема Лагранжа. Во всякой конечной группе порядок ее подгруппы является делителем порядка самой группы.

Доказательство. Доказательство следует непосредственно из предыдущей теоремы, если рассмотреть: 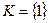, то 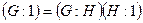. Таким образом, порядок группы делится на порядок ее подгруппы и частное от их деления равно индексу в . Теорема доказана.

Наряду с левыми классами смежности можно рассматривать правые классы смежности 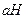. Для них также справедлива теорема о разложении группы по подгруппе.

Между левыми и правыми классами смежности имеется взаимно однозначное соответствие: отображение 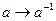есть взаимно однозначное отображение группы на себя и это отображение переводит левые классы смежности в правые. Действительно, левый класс смежности 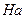состоит из элементов 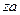( 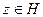) и обратные элементы 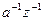заполняют правый класс смежности 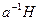. Поэтому если для группы имеется конечное число левых классов смежности, то столько же будет и правых, так что определение индекса подгруппы при помощи левых и правых классов смежности дает одно и то же.