Дії над комплексними числами, заданими в алгебраїчній формі.

Скалярний добуток векторів та його властивості.

Скалярним добутком двох ненульових векторів називається число, яке дорівнює добутку довжин цих векторів на косинус кута між ними.

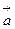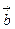Скалярний добуток векторів і позначають символом 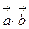. Отже, за означенням

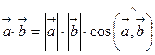
Скалярний добуток двох векторів дорівнює модулю одного з них, помноженому на проекцію другого вектора на напрям першого:

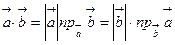
Наведемо такі властивості скалярного добутку:

1. 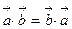(властивість переставності).

2. 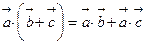(властивість розподільності).

3. 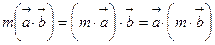(властивість сполучності).

№№№№№№

Вектор простору має таку властивості:

1) вектор є переміщення; 2) вектор відображає промінь на співнапрямлений з ним промінь, пряму – на паралельну їй пряму, площину – на паралельну їй площину.

Правила дій над векторами, заданими своїми координатами.

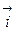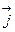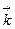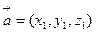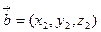Якщо в базисі ( , , ) задано вектори і , то:

- координати суми двох (або більше) векторів дорівнюють сумам відповідних координат доданків, тобто

;

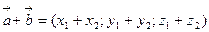- координати різниці двох векторів дорівнюють різницям відповідних координат цих векторів, тобто

;

- координати добутку вектора на число дорівнюють добуткам відповідних координат даного вектора на це число:

.

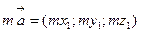У просторі. Довжину вектора 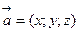(відстань між двома точками) обчислюють за формулою

.

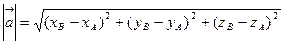Довжину радіус-вектора 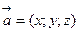обчислюють за формулою

.

№№№№

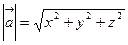Означення 1. Комплексними числами називаються числа виду а+ві, де а і в - дійсні числа, а уявна одиниця і визначається рівністю і² = -1 .

Запис комплексного числа у вигляді z = а+ві називається алгебраїчною формою комплексного числа. Дійсне число а називається дійсною частиною комплексного числа z = а+ві, а вираз ві- уявною частиною, дійсне число в – коефіцієнтом при уявній частині. Комплексне числ а-ві називається коплексно-спряженим із числом а+ві.

Означення 2. Модулем комплексного числа z = а+ві називається число

|z| = | а+ві | =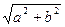

Модуль комплексного числа зажди є дійсне невід’ємне число: |z| ≥ 0, причому |z| = 0 тоді і тільки тоді, коли z = 0.

Означення 3. Кут φ між дійною віссю Ох і вектором ОМ, який відлічують від додатного напрямку дійсної осі, називається аргументом комплексного числа z ≠ 0.

Зображення комплексного числа у вигляді z = r(cosφ + isinφ), де r >0, називається тригонометричною формою комплексного числа.

Зображення комплексного числа у вигляді z = r℮^φі, де r >0, називається показниковою формою комплексного числа.

№№№№

Дії над комплексними числами, заданими в алгебраїчній формі.

- сумою двох комплексних чисел 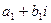і 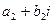називається комплексне число ;

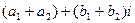- добутком двох комплексних чисел 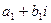і 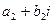називається комплексне число ;

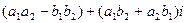- щоб виконати ділення двох комплексних чисел, ділене і дільник множать на комплексне число, спряжене дільнику.

№№№№