Формулы Крамера для решения системы линейных

уравнений

Рассмотрим случай, когда число уравнений системы совпадает с числом неизвестных (т.н. квадратная система):

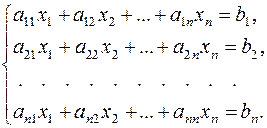(1)

Матрицу, составленную из коэффициентов системы (1), А=(а_ij), называют основной матрицей системы, а её определитель Δ=det(A) называют определителем системы.

Теорема. Квадратная система (1) с отличным от нуля определителем имеет решение, и притом, единственное. Его можно найти по формулам

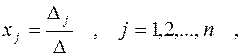(2)

где Δ_j – это определитель, получающийся из определителя Δ после замены в нем j-го столбца столбцом свободных членов системы (1).

Доказательство. Докажем сначала, что числа, определяемые формулами (2), дают решение системы (1). Возьмём левую часть i-го уравнения системы и подставим в нее эти числа, при этом определитель Δ_j разложим по j-му столбцу:

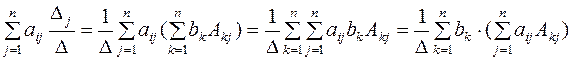
Внутренняя сумма 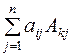(т.е. множитель, стоящий возле b_k) в полученном выражении либо равна определителюΔ, если k=i, либо равна 0, если k≠j. Значит во внешней сумме только i-е слагаемое отлично от нуля и вся эта сумма равна b_i·Δ. Откуда получаем, что левая часть i-го уравнения при подстановке (2) равна 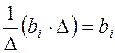, т.е. правой части этого уравнения. Итак, числа (2) дают решение системы (1).

Докажем теперь единственность решения (2), для чего предположим, что существуют числа с₁,с₂,…,с_n такие, что:

(3)

есть система верных числовых равенств. Выполним с этими верными равенствами следующее: 1^е умножим на алгебраическое дополнение элемента а₁₁, 2^е – на дополнение элемента а₂₁ и т.д. и почленно сложим. Получим следующее:

(a₁₁A₁₁+a₂₁A₂₁+…+a_n1A_n1)c₁+(a₁₂A₁₁+a₂₂A₂₁+…+a_n2A_n1)c₂+…

…+(a_1nA₁₁+a_2nA₂₁+…+a_nnA_n1)c_n=b₁A₁₁+b₂A₂₁+…+b_nA_n1.

Первая скобка в левой части равна определителю Δ, а все остальные скобки равны 0. Правая же часть есть разложение определителя Δ₁ по первому столбцу. Итак, мы получили

Δ·с₁ = Δ₁.

Если же указанную процедуру повторить, взяв в качестве множителей алгебраические дополнения элементов а₁₂, а₂₂,…,а_n2, то получим

Δ·с₂ = Δ₂

и так далее по аналогии Δ·с_n= Δ_n. Поскольку по условию Δ≠0, то полученные равенства эквивалентны соотношениям

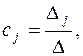
что и означает, что у системы (1) нет других решений кроме тех, что даются формулами Крамера. Теорема доказана.

Значение формул Крамера заключается главным образом в том, что в тех случаях, когда они применимы, эти формулы дают явное выражение для решения системы через коэффициенты и свободные члены. Практическое использование формул Крамера связано с довольно громоздкими вычислениями определителей n-го порядка. К этому следует добавить, что, если коэффициенты уравнений и свободные члены представляют собой лишь приближенные значения каких-либо измеряемых физических величин или округляются в процессе вычислений, то использование формул Крамера может привести к большим ошибкам и в ряде случаев является нецелесообразным.

Замечание. Из полученных в процессе доказательства равенств

c_j·Δ = Δ_j , j=1,2,…,n

следует важный вывод:

если Δ=0, а хотя бы один из Δ₁, Δ₂,…, Δ_n отличен от 0, то системы (1) решений не имеет; в случае же когда Δ=Δ₁=Δ₂=…=Δ_n=0 система (1) может быть или несовместной, или неопределенной.

И еще один полезный вывод из теоремы: если однородная система n уравнений с n неизвестными имеет нетривиальное решение, то её определитель равен 0.