Магнитное поле соленоида и тороида
Соленоид представляет собой провод, плотно навитый на цилиндрический каркас. Линии напряженности магнитного поля соленоида имеют вид, представленный на рис. 3.22 и 3.23.
Формулу (3.48) можно применить для вычисления магнитной индукции поля внутри бесконечного соленоида. В этом случае соленоид удобно рассматривать, как систему круговых витков с общей прямой осью. Силовые линии поля внутри соленоида параллельны его оси, а поле соленоида однородно. Для вычисления циркуляции возьмем прямоугольный контур a-b-c-d (рис. 3.22).
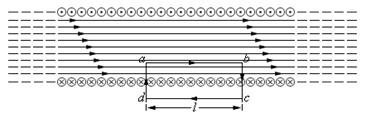
Рис. 3.22 Магнитное поле внутри соленоида
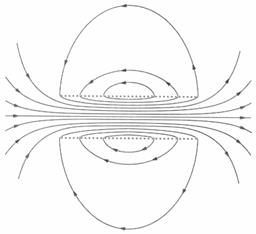
Рис. 3.23 Магнитное поле соленоида
Циркуляцию вектора В по этому контуру можно представить в виде
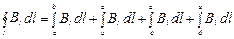, (3.50)
причем
,
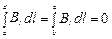так как на этих участках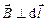 
. Поскольку, соленоид бесконечно длинный, силовые линии, которые проходят внутри него, начинаются в бесконечности и уходят в бесконечность. Поэтому магнитное поле снаружи соленоида отсутствует. Поэтому
.
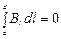Тогда циркуляция вектора 
по замкнутому контуру запишется в виде
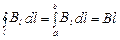, (3.51)
где В ‑ величина магнитной индукции поля в точках расположения отрезка a‑b, а l ‑ длина этого отрезка.
Суммарный ток, охватываемый контуром, Iполн=nlI, где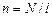 
‑ число витков на единицу длины соленоида, I ‑ сила тока в соленоиде. Тогда, согласно (3.51):
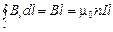. (3.52)
откуда в окончательном виде получается
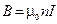. (3.53)
Таким образом, поле бесконечного соленоида однородно, сосредоточено целиком внутри соленоида, а силовые линии вектора магнитной индукции параллельны оси соленоида.
Если мысленно разделить бесконечный соленоид некоторой плоскостью перпендикулярной оси соленоида, то магнитное поле в точках этой плоскости будет создаваться в одинаковой мере обеими половинками соленоида. Если теперь убрать половину соленоида, то у конца полубесконечного соленоида В будет равно:
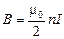. (3.54)
Практически, если длина соленоида значительно больше его диаметра, то формула (3.53) справедлива для средней части соленоида, а формула (3.54) для точек вблизи концов.
Таким образом, магнитное поле уменьшается к краю. Подобный краевой эффект отсутствует у соленоида, свитого в кольцо, так называемого тороида. Его главная особенность состоит в том, что все магнитное поле сосредоточено внутри тороида. Линии вектора магнитной индукции представляют собой замкнутые концентрические окружности (рис. 3.24). Выбирая одну из таких окружностей за контур обхода, и, применяя теорему о циркуляции, легко доказать, что при условии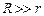 
получается такая же формула, что и для бесконечно длинного соленоида
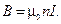
В этом случае поле однородно в каждом из сечений тороида. Но в разных сечениях направлено различно, и имеет смысл говорить об однородности поля в пределах всего тороида только условно, имея в виду только модуль вектора .
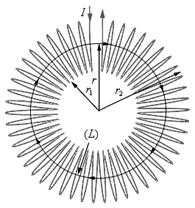
Рис. 3.24 Поле тороида
Используя теорему полного тока, можно получить индукцию магнитного поля на оси тороида, имеющего магнитный сердечник(рис. 3.24)
,
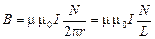где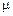 
– магнитная проницаемость сердечника; 
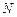– число витков, намотанных на тороид; 
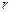– радиус центральной линии тороида.