Проверка статистических гипотез
Статистической гипотезой называется любое предположение о виде или о параметрах неизвестного распределения генеральной совокупности.
Не располагая сведениями обо всей генеральной совокупности, высказанную гипотезу сопоставляют по определенным правилам с выборочными данными и делают вывод о том, можно принять гипотезу или нет. Эта процедура сопоставления называется проверкой гипотезы.
Рассмотрим этапы проверки гипотезы и используемые при этом понятия.
1. Располагая выборочными данными и руководствуясь конкретными условиями рассматриваемой задачи, формулируют гипотезу 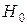 , которую называют основной или нулевой, и гипотезу
, которую называют основной или нулевой, и гипотезу 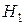 , конкурирующую с гипотезой
, конкурирующую с гипотезой 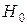 . Гипотезу
. Гипотезу 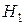 называют также альтернативной, она является логическим отрицанием гипотезы
называют также альтернативной, она является логическим отрицанием гипотезы 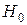 . Выбор тех или иных нулевых или альтернативных гипотез определяется решаемыми исследователем прикладными задачами.
. Выбор тех или иных нулевых или альтернативных гипотез определяется решаемыми исследователем прикладными задачами.
2. Задается вероятность 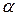 , которую называют уровнем значимости.
, которую называют уровнем значимости.
Уровень значимости 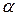 определяет вероятность так называемой ошибки первого рода, которая совершается при отвержении гипотезы
определяет вероятность так называемой ошибки первого рода, которая совершается при отвержении гипотезы 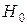 , т.е. принимается конкурирующая гипотеза
, т.е. принимается конкурирующая гипотеза 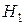 , тогда как на самом деле гипотеза
, тогда как на самом деле гипотеза 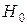 верна. Вероятность
верна. Вероятность 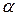 задается заранее малым числом: 0,1; 0,05, 0,001 и т.д.
задается заранее малым числом: 0,1; 0,05, 0,001 и т.д.
3. Выбирается статистический критерий проверки гипотезы – 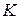 . Статический критерий – это случайная величина, закон распределения которой при условии справедливости проверяемой гипотезы
. Статический критерий – это случайная величина, закон распределения которой при условии справедливости проверяемой гипотезы 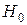 известен.
известен.
После выбора критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при котором нулевая гипотеза отвергается – критическая область 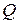 , а другое содержит те значения критерия, при которых гипотеза принимается – область принятия гипотезы. Критическими точками
, а другое содержит те значения критерия, при которых гипотеза принимается – область принятия гипотезы. Критическими точками 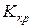 называются точки, отделяющие критическую область от области принятия гипотезы.
называются точки, отделяющие критическую область от области принятия гипотезы.
Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области. Правосторонней (левосторонней)называют критическую область, определяемую неравенством 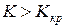 (
( 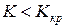 ). Двусторонней называют критическую область, определяемую неравенствами
). Двусторонней называют критическую область, определяемую неравенствами 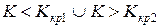 .
.
4. По результатам эксперимента находят эмпирическое (наблюдаемое) значение статистического критерия 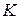 . Если наблюдаемое значение критерия принадлежит критической области, то нулевую гипотезу отвергают в пользу конкурирующей гипотезы; если наблюдаемое значение критерия принадлежит области принятия гипотезы, то нулевую гипотезу принимают.
. Если наблюдаемое значение критерия принадлежит критической области, то нулевую гипотезу отвергают в пользу конкурирующей гипотезы; если наблюдаемое значение критерия принадлежит области принятия гипотезы, то нулевую гипотезу принимают.
5. Результат проверки гипотезы формулируется следующим образом: гипотеза 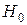 проверена по критерию
проверена по критерию 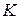 на уровне значимости
на уровне значимости 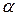 и принята (не противоречит имеющимся экспериментальным данным) или отвергнута.
и принята (не противоречит имеющимся экспериментальным данным) или отвергнута.
Пример.
Проверка гипотезы о равенстве средних двух нормально распределенных совокупностей с неизвестными, но равными дисперсиями по малым выборкам ( 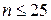 )
)
Пусть имеются две нормально распределенные генеральные совокупности 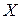 и
и 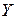 , характеризуемые генеральными средними
, характеризуемые генеральными средними 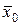 и
и 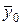 . Для проверки гипотезы из этих совокупностей берутся две независимые выборки объемов
. Для проверки гипотезы из этих совокупностей берутся две независимые выборки объемов 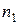 и
и 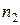 , по которым находят выборочные средние
, по которым находят выборочные средние 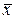 ,
, 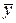 и исправленные выборочные дисперсии
и исправленные выборочные дисперсии 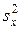 ,
, 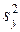 .
.
1. Нулевая гипотеза 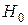 :
: 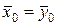 .
.
Альтернативная гипотеза 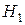 : а)
: а) 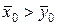 (
( 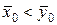 );
);
б) 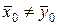 .
.
2. Уровень значимости 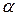 .
.
3. Статистический критерий: 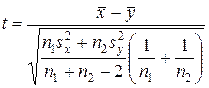 (22)
(22)
Критерий 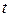 имеет распределение Стьюдента с
имеет распределение Стьюдента с 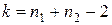 степенями свободы.
степенями свободы.
а) При альтернативной гипотезе 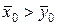 (
( 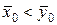 ) критическая область является односторонней и определяется неравенством
) критическая область является односторонней и определяется неравенством 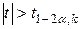 . Критическая точка определяется по таблице значений
. Критическая точка определяется по таблице значений 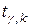 распределения Стьюдента, где
распределения Стьюдента, где 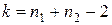 ,
, 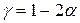 .
.
б) При альтернативной гипотезе 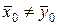 критическая область является двусторонней и определяется неравенством
критическая область является двусторонней и определяется неравенством 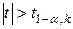 . Критическая точка определяется по таблице значений
. Критическая точка определяется по таблице значений 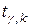 распределения Стьюдента, где
распределения Стьюдента, где 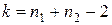 ,
, 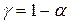 .
.
4. По формуле (22) определяем эмпирическое значение 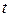 -критерия.
-критерия.
Гипотеза 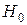 принимается, если: а)
принимается, если: а) 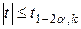 ;
;
б) 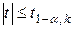 .
.
5. Делается вывод о результатах проверки гипотезы 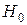 .
.
Основные понятия корреляционного и регрессионного анализов
При одновременном изучении нескольких признаков какого-либо объекта или учете нескольких показателей в эксперименте возникает вопрос о взаимосвязях между исследуемыми величинами. Наиболее разработанными в математической статистике методами анализа взаимосвязей являютсякорреляционный и регрессионный анализы.
При изучении взаимосвязи признаки делятся на два класса:
· признаки, обуславливающие изменения других признаков, называются факторными, или факторам;
· признаки, изменяющиеся под действием факторных признаков, называются результативными.
Связь называется статистической, если каждому значению факторного признака соответствует определенное (условное) распределение результативного признака. Корреляционной связью называется частный случай статистической связи, состоящий в том, что разным значениям факторного признака соответствуют различные средние значения результативного.
Корреляционная зависимость между признаками 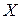 и
и 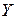 может быть представлена в виде уравнения:
может быть представлена в виде уравнения:
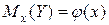 ,
,
где 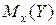 – условное математическое ожидание признака
– условное математическое ожидание признака 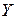 при заданном
при заданном 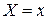 . Это уравнение называется теоретическим уравнением регрессии (или функцией регрессии)
. Это уравнение называется теоретическим уравнением регрессии (или функцией регрессии) 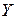 на
на 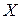 , а его график – теоретической линией регрессии.
, а его график – теоретической линией регрессии.
Парная регрессия
В зависимости от вида функции 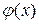 различают линейную и нелинейную регрессию.
различают линейную и нелинейную регрессию.
Для отыскания теоретического уравнения регрессии необходимо знать закон распределения двумерной случайной величины 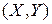 . Но на практике исследователь располагает выборкой пар значений
. Но на практике исследователь располагает выборкой пар значений 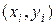 ограниченного объема
ограниченного объема 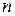 . В этом случае можно построить лишь наилучшую оценку для функции регрессии, которой является выборочное уравнение регрессии
. В этом случае можно построить лишь наилучшую оценку для функции регрессии, которой является выборочное уравнение регрессии 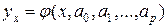
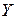 на
на 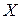 (или просто уравнение регрессии), где
(или просто уравнение регрессии), где 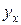 – условная средняя признака
– условная средняя признака 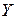 при фиксированном значении признака
при фиксированном значении признака 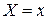 ,
, 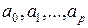 – параметры уравнения регрессии.
– параметры уравнения регрессии.
Так, например, оценкой линейного уравнения регрессии 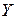 на
на 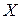 является выборочное уравнение регрессии
является выборочное уравнение регрессии 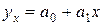 .
.
Параметры 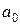 и
и 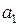 выборочного уравнения регрессии находятся следующим образом:
выборочного уравнения регрессии находятся следующим образом:
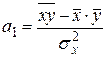 ; (23)
; (23)
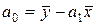 , (24)
, (24)
где 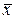 – выборочная средняя факторного признака
– выборочная средняя факторного признака 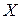 ,
, 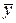 – выборочная средняя результативного признака
– выборочная средняя результативного признака 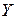 ,
, 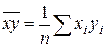 – средняя из произведений соответствующих значений факторного и результативного признаков,
– средняя из произведений соответствующих значений факторного и результативного признаков, 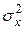 – выборочная дисперсия факторного признака
– выборочная дисперсия факторного признака 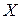 .
.
Коэффициент 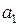 в уравнении регрессии называется коэффициентом регрессии (выборочным). Он показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.
в уравнении регрессии называется коэффициентом регрессии (выборочным). Он показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.
