Вопрос 14.1. Дифференциал функции нескольких переменных

N ‑ мерное арифметическое пространство 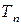мы рассматривали до сих пор как множество точек 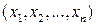. Между тем часто это пространство можно рассматривать как пространство векторов, понимая под вектором набор чисел 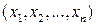. Действия над векторами определим следующим образом:

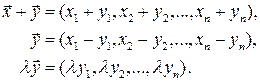
Теперь функцию 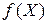можно обозначить 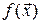, и считать, что она определена на множестве векторов, которые для удобства будем называть точками.

Определение 14.1. Полным приращением функции n переменных в точке 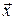называется следующая разность

.

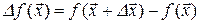Определение 14.2. Функция n переменных 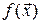называется дифференцируемой в точке 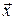, если ее полное приращение в этой точке можно представить следующим образом

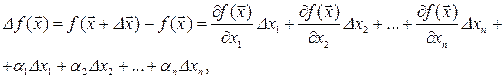
где 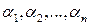‑ бесконечно малые функции при .

Пример 14.1. 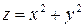, полное приращение этой функции имеет вид

,

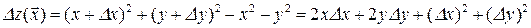т.е. функция дифференцируема в любой точке плоскости.

Конец примера.

Определение 14.3. Дифференциалом функции n переменных называется главная линейная часть полного приращения функции, то есть

.

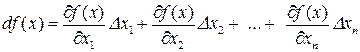Дифференциалы самих независимых переменных определим как их приращения, то есть

,

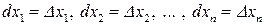тогда дифференциал функции принимает вид

.

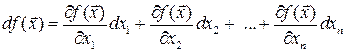Теорема 14.1. (необходимое условие дифференцируемости функции). Для дифференцируемости функции необходимо существование частных производных.

Доказательство очевидно.

Теорема 14.2. (достаточное условие дифференцируемости функции).

Для дифференцируемости функции достаточно непрерывности ее частных производных.

Доказательство. При доказательстве ограничимся функциями 2-х переменных. Рассмотрим полное приращение функции

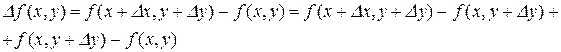
По теореме Лагранжа

.

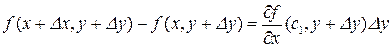Аналогично

,

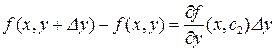отсюда

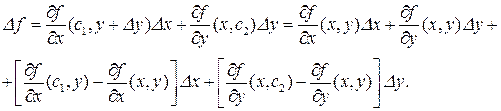
Выражения стоящие в квадратных скобках в силу непрерывности частных производных есть бесконечномалые функции при 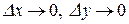, то есть функция по определению дифференцируема.

Конец доказательства.

Пример 14.2. 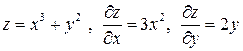‑ эти производные непрерывны, поэтому функция дифференцируема и .

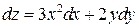Конец примера.

Используя определение дифференциала, несложно доказать следующие правила дифференцирования:

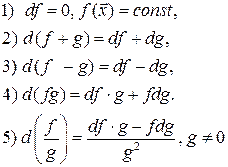
Вопрос 14.2. Дифференцирование сложной функции. Инвариантность формы первого дифференциала.

Теорема 14.3. Пусть функция 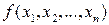дифференцируема в точке 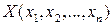, а функции

,

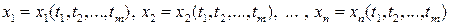дифференцируемы в точке 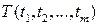. Тогда сложная функция 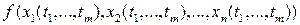дифференцируема в точке T и справедливы формулы:

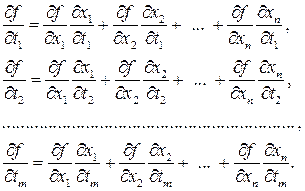
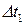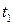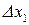Доказательство. При доказательстве ограничимся случаем функции двух переменных. Пусть приращение переменной , а и 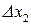‑ приращения функци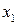й и 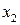- соответственно. Тогда

.

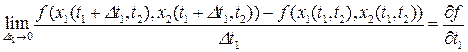Но 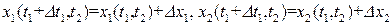, поэтому разность, стоящую в пределе для дифференцируемой функции можно записать в виде

,

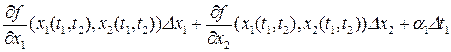где учтено, что

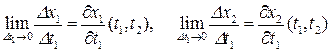
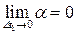, то есть 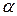- бесконечно малая величина.

Тогда подставляя все это в предел, получим

.

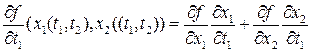Аналогично доказывается формула

.

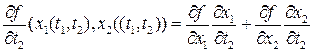Конец доказательства.

Пример 14.3. Вычислить произвоные:

.

.

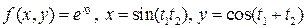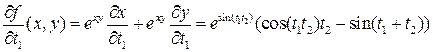Аналогично, найдем что

.

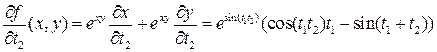Конец примера.

Теорема 14.4. (Инвариатность первого дифференциала). Форма первого дифференциала имеет один и тот же вид независимо от того, являются ли переменные независимыми или нет.

Доказательство. Ограничимся функциями двух переменных. Пусть 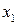и 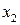зависимые переменные, то есть функции переменных 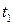и :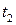

.

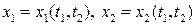Тогда

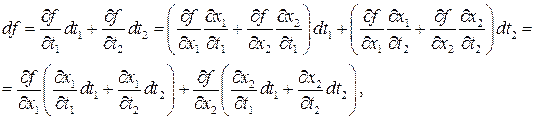
но

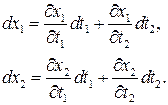
Отсюда

,

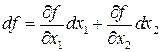то есть тот же вид первого дифференциала, как и в случае независимых переменных 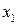и .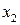

Конец доказательства.