Особенности процессов в линейных нестационарных системах

Линейная САУ называется нестационарной, если её параметры (коэффициенты, постоянные времени и т.п.) меняются во времени. Это обстоятельство приводит к изменению коэффициентов соответствующего дифференциального уравнения. Оно также служит признаком нестационарности системы.

Так как коэффициенты дифференциального уравнения стационарной САУ зависят от времени, то логично предположить, что от этого же времени будут зависеть все её свойства, в том числе: устойчивость, качество переходных процессов, характеристики установившегося состояния при любых типах входных воздействий.

В отличие от линейных стационарных систем, обладающих характеристическим уравнением с постоянными коэффициентами, линейные нестационарные САУ имеют характеристическое уравнение в виде нелинейного дифференциального уравнения.

Найти его корни и по ним оценить устойчивость нестационарной САУ практически невозможно даже в системе второго порядка.

Поэтому иногда пытаются судить о свойствах нестационарной САУ по корням так называемого формального характеристического уравнения, получаемого обычным формальным путем (заменой знака дифференцирования оператором p=d/dt) из соответствующего дифференциального уравнения.

Например, для дифференциального уравнения

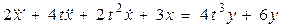(1)

формальное характеристическое уравнение имеет вид

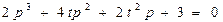. (2)

Уравнение (2) позволяет в первом приближении судить о свойствах нестационарной САУ, если его коэффициенты сравнительно медленно меняются во времени. Для этого используется метод “замороженных” коэффициентов.

Данный метод используется в двух вариантах:

· “замораживание” с постоянными параметрами;

· “замораживание” с переменными параметрами.

В первом варианте, чтобы получить постоянные параметры, поступают, следующим образом:

- берут дифференциальное уравнение вида (1);

- задаются некоторым временем 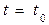, вблизи которого хотят узнать о свойствах САУ;

- вычисляют коэффициенты уравнения типа (1) при 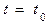, вследствие чего приходят к дифференциальному уравнению с постоянными коэффициентами.

Далее, по этому дифференциальному уравнению судят о всех свойствах нестационарной САУ вблизи точки 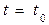.Эти суждения тем ближе к истине, чем медленнее меняются во времени коэффициенты уравнения (1).

Во втором варианте (“замораживание” с переменными параметрами) за характеристическое уравнение нестационарной САУ берут уравнение вида (2). Его корни будут уже функциями времени. Если они медленно меняются во времени, то информация о поведении САУ во времени более достоверна, чем при полном замораживании коэффициентов. Однако при сильном изменении параметров оба метода могут приводить к принципиальным ошибкам.

Таким образом, выявляется еще одна особенность нестационарных САУ: в них нельзяговорить об устойчивости в целом, а можно говорить лишь об устойчивости отдельных компонентвектора состояния или вектора выхода.