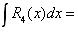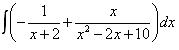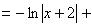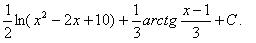Примеры выполнения типового расчета

Интегрирование рациональных дробей

Теоретическое введение

Рациональной дробью называется отношение двух многочленов:

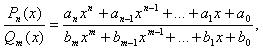
где a₀, a₁, ..., a_n, b₀, b₁, ..., b_n – действительные числа.
Рациональная дробь называется правильной, если степень числителя строго меньше степени знаменателя (n < m), в противном случае (n ≥ m) – дробь называется неправильной. Например, дробь
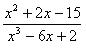– правильная, а дроби 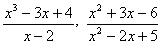– неправильные.
У любой неправильной дроби можно выделить ее целую часть, т.е. представить ее в виде суммы многочлена и правильной дроби.
Всякая правильная дробь может быть представлена в виде суммы конечного числа простейших дробей следующих четырех типов:
1) ;
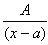2) 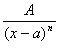(n > 1 – натуральное число);
3) ;
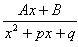4) 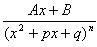(n > 1 – натуральное число, p² – 4q < 0, т.е. многочлен, стоящий в знаменателе не имеет действительных корней).

1.1.1 Схема интегрирования рациональных дробей
Для интегрирования рациональной дроби необходимо:
1) Если дробь неправильная – представить ее в виде суммы многочлена и правильной дроби.
2) Разложить правильную дробь на сумму простейших дробей.
3) Найти интеграл многочлена и всех простейших дробей.

1.1.2 Интегрирование простейших рациональных дробей
Простейшая дробь первого типа: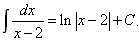
Простейшая дробь второго типа: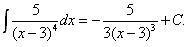
Простейшая дробь третьего типа: 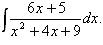Вычисление интеграла от нее заключается в интегрировании квадратного трехчлена в знаменателе.
1) Выделим полный квадрат суммы в знаменателе подынтегральной функции.

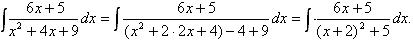
2) Выполним замену переменной, приняв выделенный двучлен х + 2 за новую переменную. Далее для удобства следующих преобразований выразим х через переменную t.

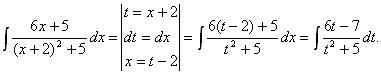
3) Выполним почленное деление числителя на знаменатель и представим полученный интеграл в виде разности двух интегралов.

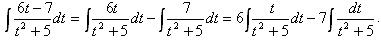
4) Первый интеграл вычислим с помощью метода замены переменной, взяв за новую переменную t знаменатель подынтегрального выражения, второй интеграл является табличным.


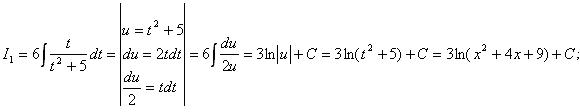
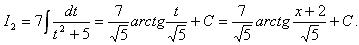
Таким образом,

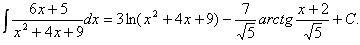
1.1.3 Выделение целой части у неправильной дроби
Любую неправильную дробь можно представить в виде суммы многочлена и остаточной правильной дроби. Для этого необходимо по правилу деления многочленов разделить числитель на знаменатель. Искомым многочленом является результат деления, числителем правильной дроби – остаток деления, знаменателем – делитель.
Пример.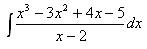
Решение
Так как степень числителя (3) выше степени знаменателя (1), то данная дробь является неправильной. Разделим числитель на знаменатель по правилу деления многочленов.

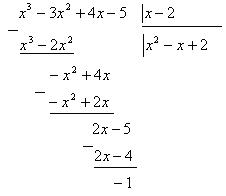
Таким образом,

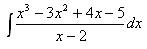
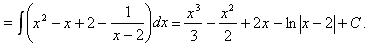
1.1.4 Разложение правильной дроби на сумму простейших дробей
Любой многочлен Q_m(x) с вещественными коэффициентами разлагается (и притом единственным способом с точностью до перестановки сомножителей) на произведение множителей первой степени вида (х – а) и множителей второй степени вида (x² + px + q). Разложение правильной дроби на сумму простейших дробей зависит от того, каким образом многочлен Q_m(x), стоящий в знаменателе, раскладывается на множители. Рассмотрим различные варианты разложения.
1) Знаменатель раскладывается лишь на неповторяющиеся множители первой степени вида (х – а).
В этом случае в разложении правильной дроби на сумму простейших каждому неповторяющемуся множителю первой степени соответствует слагаемое вида 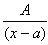, где А – неизвестный числовой коэффициент, который необходимо найти в дальнейшем ходе решения.
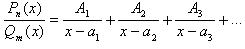(n < m )
2) Знаменатель раскладывается лишь на множители первой степени, среди которых есть повторяющиеся.
В этом случае в разложении правильной дроби на сумму простейших каждому повторяющемуся r раз множителю соответствуют слагаемые

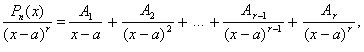
где A₁, A₂, ..., A_r-1, A_r – неизвестные числовые коэффициенты, которые необходимо найти в дальнейшем ходе решения.
3) Знаменатель раскладывается на множители второй степени вида (x² + px + q) и, возможно, множители первой степени.
Под множителем второй степени мы будем понимать многочлен вида (x² + px + q) без действительных корней, т.е. D = p² – 4q < 0. Каждому неповторяющемуся множителю второй степени в разложении правильной дроби на простейшие соответствует слагаемое 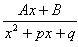, где А и В – неизвестные числовые коэффициенты.

Содержание типового расчета

Найти неопределенные интегралы для трех заданных рациональных дробей, разложив предварительно их на простейшие дроби.

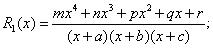
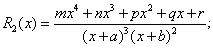
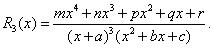
Примеры выполнения типового расчета

В качестве примеров решим задачи, не совпадающие с приведенными условиями типового расчета.
Пример 1. Найти неопределенный интеграл для рациональной дроби:

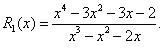
Решение
Так как степень числителя в подынтегральном выражении выше степени знаменателя, то эта рациональная дробь является неправильной. Поэтому на первом этапе решения необходимо выделить ее целую часть методом деления многочлена на многочлен.

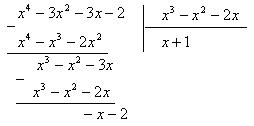
Следовательно,

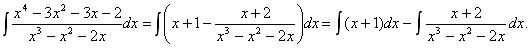
Интеграл от целой части (многочлена) вычисляется элементарно:

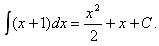
Вычислим теперь интеграл от правильной рациональной дроби. На первом шаге интегрирования необходимо разложить правильную дробь на сумму простейших дробей.
Вначале разложим знаменатель на множители. Если многочлен имеет действительные корни x₁ = a₁, x₂ = a₂, ..., x_k = a_k , то его можно разложить на множители (x₁ – a₁), (x₂ – a₂) , ... ,(x_k – a_k ). Поэтому найдем корни уравнения x³ – x² – 2x = 0.
Вынесем за скобки общий множитель x:
x³ – x² – 2x = x(x² – x – 2).
Отсюда следует, что первый корень многочлена, стоящего в знаменателе x₁ = 0.
Корнями квадратного уравнения x² – x – 2 = 0 являются x₂ = – 1 и x₃ = 2. Таким образом, x³ – x² – 2x = x(x² – x – 2) = x(x + 1)(x – 2). Все полученные множители имеют вид (x – a), т.е. являются множителями первой степени. Все множители разные. Поэтому имеет место следующее разложение:

,

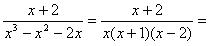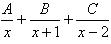(1)

где A, B, C – неизвестные числовые коэффициенты.
Приступаем к нахождению неизвестных числовых коэффициентов. Для этого приведем в правой части равенства (1) к общему знаменателю:

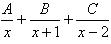
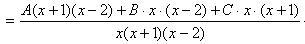
Таким образом, мы получили тождество:

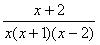
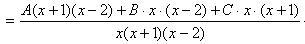
Две дроби тождественно равны между собой и имеют одинаковые знаменатели, следовательно, тождественно равны и их числители:

x + 2 = A(x + 1)(x – 2) + Bx(x – 2) + Cx(x + 1)

(2)

Для нахождения неизвестных коэффициентов A, B, C применим метод частных значений. Он заключается в том, что аргументу x придают некоторые удобные значения (таковыми являются значения корней многочлена). В результате получаем систему линейных уравнений относительно неизвестных числовых коэффициентов. Так, в рассматриваемом примере корни многочлена: x₁ = 0, x₂ = – 1, x₃ = 2. Подставим эти значения в равенство (2).

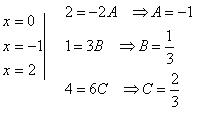
Тем самым коэффициенты найдены. Подставляем их в равенство (1)

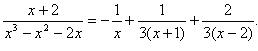
В результате интеграл от правильной рациональной дроби преобразовался в интеграл от суммы простейших дробей:

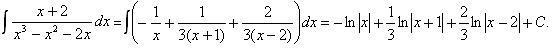
Таким образом, интеграл от заданной рациональной дроби равен

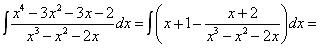
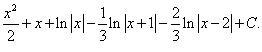
Пример 2. Найти неопределенный интеграл для рациональной дроби:
.
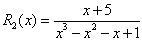Решение
В заданной функции степень числителя меньше степени знаменателя, поэтому рациональная дробь правильная. Разложим ее на сумму простейших дробей.
1) Разложим знаменатель на множители.
x³ – x² – x + 1 = x² (x – 1) – (x – 1) = (x – 1)(x² – 1) = (x – 1)(x – 1)(x + 1) = (x – 1)² (x + 1).
2) Разложим правильную дробь на сумму простейших дробей. В знаменателе есть два множителя первой степени (x + 1) и (x – 1)², причем множитель (x – 1) повторяется 2 раза. Множителю (x + 1) в разложении подынтегральной функции будет соответствовать простейшая дробь 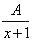, а множителю (x – 1)² будет соответствовать сумма двух простейших дробей 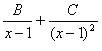. Поэтому имеет место следующее разложение:
+ .
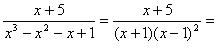
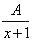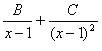3) Найдем неизвестные коэффициенты A, B и C. Приведем в правой части равенства к общему знаменателю и приравняем числители двух тождественно равных дробей.
+ .

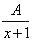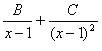
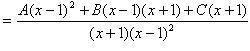x + 5 = A(x – 1)2 + B(x – 1)(x + 1) + C(x + 1)

(3)

Воспользуемся методом частных значений. Подставим в левую и правую часть равенства значения корней многочлена, стоящего в знаменателе.

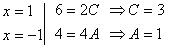
Однако, корней многочлена больше нет, а значение коэффициента В еще не найдено. В этом случае применяют метод неопределенных коэффициентов. Основная идея метода состоит в том, что если два многочлена тождественно равны между собой, то равны числовые коэффициенты, стоящие при одинаковых степенях х.
Чтобы применить метод неопределенных коэффициентов, раскроем скобки в правой части равенства (3):
x + 5 = A(x – 1)² + B(x – 1)(x + 1) + C(x + 1) = A(x² – 2x + 1) + B(x² – 1) + C(x + 1).
Приравнивая коэффициенты при одинаковых степенях х, начиная со старшей, получим систему трех уравнений с тремя неизвестными, откуда найдем неизвестные коэффициенты.

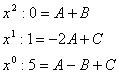
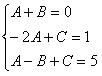
Однако, два коэффициента А и С уже найдены методом частных значений. Значит, чтобы найти коэффициент В, нам необходимо только первое уравнение:
A + В = 0;
1 + В = 0 => В = – 1.

Подставим найденные коэффициенты:

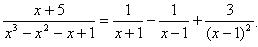
4) Заменим под знаком интеграла правильную рациональную дробь ее разложением на сумму простейших дробей, представим новый интеграл в виде суммы интегралов и найдем их.


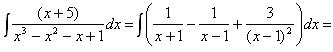
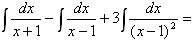
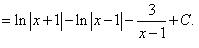
Пример 3. Найти неопределенный интеграл .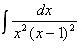
Решение
Подынтегральная функция – правильная рациональная дробь. Знаменатель уже представлен в виде двух множителей первой степени, каждый из которых повторяется 2 раза. Значит, разложение на сумму простейших дробей выглядит следующим образом:

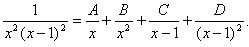
Найдем неизвестные коэффициенты. Для этого приведем дроби в правой части к общему знаменателю и приравняем числители:

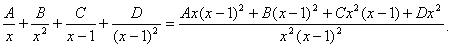
1 = Аx(x – 1)² + B(x – 1)² + Cx²(x – 1) + Dx².
Воспользуемся методом частных значений, подставив вместо х значения корней многочлена:

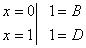
Так как корней больше нет, применим метод сравнения коэффициентов. Для этого раскроем скобки в правой части равенства числителей:
1 = Аx(x – 1)² + B(x – 1)² + Cx²(x – 1) + Dx² = А(x³ – 2x² + x) + B(x² – 2x + 1) + C(x³ – x²) + Dx².
Нам необходимо найти два коэффициента, поэтому достаточно получить систему из двух уравнений.
x³ : 0 = А + C;
x² : 0 = – 2А + B – C + D.
Подставив, найденные ранее значения B и D, получили систему:

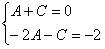
Сложим два уравнения и найдем коэффициент А:
– А = – 2 => А = 2.
Из первого уравнения С = – 2.
Получили следующее разложение в виде суммы простейших дробей:

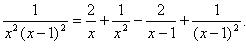
Выполним интегрирование:

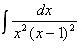
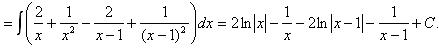
Пример 4. Найти неопределенный интеграл .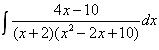
Решение
Под знаком интеграла находится правильная рациональная дробь. Квадратный трехчлен x² – 2x + 10 не имеет действительных корней, т.к. D = 4 – 40 < 0, следовательно, он является множителем второй степени.
Таким образом, знаменатель в подынтегральном выражении раскладывается на неповторяющийся множитель первой степени (x + 2) и неповторяющийся множитель второй степени (x² – 2x + 10). Поэтому разложение рациональной дроби на сумму простейших дробей имеет следующий вид:
.
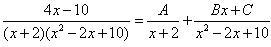Отсюда,
4x – 10 = A(x² – 2x + 10) + (Bx + C)(x + 2) = 4x – 10 = A(x² – 2x + 10) + Bx² + Cx + 2Bx + 2C.
Присвоим аргументу х значение корня многочлена x = – 2:
x = – 2| – 18 = 18A => A = – 1.
Приравняем коэффициенты при одинаковых степенях х:
x² : 0 = A + B;
x¹ : 4 = – 2A + C + 2B.
Получили систему линейных уравнений:

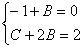
Из первого уравнения В = 1, подставив это значение во второе уравнение, найдем C = 0.
Следовательно,
.
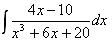
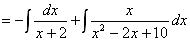Первый из полученных интегралов равен

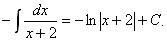
Для вычисления второго интеграла воспользуемся алгоритмом интегрирования квадратного трехчлена в знаменателе.



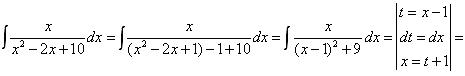
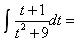
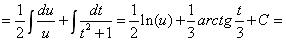
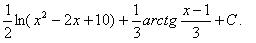
В итоге получили:

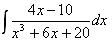
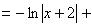
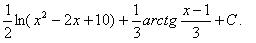
Оформление отчета

В отчете должно быть представлено разложение каждой правильной дроби на простейшие, интегрирование полученных простейших дробей. В ответе необходимо записать каждую дробь в виде суммы целой части, если она есть, и простейших дробей, а затем требуемый интеграл. Ниже приведены образцы ответов рассмотренных выше примеров.
1.
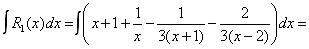
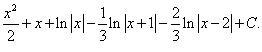
2.
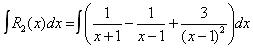
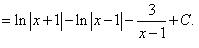
3.
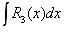
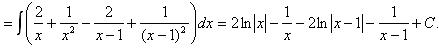
4.