Аппроксимация функций: метод наименьших квадратов
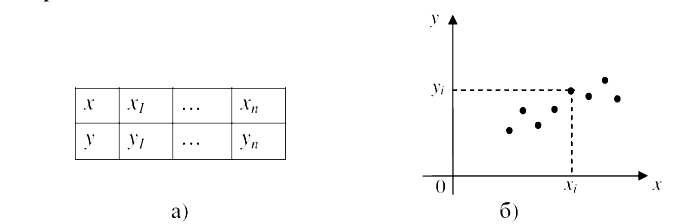
При экспериментальном изучении зависимостей у от х производят ряд измерений величины у при разных значениях величины х. Результат измерений представляют таблицей (рис.а) или точечной диаграммой (рис.б)
Значения функции 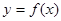 при
при 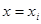 определены приближенно с некоторой случайной погрешностью. Наличие этой погрешности делает нецелесообразным подбор такой приближенной функции, которая точно бы проходила через все экспериментальные данные, т.е. через точку
определены приближенно с некоторой случайной погрешностью. Наличие этой погрешности делает нецелесообразным подбор такой приближенной функции, которая точно бы проходила через все экспериментальные данные, т.е. через точку 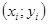 ,
, 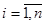 . Лучше подобрать такую аппроксимацию, которая бы сглаживала случайные погрешности измерений.
. Лучше подобрать такую аппроксимацию, которая бы сглаживала случайные погрешности измерений.
Для приближения (аппроксимации) неизвестной теоретической функции 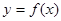 будем использовать обобщенный многочлен
будем использовать обобщенный многочлен 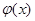 , при этом
, при этом 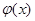 называют эмпирической функцией, а ее график – эмпирической кривой.
называют эмпирической функцией, а ее график – эмпирической кривой.
Задача нахождения (построения) 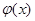 состоит из двух этапов:
состоит из двух этапов:
1) Определение вида аппроксимирующей функции 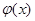 .
.
2) Определение параметров (коэффициентов 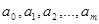 ) функции
) функции 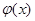 .
.
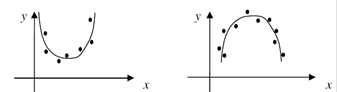
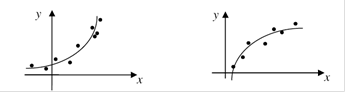
1 этап: При определении вида аппроксимирующей функции 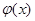 исходят из характера расположения экспериментальных точек.
исходят из характера расположения экспериментальных точек.
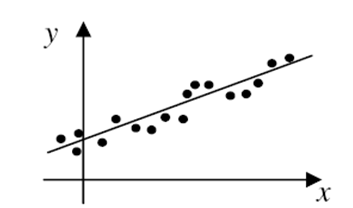
Так, если точки располагаются вдоль некоторой прямой, то в качестве 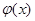 выбирают
выбирают 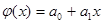 - симметричную функцию, зависящую от двух параметров
- симметричную функцию, зависящую от двух параметров 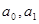 .
.
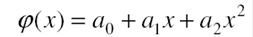
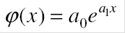
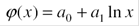
2 этап: Определение параметров аппроксимирующей функции по методу наименьших квадратов (МНК).
Пусть определен вид аппроксимирующей функции 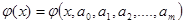 . Подбор параметров будем осуществлять таким образом, чтобы сумма квадратов отклонений ординат аппроксимирующей функции от экспериментальных значений
. Подбор параметров будем осуществлять таким образом, чтобы сумма квадратов отклонений ординат аппроксимирующей функции от экспериментальных значений 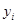 ,
, 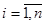 была наименьшей.
была наименьшей.
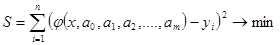
Рассмотрим применение метода на примере.
изучают статистическую совокупность людей одновременно по обхвату груди 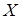 и росту
и росту 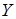 .
.
Пусть в результате изучения получены данные:
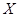 | 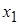 | 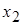 | … | 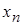 |
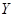 | 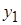 | 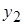 | … | 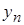 |
Эта таблица выражает некоторую функциональную зависимость между 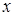 и
и  , и задача состоит в том, чтобы по этой таблице установить какую именно целесообразно принять аналитическую формулу связи между
, и задача состоит в том, чтобы по этой таблице установить какую именно целесообразно принять аналитическую формулу связи между 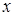 и
и  . Для решения этого вопроса, рассматривая упорядоченные пары чисел
. Для решения этого вопроса, рассматривая упорядоченные пары чисел 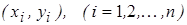 данной таблицы как точки на координатной плоскости, построим их. Может оказаться, что точки группируются около некоторой прямой, т.е. можно приближенно считать зависимость между переменными
данной таблицы как точки на координатной плоскости, построим их. Может оказаться, что точки группируются около некоторой прямой, т.е. можно приближенно считать зависимость между переменными 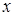 и
и  линейной
линейной
 , (1)
, (1)
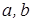 – коэффициенты которые находятся по методу наименьших квадратов при решении системы
– коэффициенты которые находятся по методу наименьших квадратов при решении системы
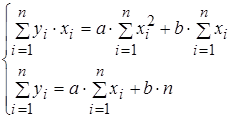 (2)
(2)
Пример 1.
Пусть из опыта получена таблица
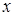 | -2 | ||||
 | 0,5 | 1,5 |
Методом наименьших квадратов найти эмпирическую формулу функциональной зависимости между 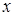 и
и  .
.
Построим на плоскости  точки
точки 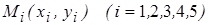 .
.
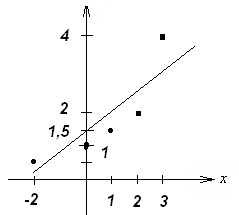
Видно, что построенные точки группируются около некоторой прямой  . Коэффициенты
. Коэффициенты 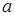 и
и 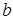 находим при решении системы (2).
находим при решении системы (2).
| № | 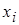 | 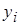 | 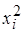 | 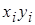 | 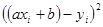 |
| -2 | 0,5 | -1 | 0,03 | ||
| 0,03 | |||||
| 1,5 | 1,5 | 0,01 | |||
| 0,0006 | |||||
| 0,016 | |||||
| Сумма | 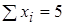 | 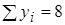 | 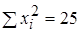 | 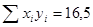 | 0,0866 |
Рис. 7.
Для вычисления коэффициентов 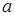 и
и 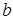 составим таблицу:
составим таблицу:
Подставим найденные суммы в систему (2):
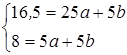
Вычитая из первого уравнения второе, получим:
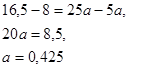 .
.
Подставляя значение 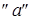 во второе уравнение, получим
во второе уравнение, получим
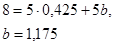 .
.
Найденные значения 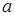 и
и 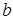 подставим в уравнение (1):
подставим в уравнение (1):
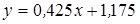 .
.
Ошибка аппроксимации составляет 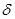 = 0,0866.
= 0,0866.
Пример 2.
В табл. приведены аргументы 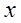 и значения
и значения 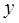 некоторой функции.
некоторой функции.
Требуется:
1) методом наименьших квадратов найти наилучшие значения параметров 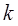 и
и 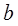 в уравнении прямой
в уравнении прямой 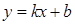 , аппроксимирующей заданную функцию;
, аппроксимирующей заданную функцию;
2) для заданной функции построить интерполяционный многочлен Лагранжа;
3) на одной координатной плоскости построить точки 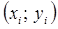 и полученные в пунктах 1 и 2 линии.
и полученные в пунктах 1 и 2 линии.
| х | ||||
| у |
Решение:
Заполним расчетную таблицу (пока, кроме ее последних трех столбцов).
В последней строке записываем суммы столбцов.
| № | x | y | 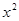 | xy |  |  - y - y | (  - y)2 - y)2 |
| сумма | |||||||
Для нахождения параметров функции 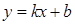 , составим нормальную систему уравнений
, составим нормальную систему уравнений
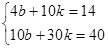 .
.
Решение этой системы дает следующие значения:
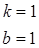
Ошибка аппроксимации составляет 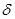 = 0.
= 0.
Т.о. искомое уравнение прямой имеет вид: 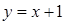 .
.
Построим график полученной прямой и заданные точки в ДСК.
