Метод эквивалентного генератора
Баланс мощностей
При составлении баланса мощностей будем использовать реальные направления токов, а не те, которые мы сами выбрали вначале. Алгебраическая сумма мощностей источников энергии должна быть равна сумме мощностей в сопротивлениях:
Ʃ Pист=Ʃ I2R, Pист=Uист*Iист.
Ʃ Pист=+i1E1 + i2E2+i3E3+i4E4+i5E5-iJUJ= +0.54*2+8.04*50+6.89*40+8.58*30+2.31*20-
-4*8.45=948.64[Вт]
Ʃ I2R= +i12*R1+i22 *R2+i32 *R3+i42 *R4+i52 *R5+i72 *R7+i82 *R8= +(0.54)2*6+(8.04)2*4+(6.89)2*5+(8.58)2*4+(2.31)2*5+(6.35)2*3+(1.69)2*3=948.64[Вт]
Задание №4
Определение показаний вольтметров.

Схема 4. Схема для определения показаний вольтметров.
V1=|ϕ1-ϕ2| ; ϕ1=ϕ2+I3R3-E3+I6R6-E6
V1=ϕ2+I3R3-E3+I6R6-E6-ϕ2=6.89*5-40+0-50=55.55[B]
V2=|ϕ3-ϕ4|; ϕ3=ϕ4-I4R4-E2+I2R2
V2=ϕ4-I4R4-E2+I2R2-ϕ4=-8.57*4-30+8.04*4=32.12[B]
Задание №5
Метод эквивалентного генератора.
Отключим вторую ветвь , а всю остальную часть цепи назовем активным двухполюсником.
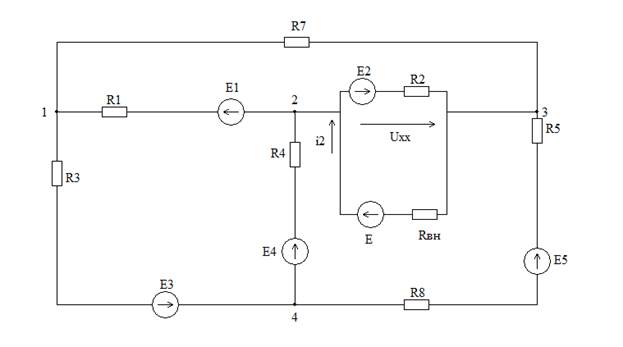
Схема 5. Метод эквивалентного генератора.
Чтобы определить ЭДС эквивалентного генератора, необходимо найти напряжение холостого хода активного двухполюсника. Точки 2 и 3 будем считать узлами. Методом узловых потенциалов найдем разность потенциалов узлов 2 и 3( ветвь 2 отключена).
G11ϕ11+G12ϕ22+G13ϕ33+G14ϕ44=I11
G21ϕ11+G22ϕ22+G23ϕ33+G24ϕ44=I22
G31ϕ11+G32ϕ22+G33ϕ33+G34ϕ44=I33
G41ϕ11+G42ϕ22+G43ϕ33+G44ϕ44=I44
Рассчитаем значения проводимостей и токов:
G11=1/R1+1/R3+1/R7=1/6+1/5+1/3=0.7[См]
G22=1/R1+1/R4=1/6+1/4=0.42[См]
G33=1/R5+1/R7=1/5+1/3=0.53[См]
G44=1/R3+1/R4+1/R8=1/5+1/4+1/3=0.78[См]
G12=G21=-1/R1=-1.6=-0.16[См]
G13=G31=-1/R7=-1/3=-0.33[См]
G14=G41=-1/R3=-1/5=-0.2[См]
G23=G32= =0 [См]
G24=G42=-1/R4=-1/4=-0.25[См]
G34=G43= =0[Cм]
I11=E1/R1-E3/R3=2/6-40/5=-7.66[A]
I22=-E1/R1+E4/R4=-2/6+30/4=7.17[A]
I33=E5/R5-I=20/5-4=0[A]
I44=E3/R3-E4/R4=40/5-30/4=0.5[A]
Подставим полученные значения в исходные уравнения.
0,7ϕ11-0,17ϕ22-0,33ϕ33-0,2ϕ44=-7,66
-0,17ϕ11+0,42ϕ22-0ϕ33-0,25ϕ44=7,17
-0,33ϕ11-0ϕ22+0,53ϕ33-0ϕ44=0
-0,2ϕ11-0,25ϕ22-0ϕ33+0,78ϕ44=0,5
Решая данную систему, получим:
ϕ11=-8,93[B], ϕ22=15.64[B],ϕ33=-5.58[B],ϕ44=3.35[B],
UXX=ϕ22-ϕ33=15.64-(-5.58)=21.22[B].
Для определения входного сопротивления двухполюсника отключим все источники в схеме. Перерисуем оставшиеся сопротивления.
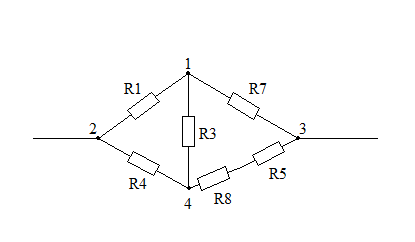
Преобразуем треугольник сопротивлений в эквивалентную звезду сопротивлений
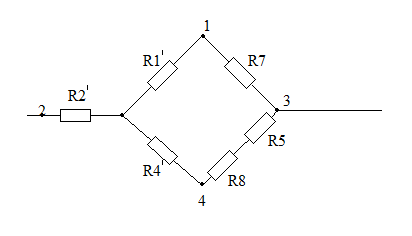
R2,=R1*R4/R1+R4+R3=6*4/6+4+5=1.6[Ом]
R1,=R1*R3/R1+R4+R3=6*5/6+4+5=2[Ом]
R4,=R4*R3/R1+R4+R3=4*5/6+4+5=1.33[Ом]
Rвн=R2,+(R1,+R7)(R4,+R8+R5)/R1,+R7+R4,+R8+R5=1.6+(2+3)(1.33+3+5)/2+3+1.33+3+5=4.86[Ом]
i2=UXX+E2/Rвн+R2=21.22+50/4.86+4=8.04[A]
Найдем значение дополнительной ЭДС
i,2=-2i2
i,2=UXX+E2-Eдоп/Rвн+R2=-2i2
Eдоп=UXX+E2+2i2(Rвн+R2)=21.22+50+2*8.04*(4.86+4)=213.66[B]
Задание 6
