Тема 1.1 Действия с числами

Самостоятельная работа №1.

Раздел 1. Введение.

Тема 1.1 Действия с числами.

Самостоятельная работа №1.(2 часа)

· повторить вычисления НОК и НОД;

· правила сложения, вычитания обыкновенных дробей;

· правила действий с десятичными дробями.

Чтобы сократить записи придумали обозначения НОД и НОК,что означает наибольший общий делитель и наименьшее общее кратное

Каждое число является делителем других чисел, которые называются кратными этому числу. К(22) = {22;44;66;88;110;…}

Изобразим множества делителей чисел 18, 24

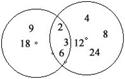Д(18) 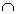Д(24)={2; 3; 6} ;Наибольший из общих делителей – 6, НОД(18; 24)=6

Изобразим множества кратных числам 18 и 24

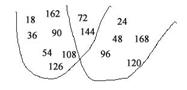К(18) 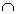К(24)={72; 144; …} – общие кратные 18 и 24

Наименьшее из общих кратных – 72. НОК(18; 24)= 72

Как находить НОД и НОК?

Для чисел 18 и 24 это просто:

- чтобы найти НОД перебираем общие делители 2; 3, пока не находим наибольший -6.

- чтобы найти НОК умножаем 18 на 2, на 3 и так далее, пока не найдем число, которое делится на 24 – это 72

Если же числа большие, то их раскладывают на простые множители

600 = 2³ ·3 ·5²

108 = 2² ·3²

НОД должен содержать все общие множители в наименьшей степени (подчеркнуты):

НОД (600; 108)= 2² ·3 = 12

НОК должен содержать все множители в наибольшей степени (жирный шрифт):

НОК(600;108) == 2³ ·3³ ·5² = 5400

НОД (27;14)=1, так как у них нет общих делителей, кроме 1. 27=3³, а 14 = 2·7

Такие числа называют взаимно простыми.

НОК(27;14)= 27·14 по той же самой причине, у них нет общих делителей.

Удобно использовать методы нахождения НОК при сложении дробей.

Наименьший общий знаменатель – это и есть НОК знаменателей..

НОД(408;90) 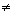1 НОК (408; 90) =2040

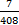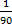12 - 56 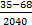= - 44 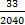+ = - 44 - = -44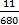

НОД (92; 51)=1– взаимно простые НОК(92;51)=92·51= 4692

При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляют тот же.
С помощью букв правило сложения можно записать так:

+ =

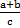
Буханку хлеба разрезали на 8 равных частей (долей). На тарелку положили 7 долей, а потом 4 доли съели. Осталось 3 доли, то есть

буханки:

- =

При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же.
С помощью букв правило вычитания можно записать так:

- =

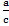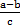
Ключевые слова: дробь, числитель, знаменатель, смешанное число, приведение к общему знаменателю, сложение, вычитание, умножение и деление дробей, правильная и неправильная дробь

Определение: Выражение вида 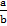или a : b, где а и b целые числа, b≠0, называется дробью

Число a называется числителем дроби. Число b называется знаменателем дроби

Если a < b, то выражение 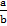правильная дробь

Если a > b , то выражение 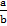неправильная дробь. Из любой неправильной дроби можно выделить целую часть и дробную часть. Примеры : = 2

Основное свойство дроби: Две дроб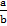и и 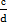называются равными если a·d=b·c.

Действия над дробям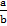и ( и ):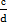

Дробь не изменится, если числитель и знаменатель дроби умножить на одно и то же число..

Если знаменатели разные, то дроби нужно привести к общему знаменателю. Для этого

· Каждый знаменатель разложить на множители

· Выписать множители первого знаменателя

· Добавить недостающие множители других знаменателей.

Общим знаменателем будет НОК (b, d)