Отказы, когда нагрузка превышает прочность детали
Проследить воздействие механической нагрузки на отказ в сложных современных машинах не представляется возможным, особенно если это касается оборудования, где отказы наблюдаются и в стационарных условиях. Мы не можем, например, в данный момент времени точно сказать, какая доля отказов в машине связана с наличием трещин в материале, раковин в спайке и сварке материалов. Эти дефекты в определенной мере влияют на долговечность и надежность. Изучение их даже независимо от других факторов, влияющих на надежность, помогает проектировщикам выбрать наиболее эффективные пути ее повышения.
Даже тщательно изготовленные образцы элементов конструкций значительно отличаются по своим прочностным качествам, не говоря уже о сложных конструкциях и реальных технологиях. При расчетах надежности необходимо учитывать статистический характер свойств реальных объектов.
Разброс прочностных параметров инженерных конструкций обычно вызывается большим количеством случайных факторов:
- неоднородностью материала,
- нестабильностью технологии изготовления,
- нестабильность условий эксплуатации и т. д.
Поэтому можно считать, что распределение предела прочности конструкций достаточно хорошо описывается нормальным законом. Реальные конструкции под действием достаточно интенсивного и частого потока воздействий приходят в колебательное движение.
Воздействия на конструкцию часто носят характер случайного непрерывного процесса, вызывающие соответственно непрерывные деформации изделий. В этом случае для анализа надежности используется теория случайных выбросов.
Назначается некоторый допустимый уровень для изменения параметров конструкции во времени (например, напряжения или деформации), фиксируется момент времени, когда выбранные параметры достигают этого критического уровня и считают его за момент отказа. Надежность конструкции, как вероятность нахождения выбранных параметров в допустимых интервалах, выражается хорошо знакомой нам формулой 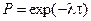 , где
, где 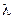 – интенсивность потока случайных выбросов.
– интенсивность потока случайных выбросов.
В случае нормального одномерного стационарного процесса
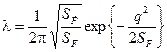 ,
,
где 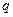 – допустимое значение для абсолютного значения случайной функции
– допустимое значение для абсолютного значения случайной функции 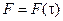 ;
; 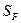 – среднеквадратичное отклонение этого процесса;
– среднеквадратичное отклонение этого процесса; 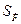 – среднеквадратичное отклонение производной случайного процесса, т. е. функции
– среднеквадратичное отклонение производной случайного процесса, т. е. функции 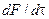 .
.
