Перечислите и поясните основные свойства простейшего потока отказов Пуассона

Приведите выражения для определения функции надежности, интенсивности частоты отказов элемента на основе статистических испытаний партии, состоящей из однородных элементов.

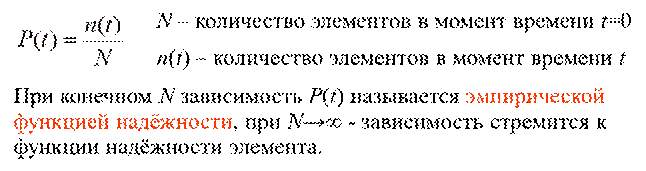
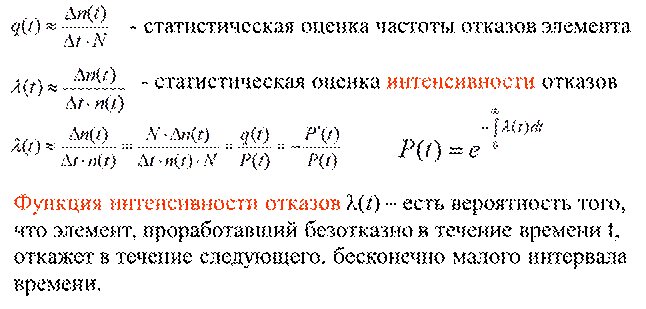
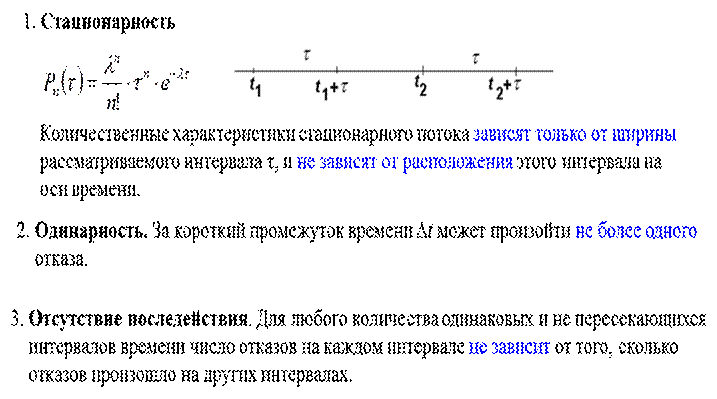
Перечислите и поясните основные свойства простейшего потока отказов Пуассона.

№3 Приведите зависимость интенсивности отказов элемента от времени и поясните особенности различных этапов его эксплуатации.

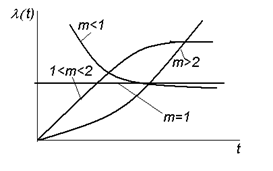
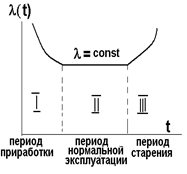
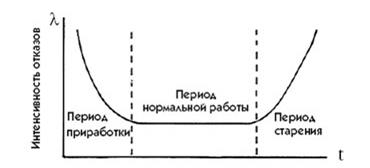Рис.1 - Зависимость изменения интенсивности отказов от времени

В первый отрезок времени, называемый периодом приработки, выходят из строя элементы, имеющие грубые дефекты, не вскрытые контролем.

После выявления этих элементов интенсивность отказов уменьшается и далее остаётся постоянной, наступает период нормальной работы.

По мере износа элементов интенсивность отказов вновь возрастает, начинается период старения элементов.

Значение периода приработки при эксплуатации следует учитывать в обязательном порядке. Именно в этот отрезок времени проявляются недостатки выходного контроля качества на предприятии изготовителе, а также ошибки, допущенные при транспортировке техники. Типовое значение этого периода составляет 2-3 недели с момента ввода изделия в эксплуатацию. Отказы в период приработки подчиняются закону Вейбулла (m < 1): .

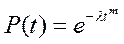Учет периода приработки – как аппроксимация функции надежности в этот период:

, ,

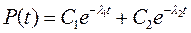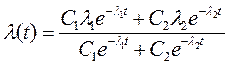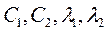- из услови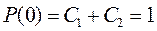й и .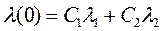

В период нормальной эксплуатации могут происходить внезапные отказы, которые имеют случайный характер (механические повреждения, повреждения вследствие неблагоприятных внешних условий и т.д.). Природа таких отказов обусловлена неожиданной концентрацией нагрузок внутри изделия (или извне). Закон распределения отказов в этот период экспоненциальный:

.

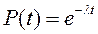Период старения и износа характеризуется резким увеличением интенсивности отказов и связан с интенсивным износом и старением, необратимыми физико-химическими процессами в материалах, из которых изготовлены элементы и их части (постепенные отказы). Закон распределения отказов — либо нормальный (логарифмически-нормальный) ,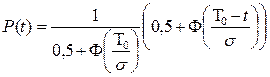

либо закон Вейбулла (m > 2), (могут быть и другие случаи).

4.При каком характере интенсивности отказов справедлив экспоненциальный закон надежности? Определите математическое ожидание и дисперсию времени безотказной эксплуатации элемент при этом законе надежности.

Экспоненциальный закон надёжности

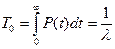
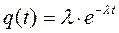
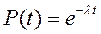
Для широкого класса элементов можно принять λ(t)=const

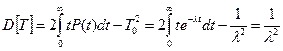
Важным свойством экспоненциального закона надёжности является то, что вероятность отказа элемента на интервале времени (t,t+Δt) не зависит от времени предшествующей работы t, а только от ширины интервала Δt.

Экспоненциальному закону подчиняются только отказы, носящие случайный характер. Отказы, связанные с приработкой или старением элемента этому закону уже не подчиняются.

5) Надёжность восстанавливаемого элемента

Под восстановлением элемента понимают либо замену вышедшего из строя элемента новым, либо такой ремонт, при котором исходные свойства объекта полностью восстанавливаются.

Предполагается что время восстановления пренебрежимо мало, по сравнению с временем эксплуатации элемента (восстановление происходит мгновенно).