Векторы. Основные определения.
Вектором называется направленный отрезок. К векторам относится также нулевой вектор, начало и конец которого совпадают. Вектор характеризуется своей длиной (модулем) и направлением.
B
A
Линейные операции над векторами:
1). Сложение векторов.
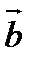
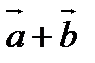
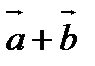
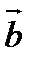
Складывают два вектора по правилу параллелограмма или треугольника. Правило треугольника можно обобщить на n-слагаемых. Если каждый раз соединять начало последующего вектора с концом предыдущего, то получим ломаную линию. Вектор, соединяющий начало первого с концом последнего и есть сумма.
2). Умножение вектора на число.
При умножении вектора 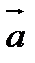 на число
на число 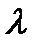 его модуль увеличивается (если
его модуль увеличивается (если 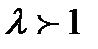 ) или уменьшается (если
) или уменьшается (если 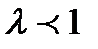 ) в
) в 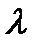 раз, а направление не изменяется, если
раз, а направление не изменяется, если 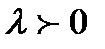 и меняется на противоположное, если
и меняется на противоположное, если 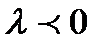 .
.
В любом случае векторы 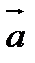 и
и 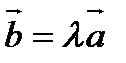 лежат на одной прямой или на параллельных прямых. Такие векторы называются коллинеарные.
лежат на одной прямой или на параллельных прямых. Такие векторы называются коллинеарные.
Нулевой вектор считается коллинеарным любому вектору.
Векторы, лежащие в одной плоскости или в параллельных плоскостях, называются компланарными.
Свойства линейных операций:
1). Коммутативность
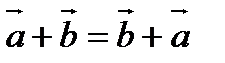
2). Ассоциативность
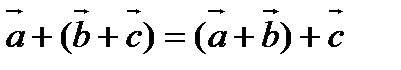 ,
, 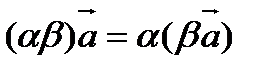
3). Дистрибутивность
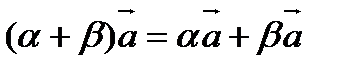
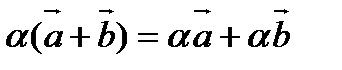 , где
, где 
Рассмотрим систему векторов 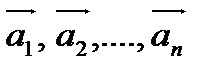 . Выражение вида
. Выражение вида 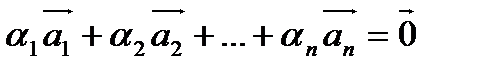 , где
, где 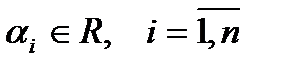 называется линейной комбинацией векторов
называется линейной комбинацией векторов 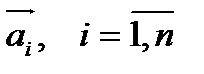 . Если в линейной комбинации все
. Если в линейной комбинации все 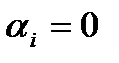 , то система векторов линейно независима. Если существуют
, то система векторов линейно независима. Если существуют 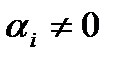 , то система – линейно зависима.
, то система – линейно зависима.
Любая упорядоченная линейно независимая тройка векторов 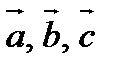 называется базисом в пространстве. Векторы
называется базисом в пространстве. Векторы 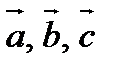 называются базисными. Если базисные вектора взаимно перпендикулярны, то базис называется ортогональным. Если базисные векторы имеют единичную длину, то они называются ортами. Базис называется ортонормированным, если базисные векторы единичные и взаимно перпендикулярные. Декартова система координат – ортонормированная, орты прямоугольной декартовой системы координат обозначают
называются базисными. Если базисные вектора взаимно перпендикулярны, то базис называется ортогональным. Если базисные векторы имеют единичную длину, то они называются ортами. Базис называется ортонормированным, если базисные векторы единичные и взаимно перпендикулярные. Декартова система координат – ортонормированная, орты прямоугольной декартовой системы координат обозначают 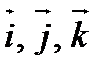 .
.
Пусть 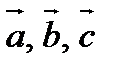 - некоторый базис в пространстве. Пусть
- некоторый базис в пространстве. Пусть 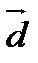 - произвольный вектор пространства. Рассмотрим линейную комбинацию
- произвольный вектор пространства. Рассмотрим линейную комбинацию
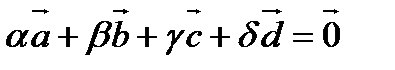
Так как любая четвёрка векторов линейно зависима, то не все коэффициенты линейной комбинации равны 0.
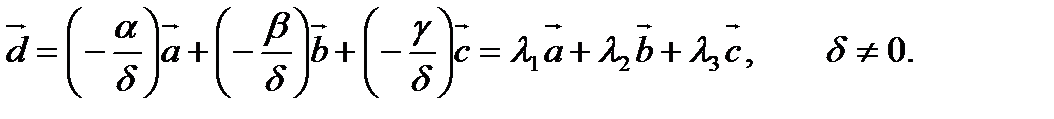
Эта формула даёт разложение вектора 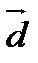 по базису (
по базису ( 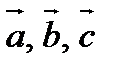 ). Коэффициенты
). Коэффициенты 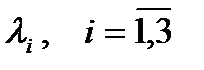 - координаты вектора
- координаты вектора 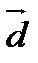 в этом базисе. Разложение вектора по базису единственное, т.е. координаты вектора однозначно определяют сам вектор.
в этом базисе. Разложение вектора по базису единственное, т.е. координаты вектора однозначно определяют сам вектор.
В связи с этим можно записать следующие свойства:
Пусть даны векторы 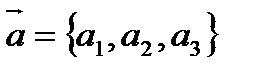 и
и 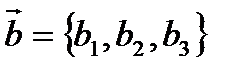
1). Равные векторы имеют одинаковые координаты, т.е. если 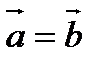 , то
, то 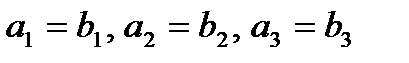 .
.
2). При умножении вектора на число, его координаты умножаются на это число 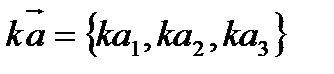 .
.
3). При сложении двух векторов складываются их соответствующие координаты 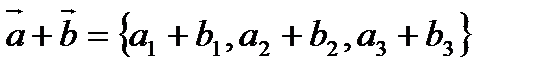 .
.
Проекцией вектора 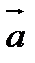 на вектор
на вектор 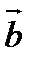 называется число
называется число 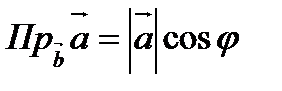 , где
, где 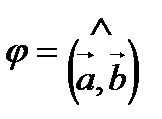 .
.
Координаты вектора 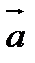 в прямоугольном базисе совпадают с проекциями вектора
в прямоугольном базисе совпадают с проекциями вектора 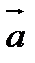 на базисные орты
на базисные орты 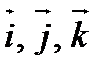 , а длина вектора равна
, а длина вектора равна
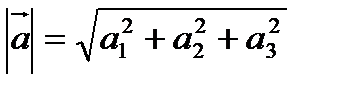
Числа 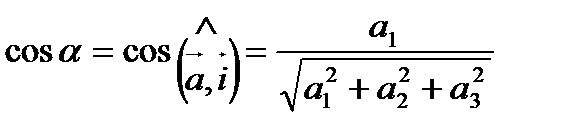
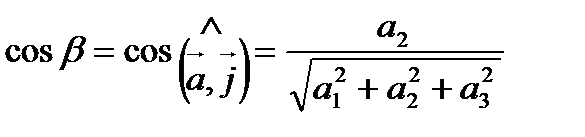
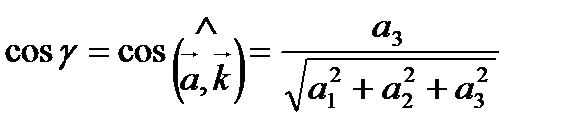
называются направляющими косинусами вектора 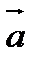 .
.
Скалярное произведение.
Скалярным произведением двух векторов 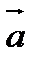 и
и 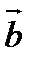 называют число равное
называют число равное 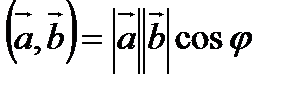 , где
, где 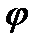 - угол между векторами
- угол между векторами 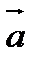 и
и 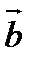 .
.
Свойства скалярного произведения:
1). 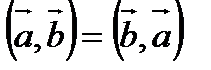
2). 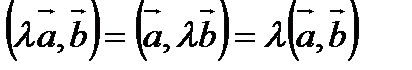
3). 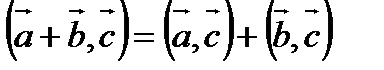
4). 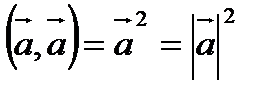
Если известны координаты векторов 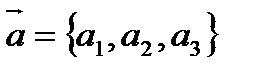 ,
, 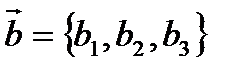 , то скалярное произведение можно найти по формуле:
, то скалярное произведение можно найти по формуле:
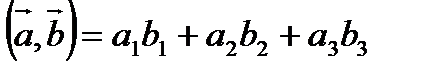
Скалярный квадрат вектора вычисляют по формуле:
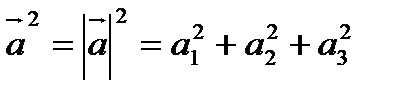
Геометрические свойства скалярного произведения:
1). 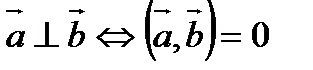
2). Если 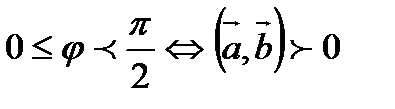 , если
, если 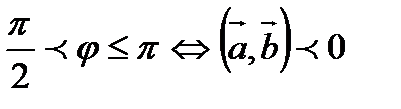
3). Формула для определения угла между векторами:
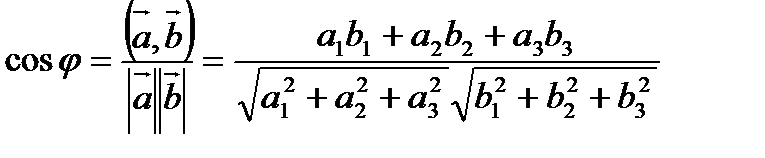
Векторное произведение.
Упорядоченная тройка некомпланарных векторов 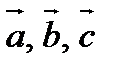 называется правой, если поворот вектора
называется правой, если поворот вектора 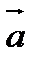 к вектору
к вектору 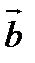 на наименьший угол в плоскости векторов
на наименьший угол в плоскости векторов 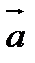 и
и 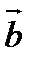 виден из конца вектора
виден из конца вектора 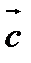 происходящим против движения часовой стрелки.
происходящим против движения часовой стрелки.
В случае, если поворот по часовой стрелке, тройка называется левой.
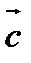
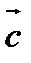
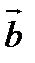
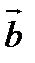
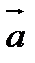
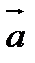
Векторным произведением 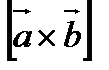 называется вектор
называется вектор 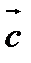 , определяемый следующими условиями:
, определяемый следующими условиями:
1). Тройка векторов 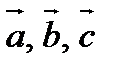 правая
правая
2). Вектор 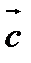 перпендикулярен
перпендикулярен 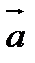 и
и 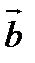
3). Длина вектора 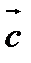 равна площади параллелограмма, построенного на векторах
равна площади параллелограмма, построенного на векторах 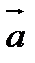 и
и 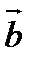 , т.е.
, т.е.
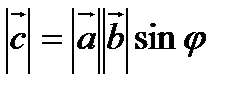
Из определения векторного произведения следует, что
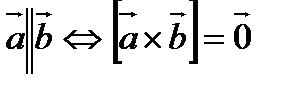
Свойства векторного произведения:
1). 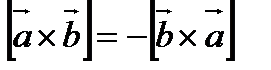
2). 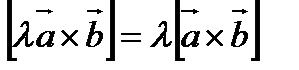
3). 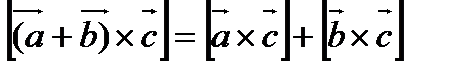
4). 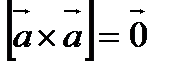
В координатной форме векторное произведение вычисляется по формуле:
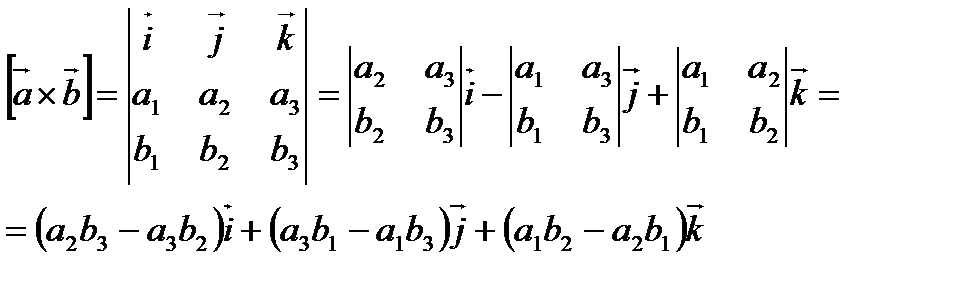
Смешанное произведение.
Смешанным произведением трёх векторов называют число равное 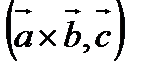 .
.
Геометрические свойства:
1). Если V – объём параллелепипеда, построенного на векторах 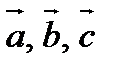 , то
, то 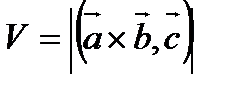 . Если
. Если 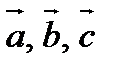 - правая тройка, то
- правая тройка, то 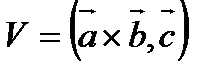 , если левая, то
, если левая, то 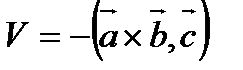 .
.
2). Вектора 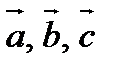 компланарны тогда и только тогда, когда их смешанное произведение равно 0.
компланарны тогда и только тогда, когда их смешанное произведение равно 0.
Основное алгебраическое свойство смешанного произведения состоит в том, что циклическая перестановка не меняет его величины, т.е.
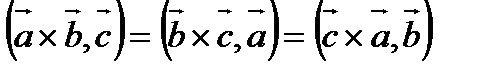
Это свойство позволяет ввести обозначение:
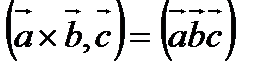
(результат не зависит от того, как расставить скобки в правой части)
Смешанное произведение через координаты записывается в виде:
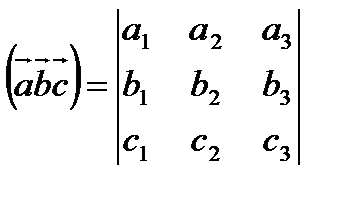
Примеры:
1. Доказать, что векторы 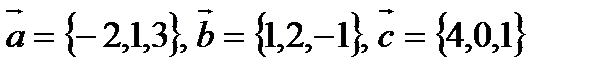 образуют базис и найти разложение вектора
образуют базис и найти разложение вектора 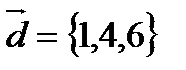 в этом базисе.
в этом базисе.
Решение: Векторы в пространстве образуют базис, если они не- компланарны. Найдём смешанное произведение этих векторов.
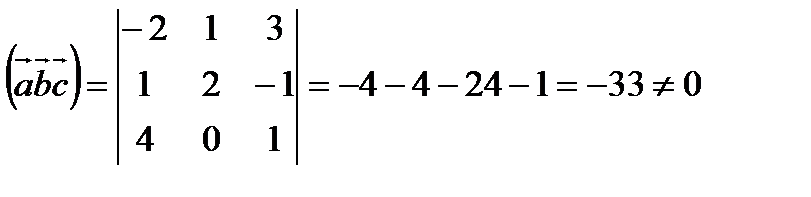
Следовательно, векторы 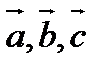 образуют базис. Пусть вектор
образуют базис. Пусть вектор 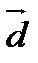 имеет в этом базисе координаты
имеет в этом базисе координаты 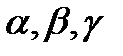 .
.
Тогда 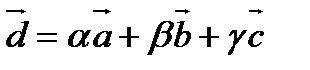 .
.
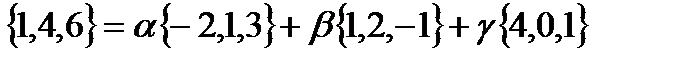
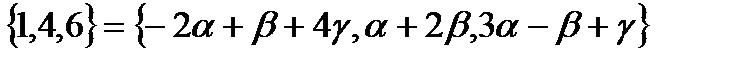
Два вектора равны, если равны их соответствующие координаты.
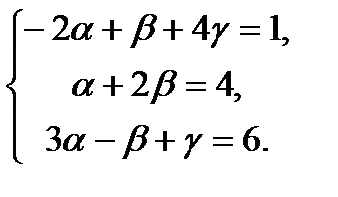
Решив эту систему, найдём 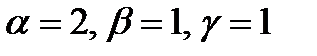 .
.
Таким образом, 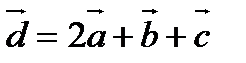 .
.
2. Даны точки 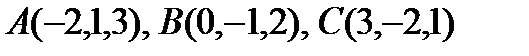 .
.
Найти: а). длину отрезка АВ,
б). 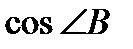 в
в 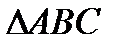 ,
,
в). 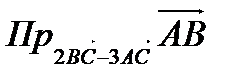 ,
,
г). направляющие 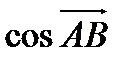 и единичный вектор направления
и единичный вектор направления 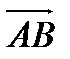 .
.
Решение: а). 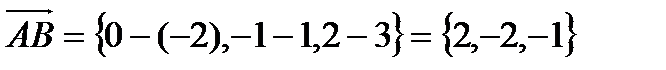
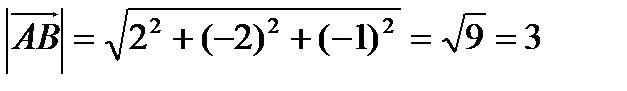
б). угол B в  есть угол между векторами
есть угол между векторами  и
и  .
.
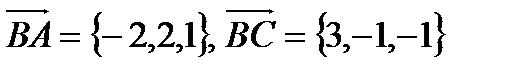
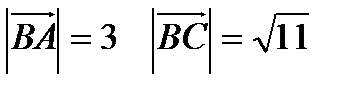
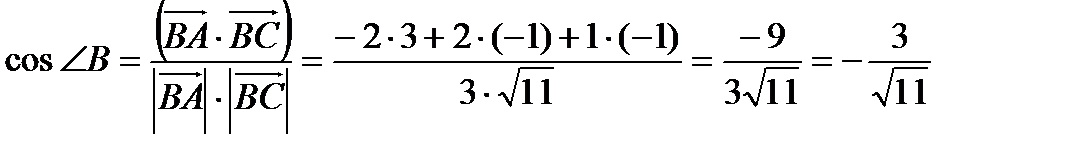
в). 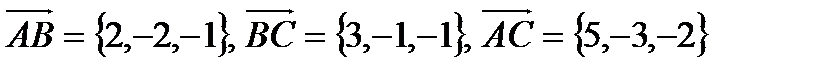
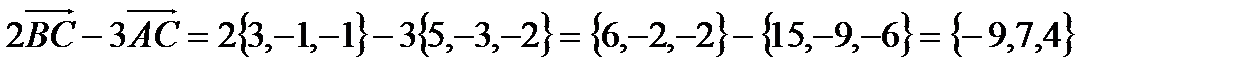
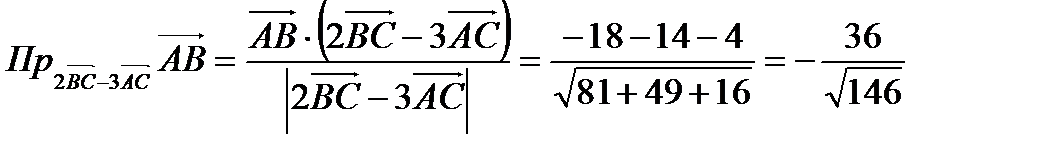
г). 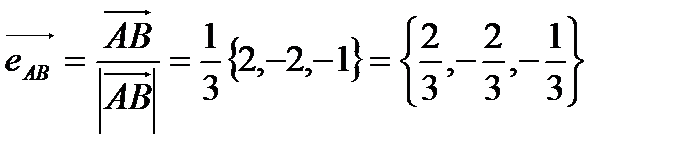
Направляющие 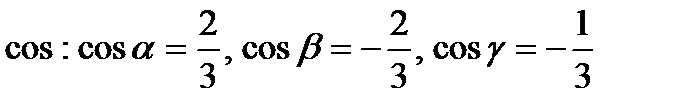 .
.
3. Найти 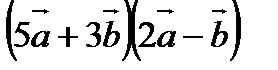 , если
, если 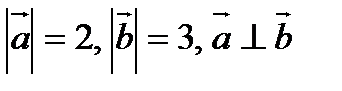 .
.
Решение: 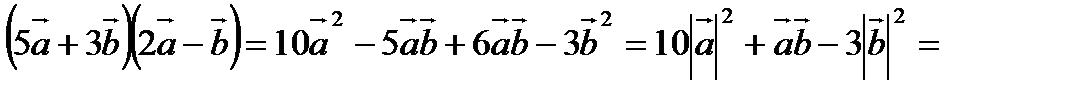
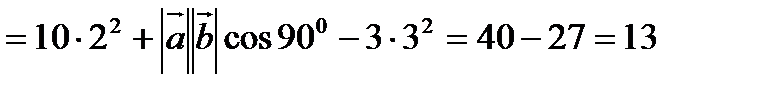 .
.
4. При каком 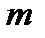 векторы
векторы 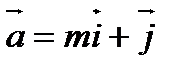 и
и 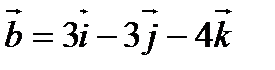 перпендикулярны?
перпендикулярны?
Решение: 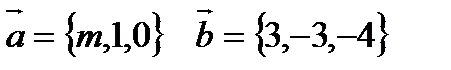
Если векторы перпендикулярны, то их скалярное произведение равно нулю.
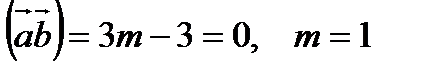 .
.
5. Найти угол между векторами 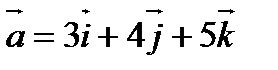 и
и 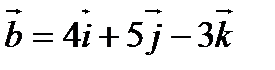 .
.
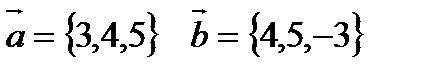
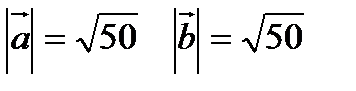
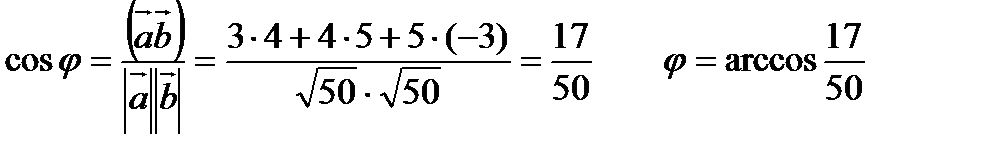 .
.
6. Найти угол между векторами 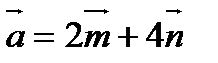 и
и 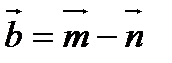 , где
, где 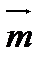 и
и 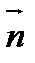 - единичные векторы и угол между ними равен
- единичные векторы и угол между ними равен 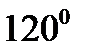 .
.
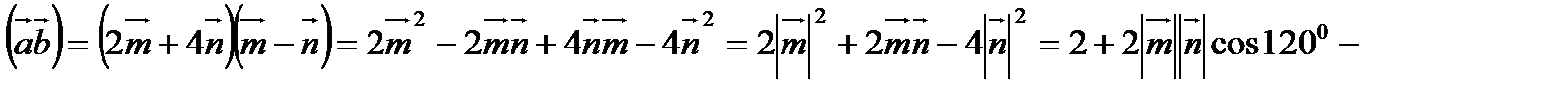
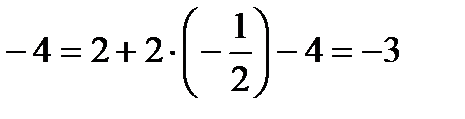
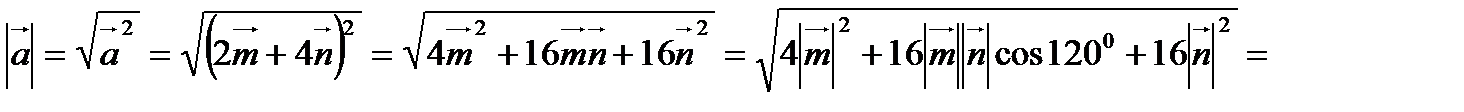
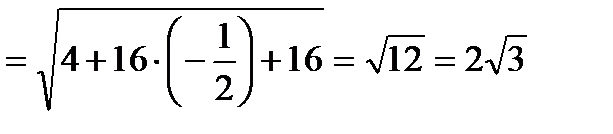
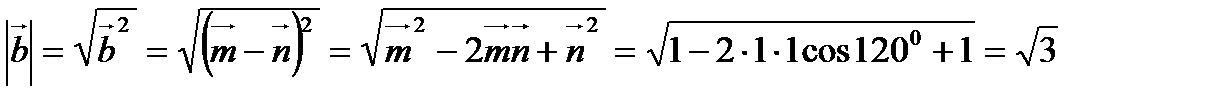
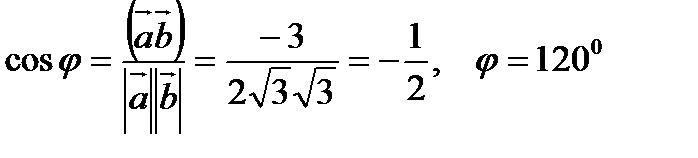 .
.
7. Найти векторное произведение векторов 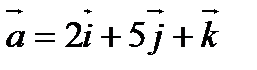 и
и 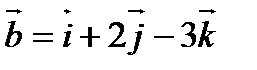
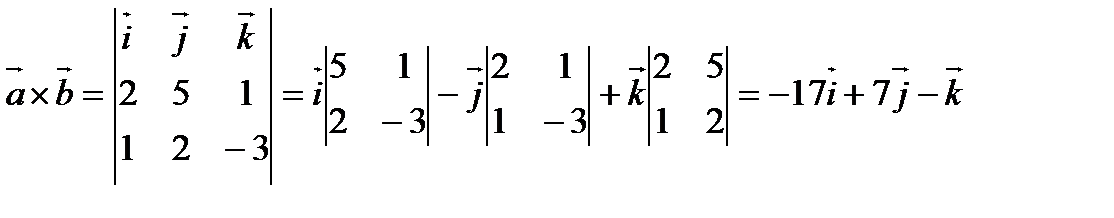 .
.
8. Вычислить площадь треугольника с вершинами 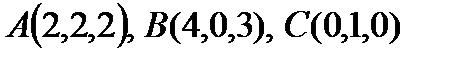 .
.
Решение: 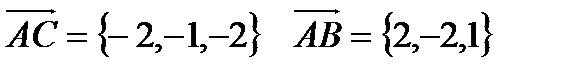
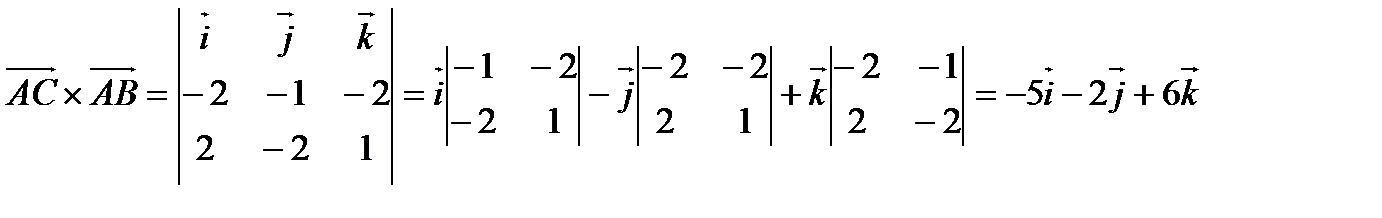
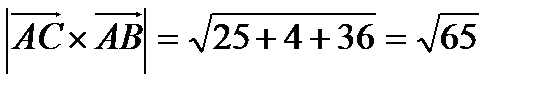
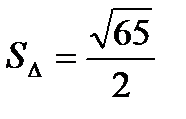 .
.
9. Найти площадь параллелограмма, построенного на векторах 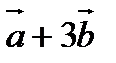 и
и 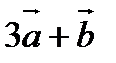 , если
, если 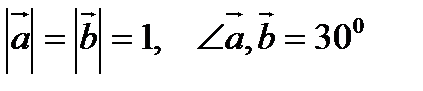 .
.
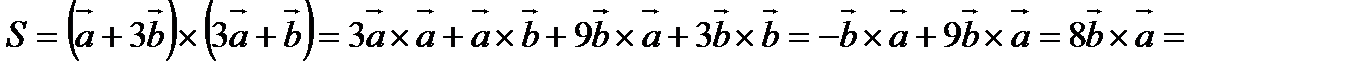
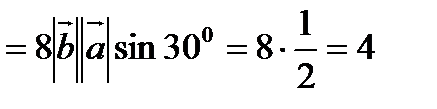
10. Даны точки 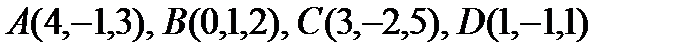 .
.
Найти: а). высоту  , опущенную из вершины А на сторону ВС;
, опущенную из вершины А на сторону ВС;
б). объём пирамиды ABCD.
а). С одной стороны 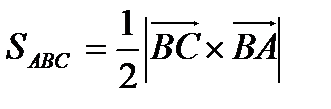 , с другой стороны
, с другой стороны 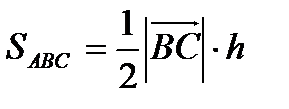 .
.
Таким образом, 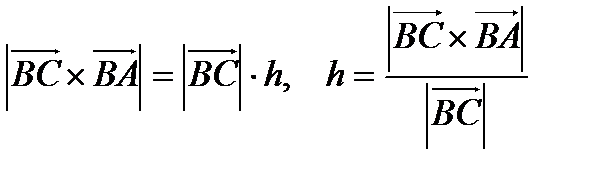 .
.
B 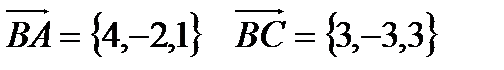
h
A C
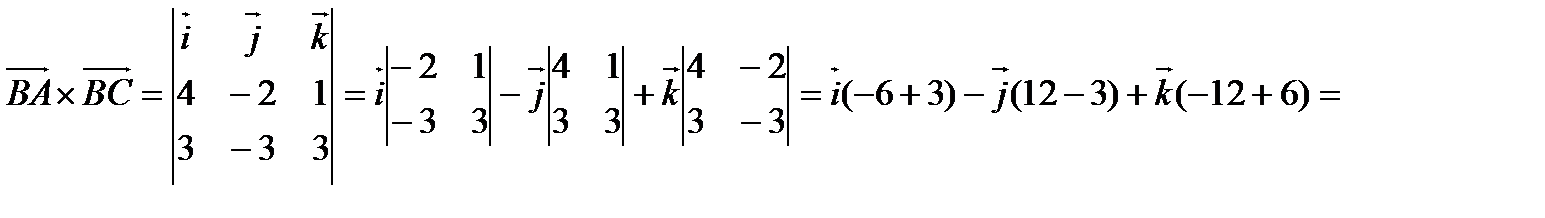
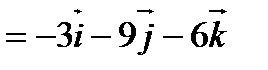
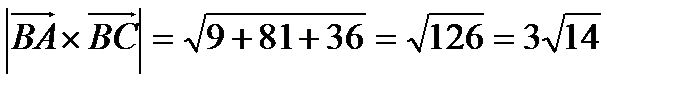
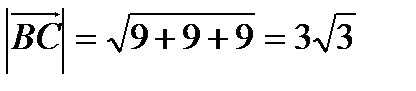
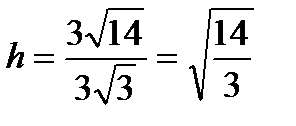
б). Объём пирамиды ABCD равен 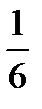 объёма параллелепипеда, построенного на векторах
объёма параллелепипеда, построенного на векторах 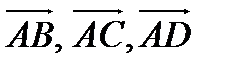 .
.
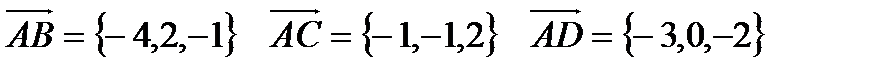 .
.
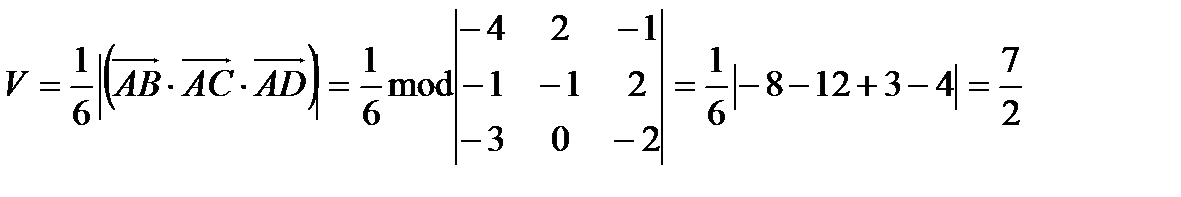 .
.
11. Доказать, что точки 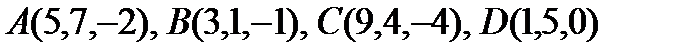 лежат в одной плоскости.
лежат в одной плоскости.
Рассмотрим векторы 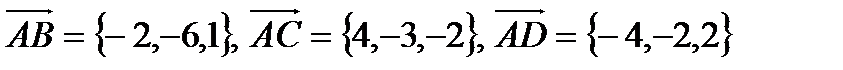 .
.
Найдём их смешанное произведение:
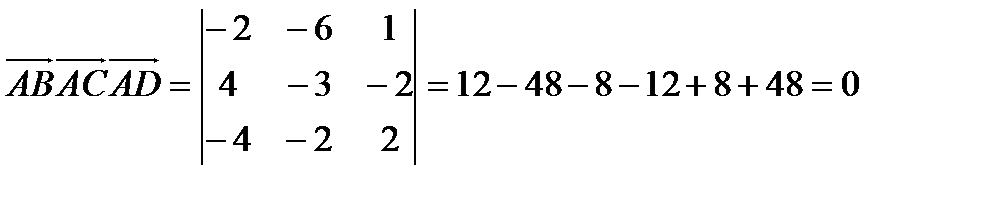
Значит, векторы компланарны, следовательно, точки A,B,C,D лежат в одной плоскости.
12. Дана пирамида, вершины которой имеют координаты: 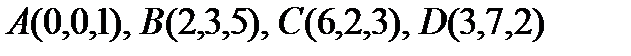 . Найти высоту, опущенную на грань BCD.
. Найти высоту, опущенную на грань BCD.
Решение: С одной стороны 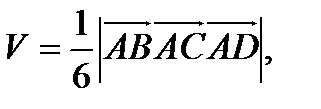 с другой
с другой 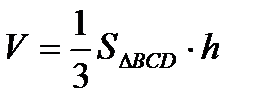 .
.
Таким образом, 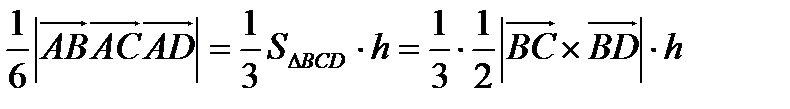 .
.
Следовательно, 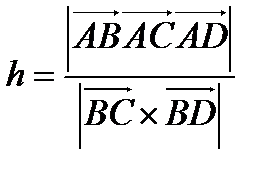 .
.
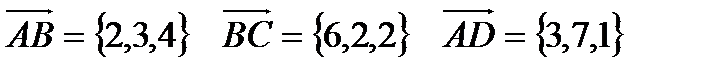 .
.
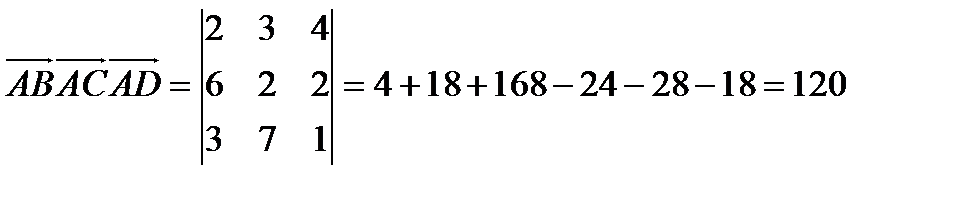
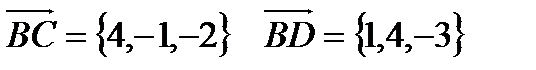
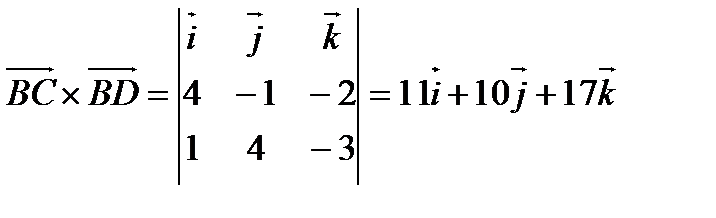
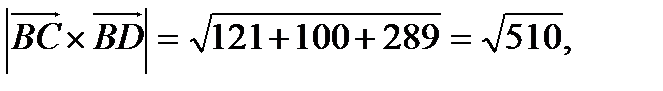
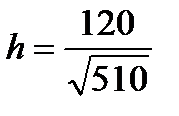 .
.
Прямая на плоскости.
Прямая на плоскости может быть задана уравнением одного из следующих видов:
1). 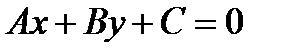 - общее уравнение прямой;
- общее уравнение прямой;
2). 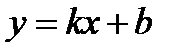 - уравнение с угловым коэффициентом.
- уравнение с угловым коэффициентом. 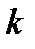 - угловой коэффициент и он равен тангенсу угла наклона прямой с положительным направлением оси
- угловой коэффициент и он равен тангенсу угла наклона прямой с положительным направлением оси 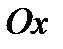 ;
;
3). 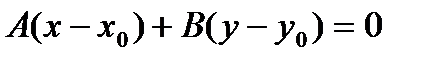 - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку 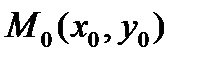 перпендикулярно нормальному вектору
перпендикулярно нормальному вектору 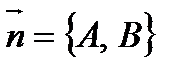 ;
;
4). 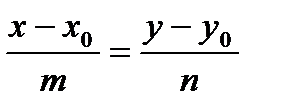 - каноническое уравнение прямой, проходящей через точку
- каноническое уравнение прямой, проходящей через точку 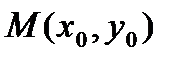 параллельно направляющему вектору
параллельно направляющему вектору 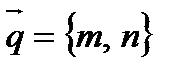 ;
;
5). 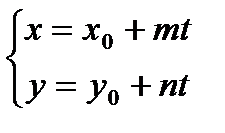 - параметрические уравнения прямой;
- параметрические уравнения прямой;
6). 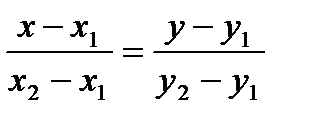 - уравнение прямой, проходящей через две точки
- уравнение прямой, проходящей через две точки 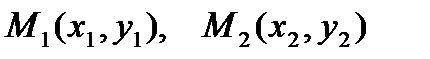 ;
;
7). 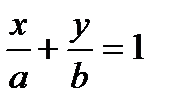 - уравнение прямой в отрезках на осях, где a и b величины отрезков, отсекаемых прямой на координатных осях;
- уравнение прямой в отрезках на осях, где a и b величины отрезков, отсекаемых прямой на координатных осях;
8). 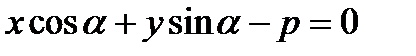 - нормальное уравнение прямой, где
- нормальное уравнение прямой, где 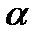 - угол, который образует нормальный вектор, направленный из начала координат к прямой, p – расстояние от начала координат до прямой.
- угол, который образует нормальный вектор, направленный из начала координат к прямой, p – расстояние от начала координат до прямой.
Общее уравнение (1) приводится к нормальному виду путём умножения на нормирующий множитель:
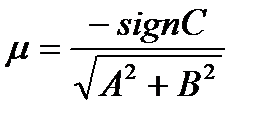 .
.
Если прямая l задана нормальным уравнением, а 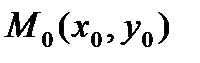 - некоторая точка плоскости, то выражение:
- некоторая точка плоскости, то выражение: 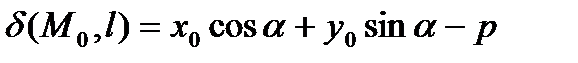 называется отклонением точки
называется отклонением точки 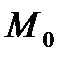 от прямой l.
от прямой l.
Знак 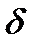 указывает на взаимное расположение точки
указывает на взаимное расположение точки 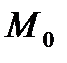 , прямой l и начала координат. Если точка
, прямой l и начала координат. Если точка 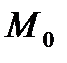 и начало координат лежат по разные стороны от прямой l, то
и начало координат лежат по разные стороны от прямой l, то 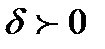 , а если по одну, то
, а если по одну, то 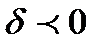 . Расстояние от точки
. Расстояние от точки 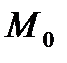 до прямой l находится по формуле:
до прямой l находится по формуле:
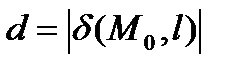 .
.
Угол между двумя прямыми.
1). Пусть заданы две прямые:
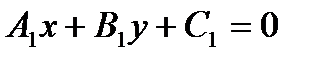 и
и 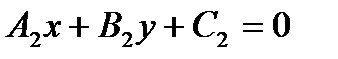
Нормальные векторы прямых имеют координаты:
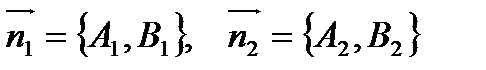
Угол между прямыми можно найти как угол между нормальными векторами:
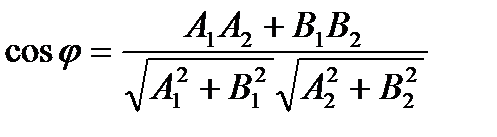 .
.
Условие параллельности двух прямых:
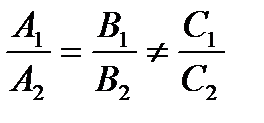 .
.
Условие перпендикулярности:
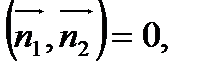 т.е.
т.е. 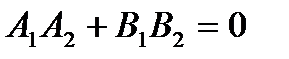 .
.
2). Если прямые заданы каноническими уравнениями:
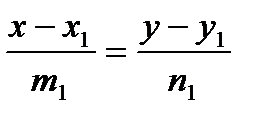 и
и 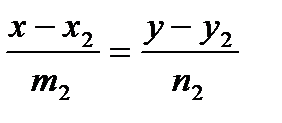 ,
,
то их направляющие векторы: 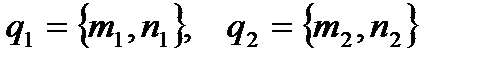 .
.
Аналогично с п.1). имеем:
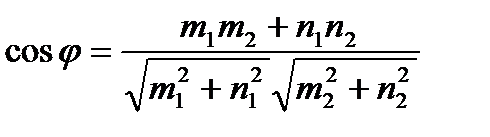
Условие параллельности:
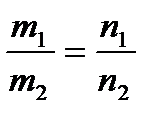 .
.
Условие перпендикулярности:
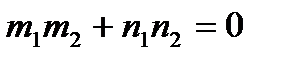 .
.
3). Если две прямые заданы уравнениями с угловыми коэффициентами:
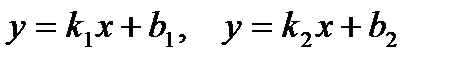 ,
,
тогда угол между прямыми можно вычислить по формуле:
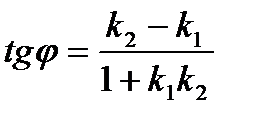 ,
,
при этом угол 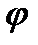 отсчитывается в направлении от первой прямой ко второй.
отсчитывается в направлении от первой прямой ко второй.
Условие параллельности:
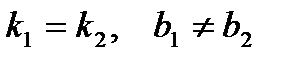 .
.
Условие перпендикулярности:
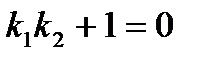 .
.
Примеры:
1. Дано общее уравнение прямой: 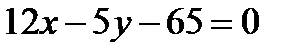 . Напишите различные типы уравнений этой прямой.
. Напишите различные типы уравнений этой прямой.
а). Уравнение прямой в отрезках;
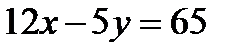
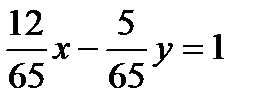
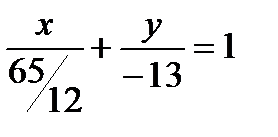
б). Уравнение прямой с угловым коэффициентом;
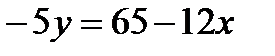
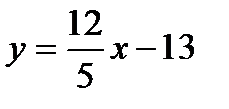
в). нормальное уравнение прямой;
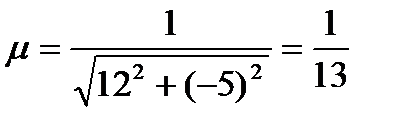
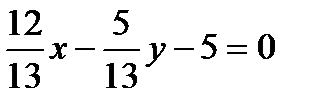 .
.
2. Найти уравнение прямой, проходящей через точку 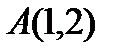 перпендикулярно вектору
перпендикулярно вектору 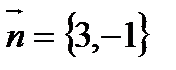 .
.
Решение: Воспользуемся уравнением 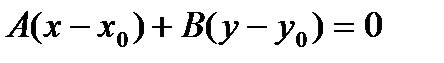
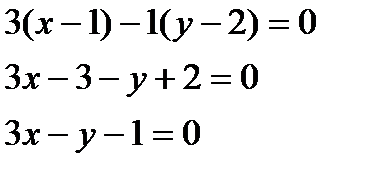
3. Составить уравнение прямой, проходящей через точку 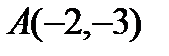 и начало координат.
и начало координат.
Решение: Уравнение прямой, проходящей через две точки имеет вид:
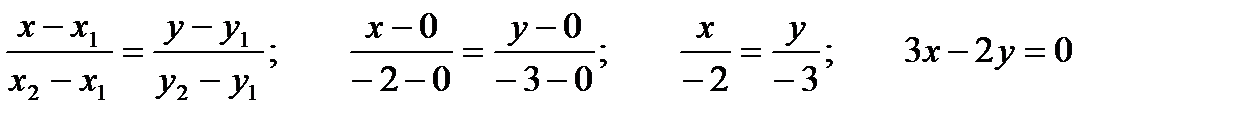
4. Написать уравнение прямой с направляющим вектором 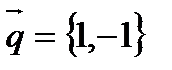 и проходящей через точку
и проходящей через точку 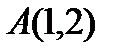
Решение: 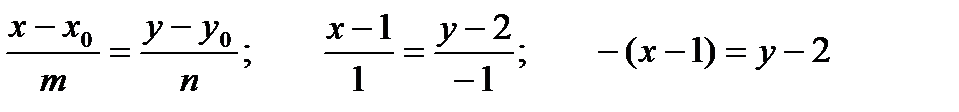
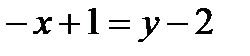
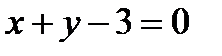
5. Найти угол между прямыми 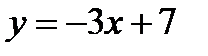 и
и 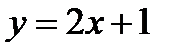
Решение: 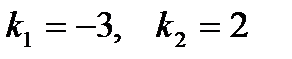
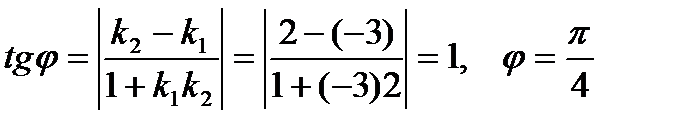
6. Показать, что прямые 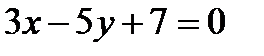 и
и 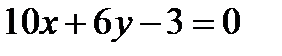 перпендикулярны.
перпендикулярны.
Решение: 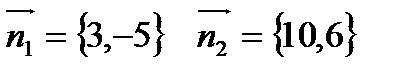
Найдём скалярное произведение 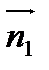 и
и 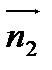
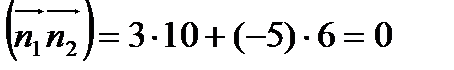 , следовательно, прямые перпендикулярны.
, следовательно, прямые перпендикулярны.
7. Даны вершины треугольника 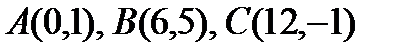 . Найти уравнения медианы, высоты, биссектрисы, проведённых из вершины С.
. Найти уравнения медианы, высоты, биссектрисы, проведённых из вершины С.
С
А Н М К В
а). медиана СМ
точка М – середина отрезка АВ.
Найдём координаты точки М:
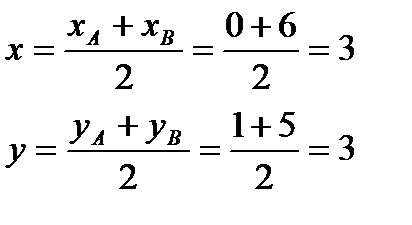
Итак, точка 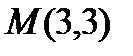
Найдём уравнение СМ как прямой, проходящей через 2 точки М(3,3) и С(12,-1)
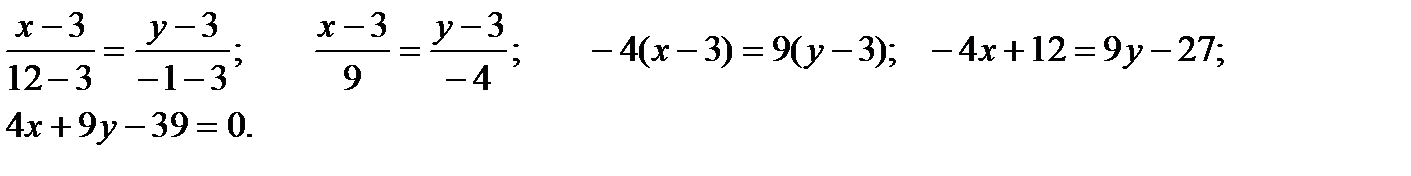
б). высота СН
Так как 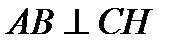 , то вектор
, то вектор 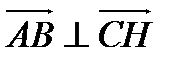 , значит он является нормальным для прямой СН, также известны координаты точки С, через которую проходит прямая СН.
, значит он является нормальным для прямой СН, также известны координаты точки С, через которую проходит прямая СН.
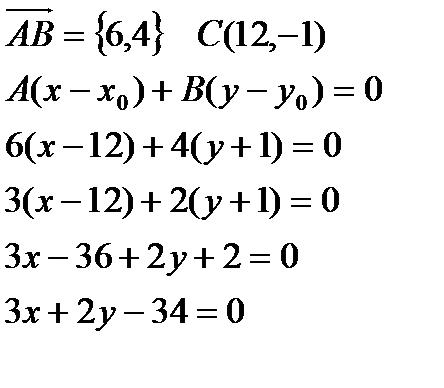
в). биссектриса СК
Воспользуемся следующим свойством биссектрисы: каждая точка биссектрисы угла равноудалена от сторон этого угла.
Возьмём на биссектрисе СК текущую точку 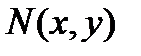 . По свойству имеем:
. По свойству имеем: 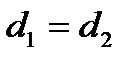 . Но
. Но 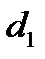 и
и 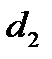 есть расстояния от точки N до АС и ВС соответственно.
есть расстояния от точки N до АС и ВС соответственно.
C
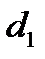
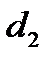
N
A K B Составим уравнения АС и ВС:
АС: 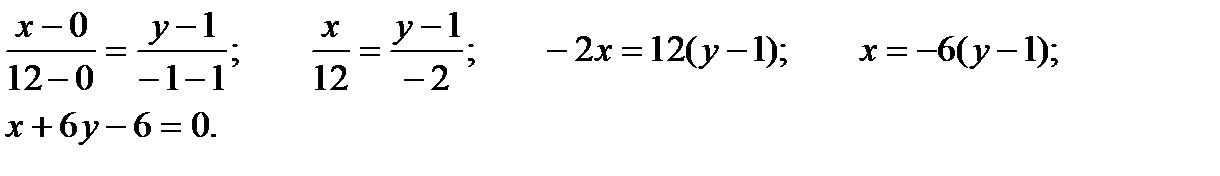
ВС: 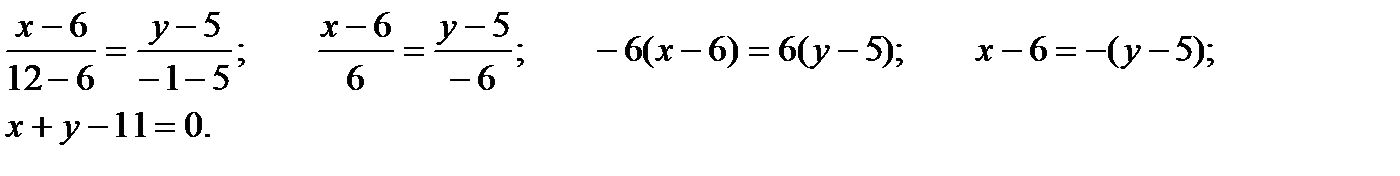
Нормируем эти уравнения:
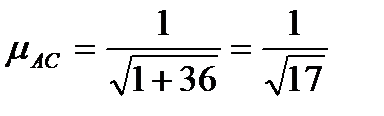 , следовательно, АС:
, следовательно, АС: 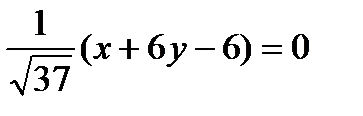 ,
,
тогда 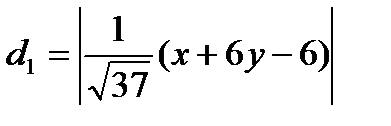 ;
;
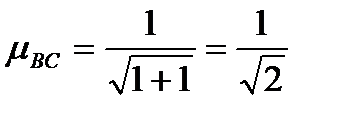 , следовательно, ВС:
, следовательно, ВС: 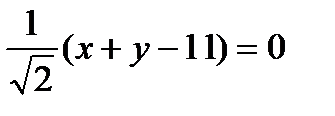 ,
,
тогда 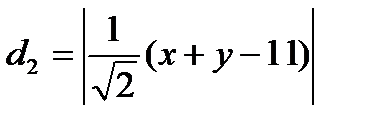 .
.
Так как 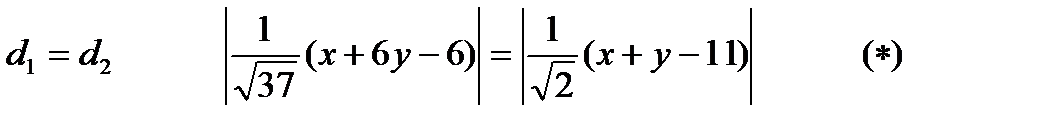
Для того, чтобы снять модули в этом соотношении, установим положение начала координат относительно прямых АС и ВС. Так как нормали 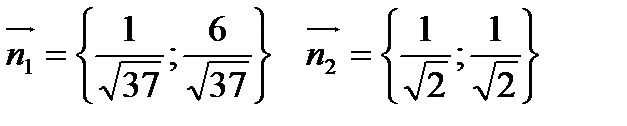 из точки О в сторону АС и ВС сонаправлены, то соотношение
из точки О в сторону АС и ВС сонаправлены, то соотношение 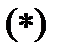 примет вид:
примет вид:
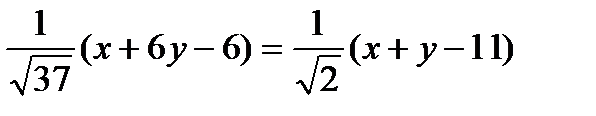
СК: 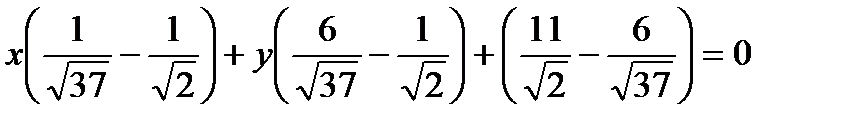 .
.
8. Составьте уравнения прямых, проходящих через точку 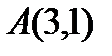 и составляющих с прямой
и составляющих с прямой 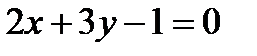 угол
угол 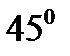 .
.
Будем искать уравнение прямой в виде 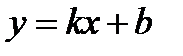 . Так как прямая проходит через точку А, то её координаты удовлетворяют уравнению прямой, т.е.
. Так как прямая проходит через точку А, то её координаты удовлетворяют уравнению прямой, т.е. 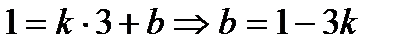 . Угол между прямыми, заданными уравнениями с угловыми коэффициентами можно найти по формуле:
. Угол между прямыми, заданными уравнениями с угловыми коэффициентами можно найти по формуле:
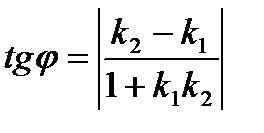 .
.
Так как угловой коэффициент данной прямой равен 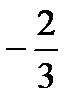 , а угол
, а угол 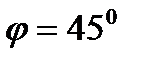 , то
, то 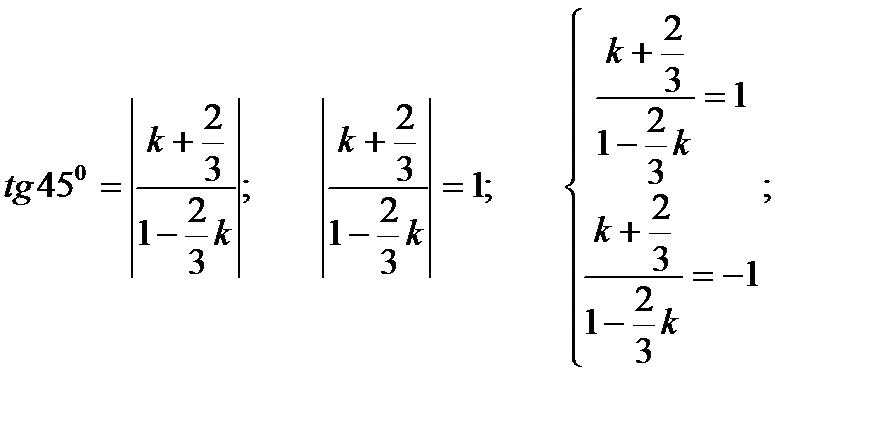
Имеем два значения k:
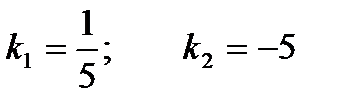 .
.
Найдём соответствующие значения b: 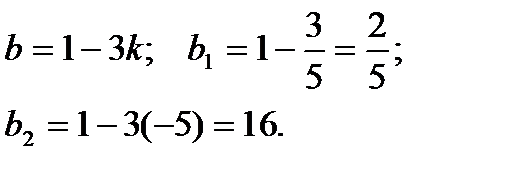
Получили две искомые прямые: 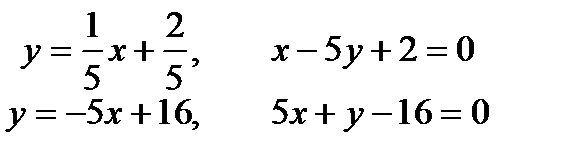 .
.
9. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного прямой и осями координат равна 8.
 Будем искать уравнение прямой в отрезках
Будем искать уравнение прямой в отрезках
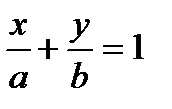 , так как
, так как 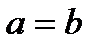 , то
, то 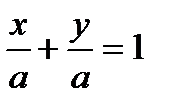
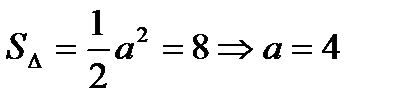
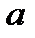
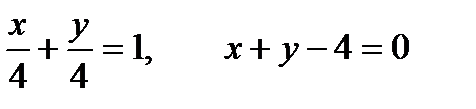

10. При каких значениях параметра t прямые 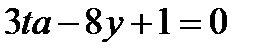 и
и 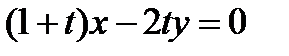 параллельны?
параллельны?
Прямые, заданные общими уравнениями параллельны, если коэффициенты при x и y пропорциональны, т.е.
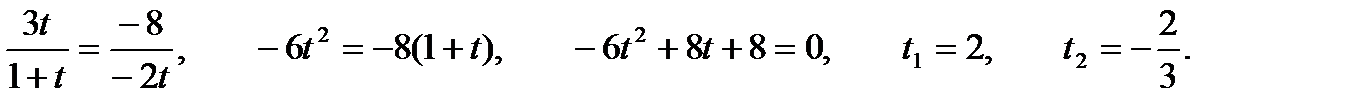
11. Найти уравнение общей хорды двух окружностей: 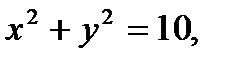
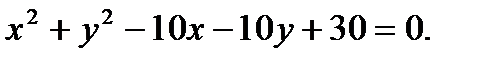
Решение: Найдём точки пересечения окружностей, для этого решим систему уравнений:
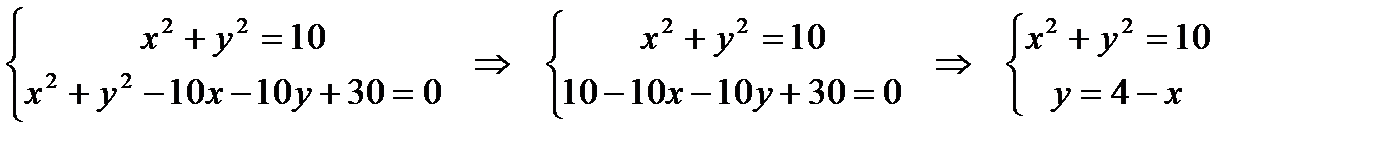
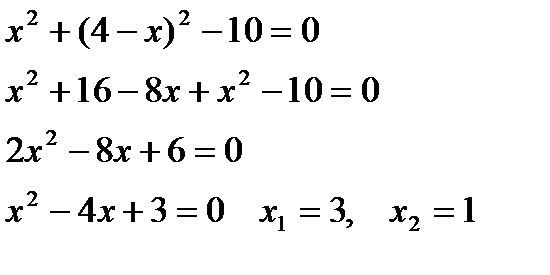
Соответственно, 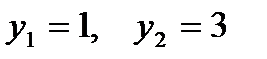 .
.
Теперь получим уравнение общей хорды, зная две точки 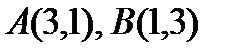 , через которые проходит эта прямая:
, через которые проходит эта прямая:
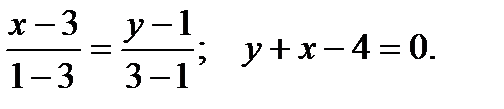
12. Найти расстояние от точки 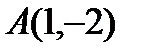 до прямой
до прямой 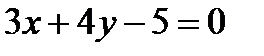 .
.
Решение: Нормируем уравнение прямой 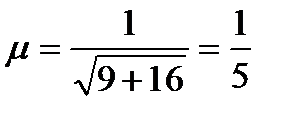 .
.
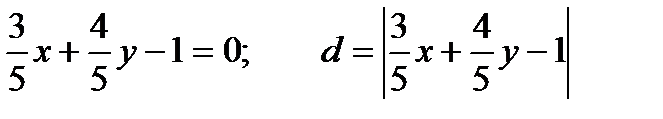
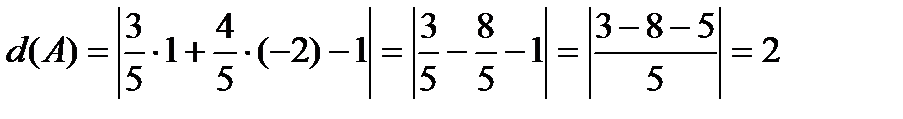 .
.
Плоскость в пространстве.
Плоскость в пространстве может быть задана одним из следующих уравнений:
1). 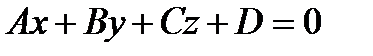 - общее уравнение плоскости;
- общее уравнение плоскости;
2). 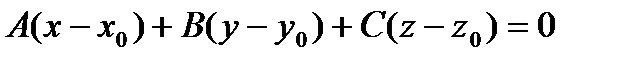 - уравнение плоскости, проходящей через точку
- уравнение плоскости, проходящей через точку 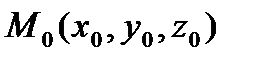 перпендикулярно нормальному вектору
перпендикулярно нормальному вектору 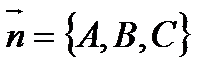 ;
;
3). 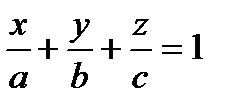 - уравнение плоскости в отрезках,
- уравнение плоскости в отрезках,  - отрезки, отсекаемые плоскостью на осях координат;
- отрезки, отсекаемые плоскостью на осях координат;
4). 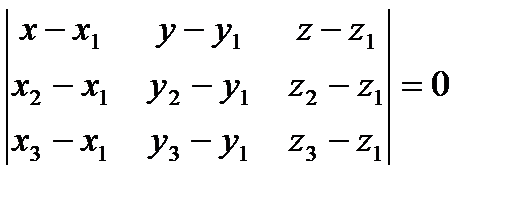 - уравнение плоскости, проходящей через точки
- уравнение плоскости, проходящей через точки 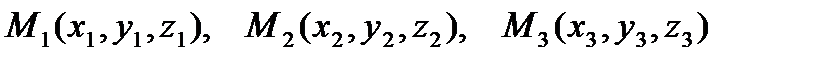 ;
;
5). 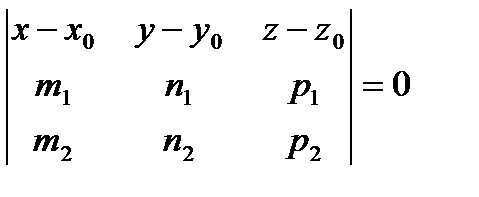 - уравнение плоскости, проходящей через точку
- уравнение плоскости, проходящей через точку 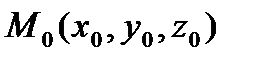 параллельно двум неколлинеарным векторам
параллельно двум неколлинеарным векторам 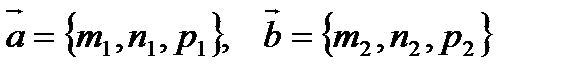 ;
;
6). 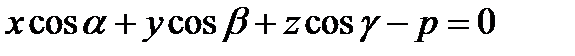 - нормальное уравнение плоскости, где
- нормальное уравнение плоскости, где 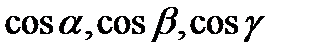 - направляющие косинусы нормального вектора
- направляющие косинусы нормального вектора 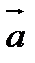 , направленного из начала координат к плоскости,
, направленного из начала координат к плоскости, 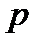 - расстояние от начала координат до плоскости.
- расстояние от начала координат до плоскости.
Общее уравнение приводится к нормальному виду умножением на нормирующий множитель
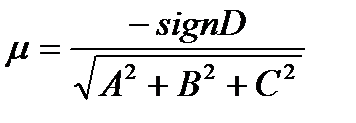 .
.
Если плоскость 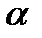 задана нормальным уравнением и точка
задана нормальным уравнением и точка 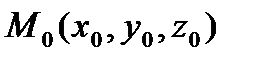 - некоторая точка пространства, то выражение
- некоторая точка пространства, то выражение 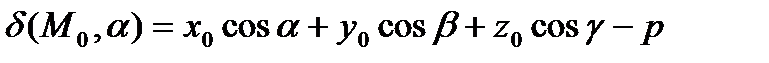 называется отклонением точки
называется отклонением точки 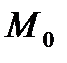 от плоскости
от плоскости 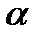 .
.
Расстояние от точки 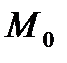 до плоскости
до плоскости 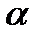 определяется равенством
определяется равенством
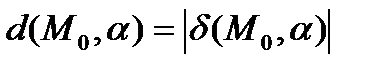 .
.
Две плоскости 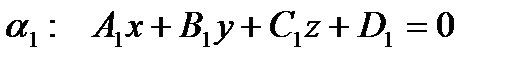 и
и 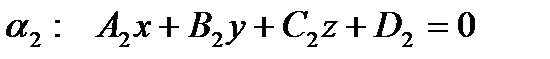 параллельны, если
параллельны, если 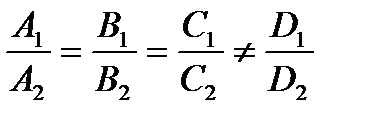 , т.е.
, т.е. 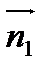 и
и 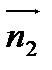 коллинеарны, перпендикулярны, если
коллинеарны, перпендикулярны, если 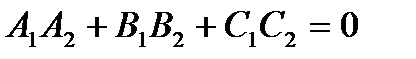 , т.е.
, т.е. 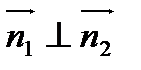 и
и 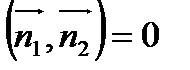 .
.
Угол между плоскостями есть угол между нормалями:
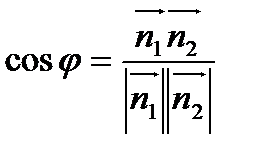 .
.
Прямая в пространстве.
Прямая в пространстве может быть задана:
1). Общими уравнениями
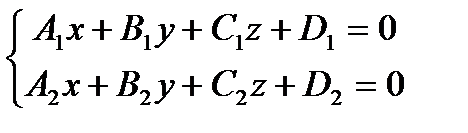 ,
,
что равносильно её заданию как линии пересечения двух плоскостей;
2). Каноническим уравнением
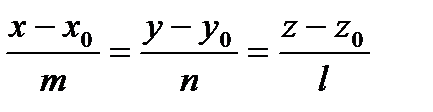 ,
,
прямая проходит через точку 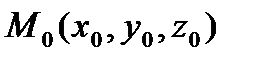 параллельно направляющему вектору
параллельно направляющему вектору 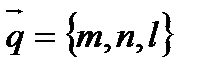 ;
;
3). Параметрическими уравнениями
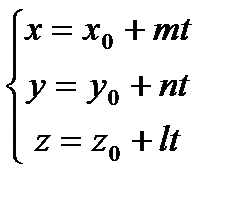 .
.
Заметим, что направляющий вектор прямой 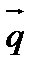 можно найти как векторное произведение нормальных векторов
можно найти как векторное произведение нормальных векторов 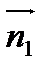 и
и 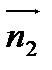 , т.е.
, т.е.
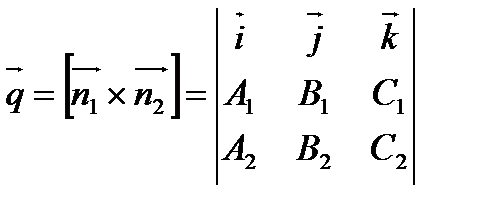 .
.
Угол между прямыми есть угол между направляющими векторами
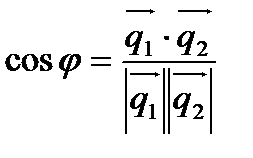 .
.
Угол между прямой 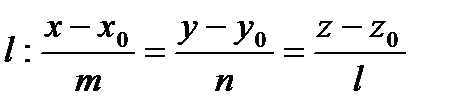 и плоскостью
и плоскостью 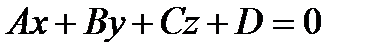 определяется по формуле:
определяется по формуле:
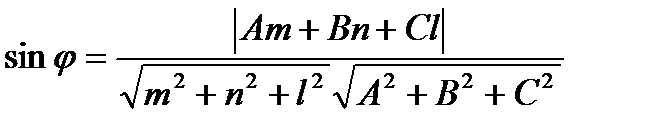 .
.
Условие параллельности прямой и плоскости: 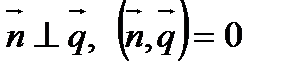
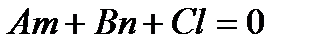 .
.
Условие перпендикулярности прямой и плоскости: 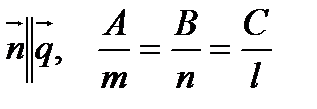 .
.
Условие принадлежности двух прямых одной плоскости. Пусть прямые заданы каноническими уравнениями:
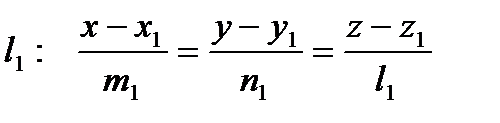 и
и 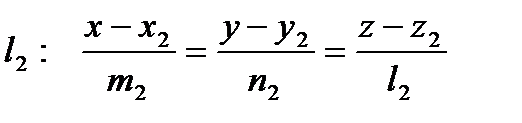 .
.
Две прямые лежат в одной плоскости, если компланарны векторы 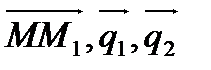 , т.е. их смешанное произведение равно 0, т.е.
, т.е. их смешанное произведение равно 0, т.е.
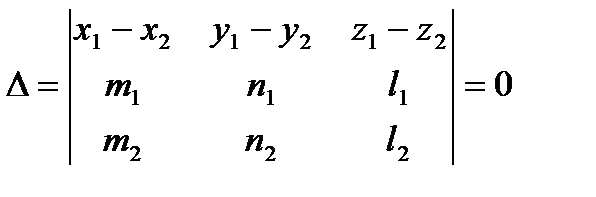 .
.
Если 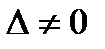 , то прямые являются скрещивающимися.
, то прямые являются скрещивающимися.
Примеры:
1. Составьте уравнение плоскости, зная что точка 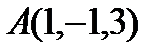 служит основанием перпендикуляра, проведённого из начала координат к этой плоскости.
служит основанием перпендикуляра, проведённого из начала координат к этой плоскости.
Решение: По условию задачи вектор 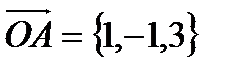 является нормальным вектором плоскости и точка
является нормальным вектором плоскости и точка 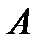 принадлежит плоскости.
принадлежит плоскости.
Воспользуемся уравнением:
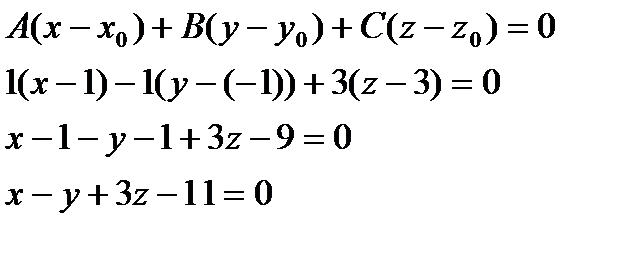
2. Найти уравнение плоскости, проходящей через две точки: 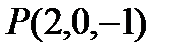 и
и 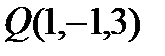 и перпендикулярной плоскости
и перпендикулярной плоскости 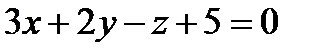 .
.
Решение: Вектор нормали к плоскости 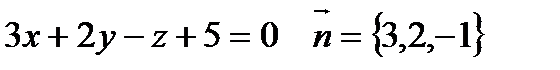 параллелен искомой плоскости.
параллелен искомой плоскости.
Выберем на плоскости текущую точку  . Векторы
. Векторы 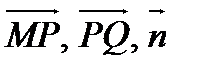 - компланарны. Тогда
- компланарны. Тогда
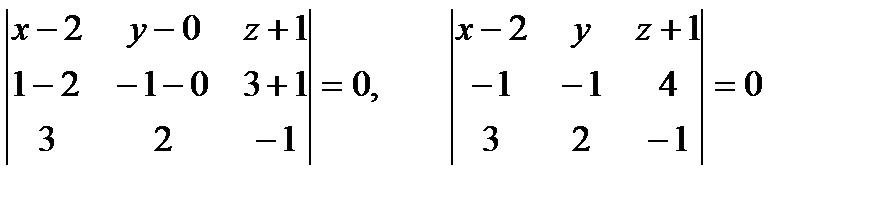
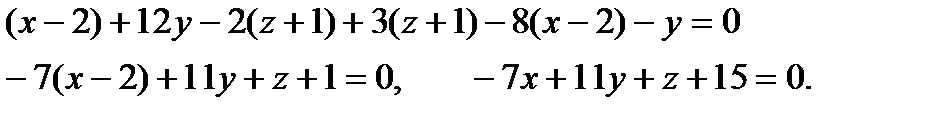
3. Составьте уравнение плоскости, проходящей через ось 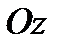 и образующей с плоскостью
и образующей с плоскостью 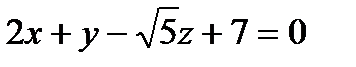 угол
угол 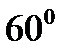 .
.
Решение: Плоскость, проходящая через ось 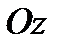 задаётся уравнением
задаётся уравнением 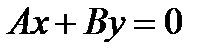 , где А и В одновременно в ноль не обращаются. Пусть
, где А и В одновременно в ноль не обращаются. Пусть 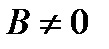 , тогда
, тогда 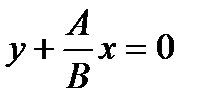 . Обозначим
. Обозначим 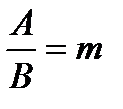 , тогда уравнение плоскости примет вид
, тогда уравнение плоскости примет вид 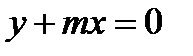 .
.
Нормальный вектор данной плоскости 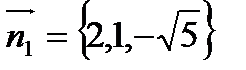 , искомой плоскости
, искомой плоскости 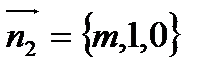 .
.
По формуле косинуса угла между двумя плоскостями имеем:
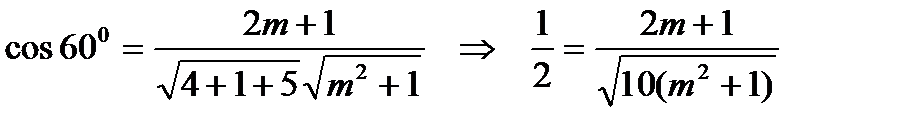
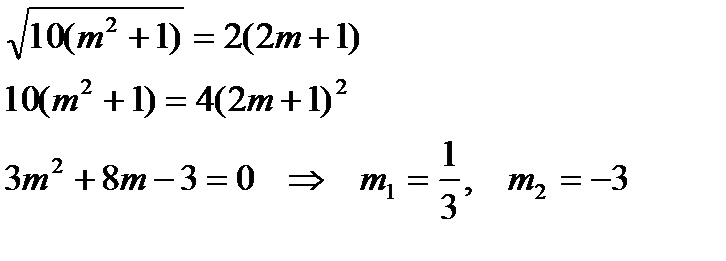 .
.
Откуда получаем две плоскости: 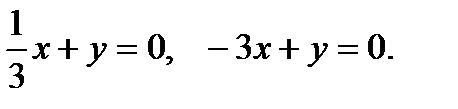
4. В пучке, определяемом плоскостями 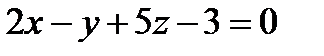 и
и 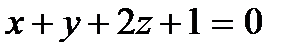 , найти две перпендикулярные плоскости, одна из которых проходит через точку
, найти две перпендикулярные плоскости, одна из которых проходит через точку 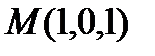 .
.
Решение: Уравнение пучка плоскостей имеет вид:
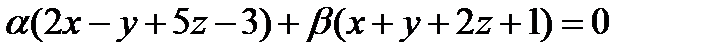 или
или
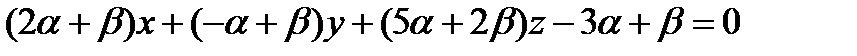 .
.
Для того, чтобы выделить из пучка плоскость, проходящую через точку М, подставим координаты этой точки в уравнение пучка
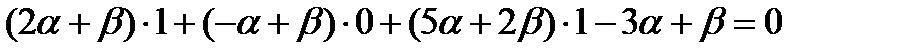
откуда имеем 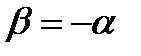 .
.
Тогда уравнение плоскости, содержащей точку М, найдём, подставив соотношение 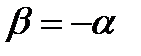 в уравнение пучка
в уравнение пучка
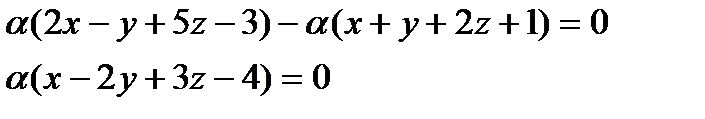
Так как 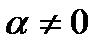 (иначе
(иначе 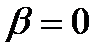 , а это противоречит определению пучка), то имеем уравнение:
, а это противоречит определению пучка), то имеем уравнение: 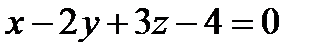 .
.
Вторая плоскость, принадлежащая пучку, должна быть ей перпендикулярна. Запишем условие ортогональности нормальных векторов:
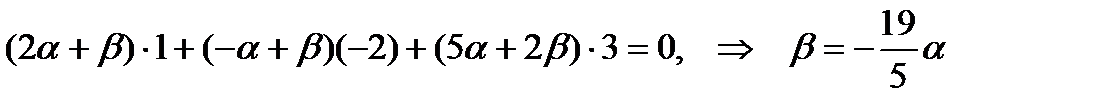 .
.
Значит, уравнение второй плоскости имеет вид:
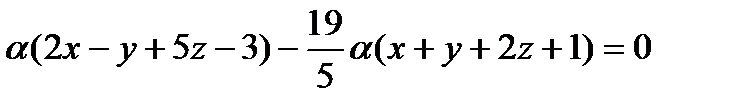
или (в силу того, что 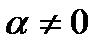 )
) 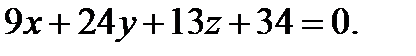
5. Даны координаты вершин пирамиды 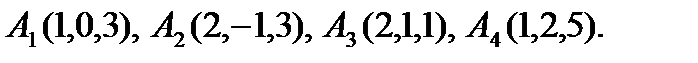
Найти угол между ребром 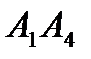 и гранью
и гранью 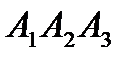 .
.
Решение: Найдём вектор нормали к грани  , как векторное произведение
, как векторное произведение 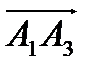 и
и 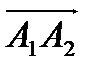 .
.
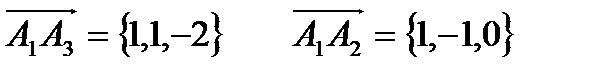
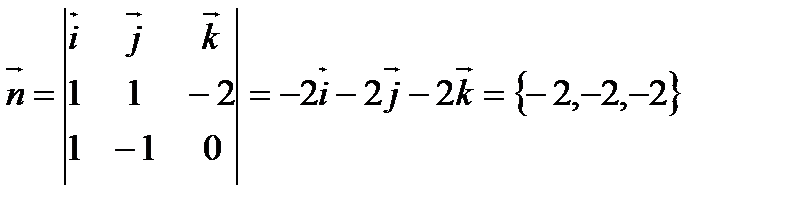
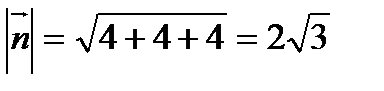 .
.
Найдём координаты вектора 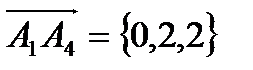 .
.
Найдём угол 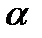 между вектором нормали и
между вектором нормали и 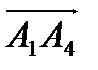 :
:
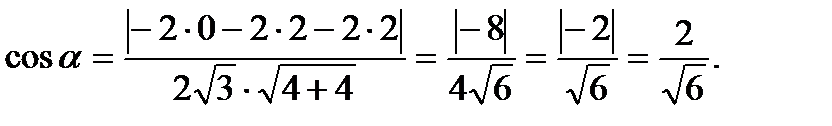
Искомый угол между вектором и плоскостью равен 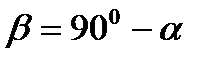 .
.
6. Даны плоскость 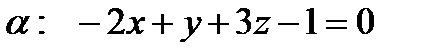 , прямая
, прямая 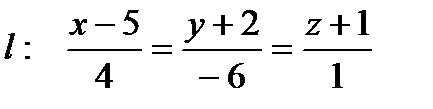 и точка
и точка 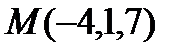 .
.
а). Составить уравнение плоскости, проходящей через точку М и параллельной плоскости 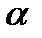 .
.
В качестве вектора нормали к искомой плоскости можно взять 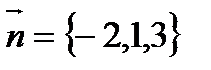 - нормаль
- нормаль 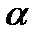 . Поэтому уравнение плоскости будет иметь вид:
. Поэтому уравнение плоскости будет иметь вид: 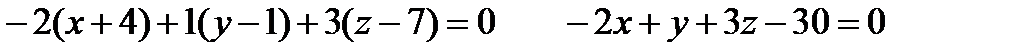 .
.
б). Составить уравнение прямой, проходящей через точку М и параллельной 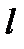 . В качестве направляющего вектора искомой прямой можно взять
. В качестве направляющего вектора искомой прямой можно взять 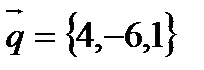 - направляющий вектор
- направляющий вектор 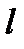 . Тогда уравнение прямой:
. Тогда уравнение прямой: 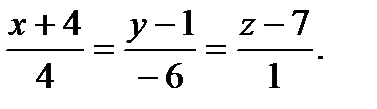
в). Составить уравнение плоскости, проходящей через точку М и перпендикулярной 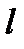 .
.
В качестве вектора нормали к исходной плоскости можно взять 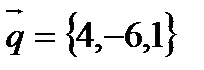 - направляющий вектор
- направляющий вектор 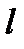 и уравнение плоскости будет
и уравнение плоскости будет 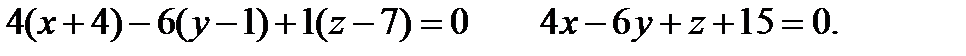
г). Составить уравнение прямой, проходящей через точку М и перпендикулярной 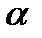 .
.
Направляющим вектором искомой прямой можно взять 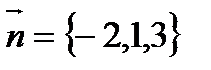 - нормаль
- нормаль 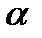 . Отсюда получим уравнение прямой
. Отсюда получим уравнение прямой 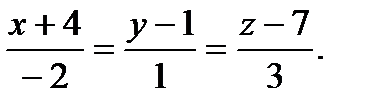
д). Составить уравнение плоскости, проходящей через точку М и прямую 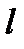 .
.
Запишем уравнение 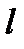 в параметрической форме:
в параметрической форме: 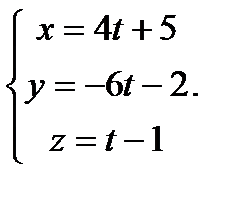 Придав
Придав 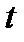 два различных значения, например,
два различных значения, например, 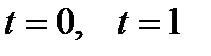 найдём две точки прямой.
найдём две точки прямой.
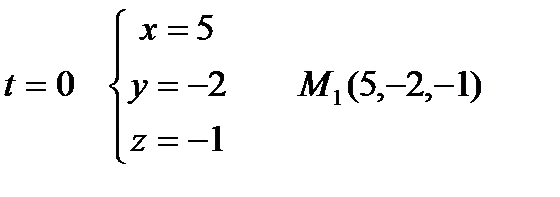
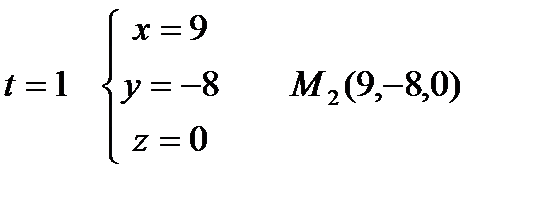
Точки  принадлежат искомой плоскости. Составим уравнение плоскости, проходящей через три точки:
принадлежат искомой плоскости. Составим уравнение плоскости, проходящей через три точки:
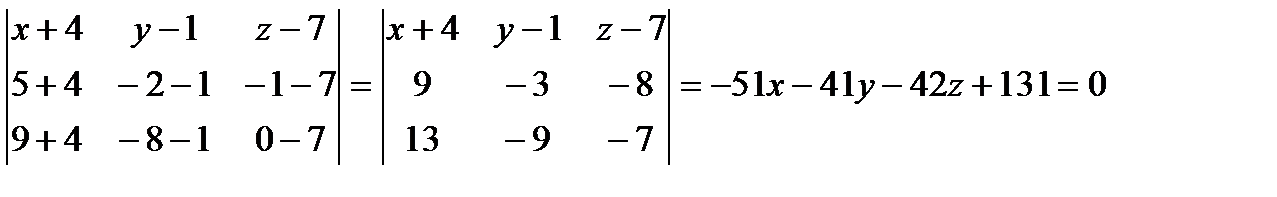 .
.
е). Составить уравнение плоскости, проходящей через точку М и перпендикулярной плоскостям 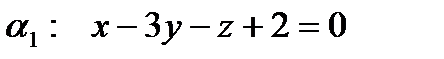 и
и 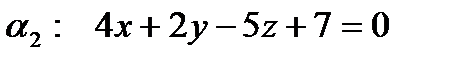 .
.
В качестве нормального вектора искомой плоскости можно взять векторное произведение 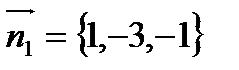 и
и 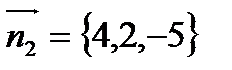 - нормальных векторов
- нормальных векторов 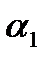 и
и 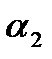 .
.
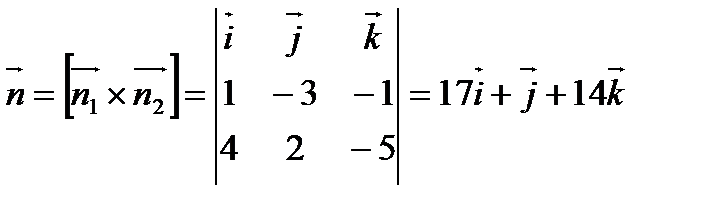 .
.
