Построение эпюр в простых рамах

Рассмотрим пример построения эпюр внутренних усилий в соответствии с планом, приведенным в предыдущем параграфе.

Пример 2.1. Построить эпюры M,Q,N (рис. 2.2, а).

Решение. В этой задаче можно не определять опорные реакции, если рассматривать равновесие части рамы, не содержащей опору.

Делим раму на участки, проводим сечения в пределах каждого из них (рис. 2.2, б) и находим искомые усилия, рассматривая равновесие соответствующих частей рамы.

На первом участке (1-2) (рис. 2.2, в):

SM_C = 0; qz₁× z₁/2 – M(z₁) = 0; M(z₁) = qz₁²/2 ;

St = 0; N (z₁) = 0 ;

Sn = 0; qz₁+Q(z₁) = 0; Q(z₁) = - qz₁.

Для определения внутренних усилий на втором участке (2-3) рассмотрим равновесие части рамы выше соответствующего сечения (рис. 2.2, г):

SM_C = 0; ql ²/2-M (z₂) = 0; M (z₂) = ql ²/2;

St = 0; ql +N(z₂) = 0; N(z₂) = - ql;

Sn = 0; Q(z₁) = 0 .

Переходя к последнему участку (3-4), будем для определенности считать, что на рис. 2.2, д z₃ < l/2. Тогда:

SM_C = 0; ql (l/2–z₃) –M (z₃)=0; M (z₃) =ql (l/2 – z₃);

St = 0; N(z₃) = 0 ;

Sn = 0; - ql + Q(z₃)= 0; Q(z₃) =ql .

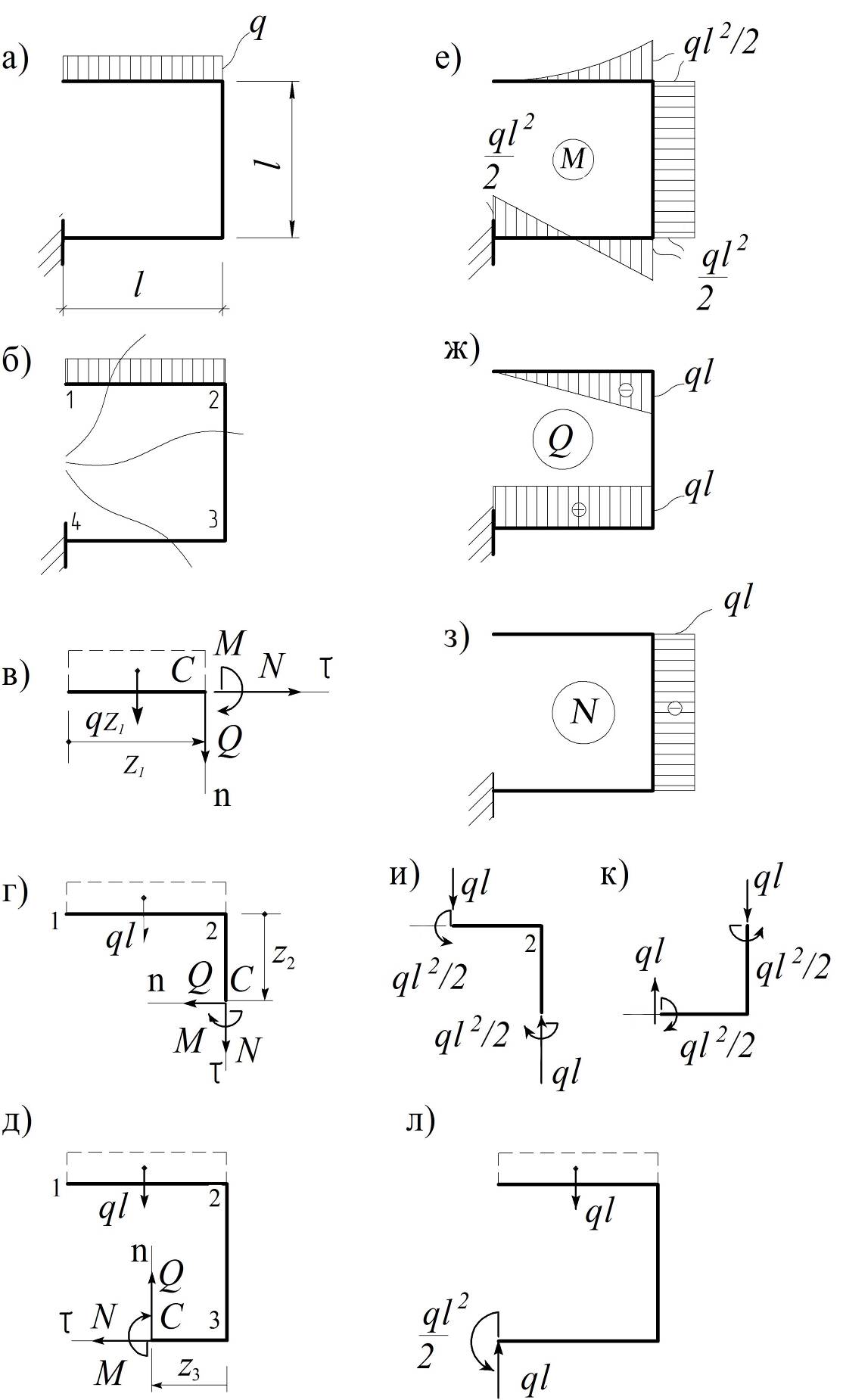
Рис.2.2

По найденным для каждого участка выражениям внутренних усилий строим соответствующие эпюры, показанные на рис. 2.2, е - 2.2, з.

Для проверки правильности построения эпюр можно рассмотреть равновесие вырезанных узлов рамы (рис. 2.2, и, к) и рамы в целом (рис. 2.2, л).

Контроль правильности построения эпюр на отдельных участках не отличается от соответствующей процедуры для балок.

Обратим внимание на следующие особенности построенных эпюр:

– при переходе через узел 2 с участка (1-2) на участок (2-3) эпюра M остается на внешних волокнах, то есть M(z₁ = l) = M(z₂ = 0);

– на участке (2-3) эпюра M = const, поскольку равнодействующая односторонних сил параллельна этому участку;

– в середине участка (3-4) эпюра M имеет нулевую точку, через которую проходит равнодействующая распределенной нагрузки. ·

Построение эпюр в рамах можно упростить, если воспользоваться стандартными эпюрами для консольной и двухопорной балок.

Например, в рассмотренном примере эпюры M и Q на участке (1-2) не будут, в соответствии с определением, отличаться от соответствующих эпюр в консольной балке, защемленной на правом конце – в точке 2.

Пример 2.2. Построить эпюры M, Q, N (рис. 2.3, а).

Решение. Определяем опорные реакции:

SX = 0; _ X_A = ql;

SM_A = 0; _ R_B = ql/2;

S M_B = 0; _ Y_A = ql/2

и делим раму на участки (рис. 2.3, б).

Эпюры M, Q, N на стойке 1-2 рамы не отличаются от соответствующих эпюр в консоли, загруженной на свободном конце найденными реакциями (рис. 2.3, в). При этом вертикальная составляющая вызывает сжатие стойки, а горизонтальная – ее поперечный изгиб.

Для построения эпюр на участке 4-3 (именно так, а не 3-4) нужно рассмотреть стойку, загруженную распределенной нагрузкой и реакцией R_B (рис. 2.3, г).

Переходим к построению эпюр на ригеле 2-3. Значения моментов на его концах известны – они находятся из условий равновесия узлов 2 и 3 и соответственно равны ql² и ql²/2, а поскольку ригель не загружен, то эпюра на нем будет линейной (рис. 2.3, д).

Поперечную силу можно найти как тангенс угла наклона касательной к эпюре моментов: Q₂₃ = ql/2, либо – по определению, как сумму проекций на вертикаль всех сил, взятых слева или справа от сечения, проведенного на этом участке (рис. 2.3, е).

Аналогично находим продольную силу N₂₃ – как сумму проекций на горизонталь всех сил, взятых по одну сторону от проведенного здесь сечения (рис. 2.3, ж).

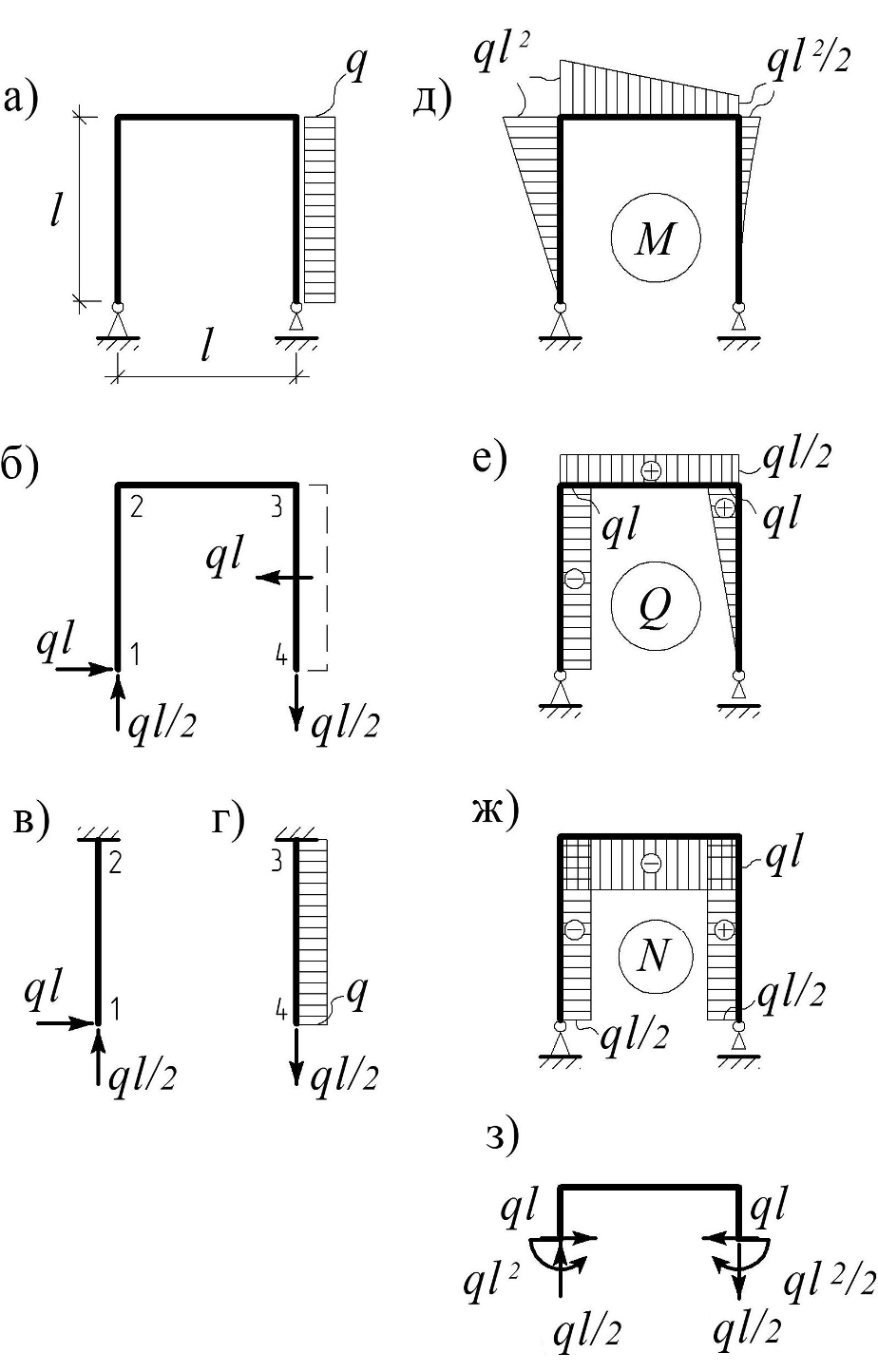
Рис.2.3

Для проверки правильности построения эпюр можно рассмотреть равновесие ригеля (рис. 2.3, з):

SX = ql – ql = 0;

SY = ql/2 – ql/2=0;

SM₂ = ql² – ql²/2 – (ql/2)·l = 0. ·

Пример 2.3. Построить эпюры M, Q, N (рис. 2.4, а).

Решение. Определяем опорные реакции и делим раму на участки (рис. 2.4, б).

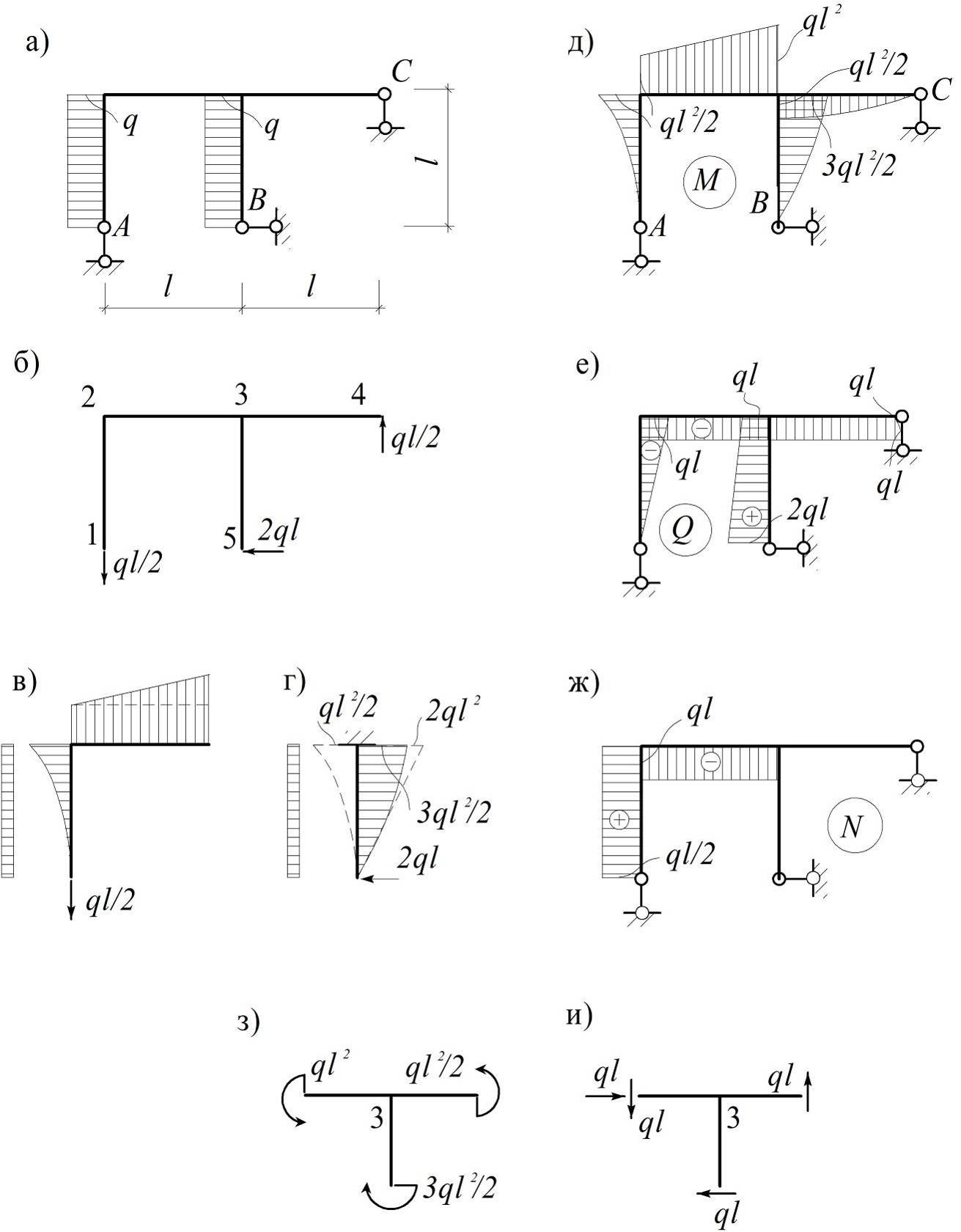
Рис. 2.4

Эпюры на участках 1-2 и 4-3 строятся по аналогии с эпюрами на участках 4-3 и 1-2 в примере 2.2.

Эпюры на участке 2-3 заданной рамы не отличаются от соответствующих эпюр в Г-образной консольной раме на рис. 2.4, в. При этом эпюру M легко построить методом суперпозиции: к эпюре от распределенной нагрузки (показана пунктиром), которая аналогична эпюре M на участке 2-3 в примере 2.1, добавляется стандартная треугольная эпюра от R_A = ql/2.

Эпюру M на участке 5-3, совпадающую с эпюрой в консоли на рис. 2.4, г, также удобно представить как сумму двух эпюр, показанных пунктиром, – от распределенной нагрузки и от реакции R_B = 2ql.

Для проверки правильности построения эпюр (рис. 2.4, д–ж) достаточно рассмотреть равновесие узла 3 (рис. 2.4, з, и). ·