Вычислить криволинейный интеграл. где – первая от начала координат арка циклоиды , .
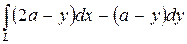
где 
– первая от начала координат арка циклоиды 
, 
.
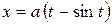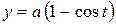КОНТРОЛЬНАЯ РАБОТА
Вариант 8
1. Вычислить интегралы:
1) 
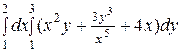
2) 
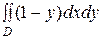, где область 
ограничена линиями: 
, 
, 
, 
.
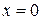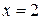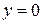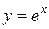3) 
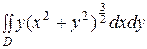, где область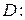 
, 
.
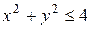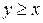2. Изменить порядок интегрирования в двойном интеграле:
1) 
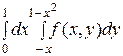2) 
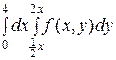
3. Вычислить площадь фигуры, ограниченной линиями: 
, 
.
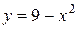Вычислить криволинейный интеграл
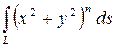
где – окружность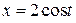 
, 
.
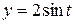Вычислить криволинейный интеграл
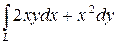
где – линия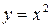 
от точки 
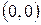до точки 
.
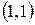КОНТРОЛЬНАЯ РАБОТА
Вариант 9
1. Вычислить интегралы:
1) 
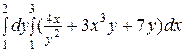
2) 
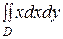, где область ограничена линиями: ,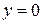 
.
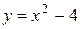3) 
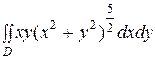, где область - кольцо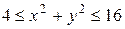 
.
2. Изменить порядок интегрирования в двойном интеграле:
1) 
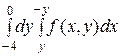2) 
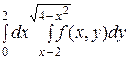
3. Вычислить площадь фигуры, ограниченной линиями: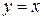 
, 
, 
.
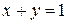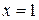4. Вычислить криволинейный интеграл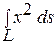 
, где – часть линии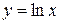 
между точками с абсциссам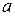и 
и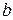 
.
Вычислить криволинейный интеграл
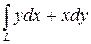
где – четверть окружности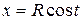 
, 
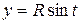от 
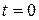до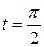 
.
КОНТРОЛЬНАЯ РАБОТА
Вариант 10
1. Вычислить интегралы:
1) 
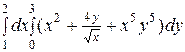
2) 
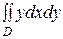, где область ограничена линиями: , 
, , 
.
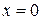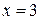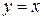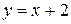3) 
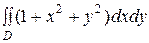, где область ограничена окружностью 
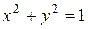и
осями координат, и расположена в первой четверти.
2. Изменить порядок интегрирования в двойном интеграле:
1) 
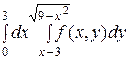2) 
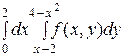
3. Вычислить площадь фигуры, ограниченной линиями: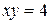 
, 
, 
.
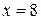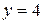Вычислить криволинейный интеграл
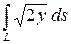
где – первая арка циклоиды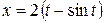 
, 
.
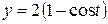Вычислить криволинейный интеграл
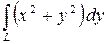
где – контур четырёхугольника с вершинами в точках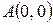 
, 
, 
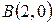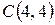и 
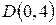, в положительном направлении.
КОНТРОЛЬНАЯ РАБОТА
Вариант 11
1. Вычислить интегралы:
1) 
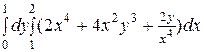
2) 
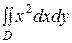, где область ограничена линиями: , , 
.
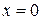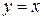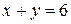3) 
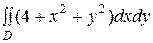, где область ограничена окружностью 
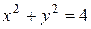и
прямыми 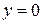и .
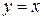2. Изменить порядок интегрирования в двойном интеграле:
1) 
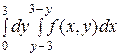2)
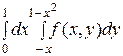
3. Вычислить площадь фигуры, ограниченной линиями: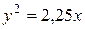 
, 
.
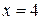4. Вычислить криволинейный интеграл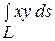 
, где – контур треугольника с вершинами А(00), В(4,0), С(4,2).
5. С помощью формулы Грина вычислить криволинейный интеграл
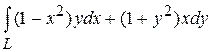
где – окружность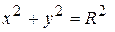 
.
КОНТРОЛЬНАЯ РАБОТА
Вариант 12
1. Вычислить интегралы:
1) 
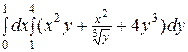
2) 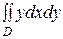, где область ограничена линиями: ,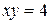 
.
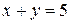3) 
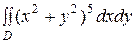, где область часть кольца между окружностям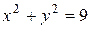и 
и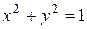 
, расположенная во второй четверти.
2. Изменить порядок интегрирования в двойном интеграле:
1) 
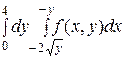2) 
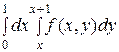
3. Вычислить площадь фигуры, ограниченной линиями: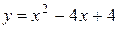 
, 
.
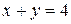4. Вычислить криволинейный интеграл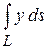 
, где –
дуга параболы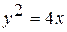 
, отсеченная параболой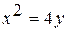 
5. С помощью формулы Грина вычислить криволинейный интеграл
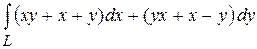
где – окружность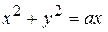 
.
КОНТРОЛЬНАЯ РАБОТА
Вариант 13
1. Вычислить интегралы:
1) 
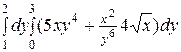
2) 
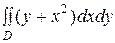, где область ограничена линиями: , ,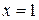 
, 
.
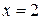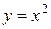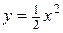3) 
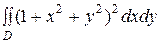, где область круговой сектор 
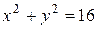, расположенный в верхней полуплоскости, между прямыми 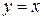и 
.
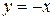2. Изменить порядок интегрирования в двойном интеграле:
1) 
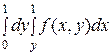2) 
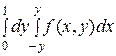
3. Вычислить площадь фигуры, ограниченной линиями: , , .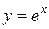
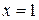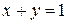4. Вычислить криволинейный интеграл
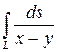
где – отрезок прямой 
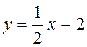, заключённый между точкам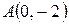и 
и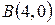 
.
5. Вычислить криволинейный интеграл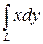 
где – контур треугольника, образованного осями координат и прямой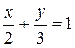 
, в положительном направлении.
КОНТРОЛЬНАЯ РАБОТА
Вариант 14
1. Вычислить интегралы:
1)
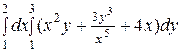
2) 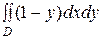, где область ограничена линиями: , , , .
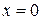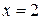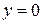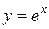3) 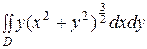, где область , .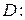
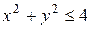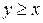2. Изменить порядок интегрирования в двойном интеграле:
1) 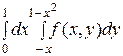2)
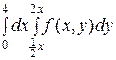
3. Вычислить площадь фигуры, ограниченной линиями: , .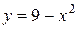