Тема 1. Предел и непрерывность функции

§1. Множество действительных чисел. Понятие функции. Способы задания функций. Элементарные функции. Простейшие неэлементарные функции.

Литература: [1, гл.5], [2, гл. 6], [3, гл.5], [4, §1.1-1.2, стр.5-9], [5, гл. 5, § 1], [7, гл.1,гл.4, §1].

Упражнения: [5,упр. 679, 700], [6 упр. 1.1. 1], 2), 5) -7), 1.2 1) -3)], [7, гл.4, упр.73,75,83,99,139,191]

§2. Числовая последовательность и ее предел. Предел функции. Основные теоремы о пределах. Бесконечно малые и бесконечно большие функции. Односторонние пределы. Два замечательных предела.

Литература: [1, гл. 6, § 4 - 10], [2, гл. 7, § 1 - 13], [3, гл. 4, § 24-28], [4, §1.2 – 1.6, cтр. 9-19], [5, гл. 5, § 2 -7, 10], [7, гл.4 § 2].

Упражнения: [5, упр. 730, 734, 736, 742, 743, 763, 770, 779, 782-785], [6, yпp. 1.20- 1.25, 136-139, 146 - 149], [7, гл.4, упр. 228, 234-241,364-267,289].

§3. Приращение функции. Непрерывность функции. Точки разрыва функции и их классификация. Свойства непрерывных функций.

Литература: [1, гл. 6, § 1 - 3], [2, гл. 8], [3, гл. 6, § 29], [4, §1.7, cтp. 19-24], [5, гл. 5, § 8], [7, гл. 4, § 2]

Упражнения: [5, yпp. 814 - 816], [6, yпp. 1.72, 1.81, 1.83, 1.86], [7, гл.4, упр. 225 - 226]

Тема 2. Дифференциальное исчисление функции одной переменной.

§1. Определение производной. Дифференцируемость и непрерывность функций. Геометрический, физический и экономический смысл. Производной. Свойства производной. Правила дифференцирования (включая производные сложной и обратной функции).

Литература: [1, гл. 7], [2, гл. 9, 10], [3, гл. 7, § 30 - 37], [4, § 1.8, 1.10,1.11, стр. 25-27, 30-40], [5, гл. 6, § 1,2,4 - 6,8­-10; гл. 7, § 1], [7, гл. 5, § 1,2].

Упражнения: [5, упр. 849, 850, 852-854, 874-877, 937-939, 980-­985, 1090-1092], [6, yпp. 2.1, 2.2, 2.7-2.17, 2.21-2.24, 2.76-­2.79, 2.111, 2.112, 2.231, 2.232], [7, гл. 5, yпp. 1, 11-13, 25-30, 33-­36, 45-50, 136, 137].

§2. Теоремы Ролля, Лагранжа, Коши. Правило Лопиталя.

Литература: [1, гл. 9, § 1], [2, гл. 11, упр. 1, 2, 5], [3, гл. 8, § 40, 41], [4, § 1.13, 1.14.1, стр. 41-45], [5, гл. 7 § 2, 3], [7, гл. 5, § 6].

Упражнения: [5, yпр. 1101-1107, 1122-1134], [6, yпp. 2.162, 2.164, 2.166-2.168, 2.171, 2.173-2.183], [7, гл. 5, § 6, yпp. 225, 234, 241, 244, 246, 260].

§3. Дифференциал функции, его связь с производной. Геометрический смысл дифференциала и его использование приближенных вычислениях. Производные и дифференциалы высших порядков.

Литература: [1, гл. 8], [2, гл. 7], [4, § 1.9, 1.12, 1.14.4, стр. 27-30, 39-40, 55-56], [7, гл. 5, § 3,4].

Упражнения: [5, yпр. 1064, 1070, 1071, 1021, 1022], [6, yпр. 2.122-2.124, 2.134-2.137, 2.146, 2.147, 2.156], [7, гл. 5, упр. 146, 160, 161, 163-167, 174, 175, 179, 198, 199].

§4. Исследование функций с помощью дифференциального исчисления. Условия возрастания и убывания функций. Экстремум функции. Необходимые и достаточные условия существования экстремума.

Литература: [1, гл. 9, § 2 -5], [2, гл. 11, § 2, упр. 3­-5, §7, yпp. 6 - 14], [3, гл. 7, § 42 - 44], [4, § 1.14.2, стр. 46-55], [5, гл. 7, § 4,5], [7, гл. 5, § 7].

Упражнения: [5, упр. 1158, 1160-1162, 1176], [6, упр. 2.203] [7, гл. 5, yпp. 282].

§5. Выпуклость графика функции. Точки перегиба и их нахождение. Асимптоты. Общая схема исследования функции.

Литература: [1, гл. 9, § 6 -8], [2, гл. XI, § 8, 10, yпp. 15 - 27], [3, гл. VП, § 45, 46], [5, гл. 7, § 6; гл. 5, §9], [7, гл. 5, § 7].

Упражнения: [6, yпp. 2.204-2.207, 2.224-2.226, 2.233, 2.234],[7, гл. 5, yпp. 297-300, 324-327].

§6. Формулы Тейлора и Мaклорена. Примеры разложения элементарных функций по формуле Маклорена.

Литература: [4, § 1;4. 14, стр. 56-57], [7, гл. 5, § 6].

Упражнения: [7, гл. 5, упр. 269-27l].

Тема 3. Дифференциальное исчисление функций нескольких переменных

Понятие функции нескольких переменных. Предел и непрерывность функции нескольких переменных. Полное и частное приращение функций. Частные производные. Дифференцируемость и дифференциал функции. Геометрический смысл дифференцируемости функций двух переменных.

Производная по направлению. Градиент и его свойства. Экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие для случая двух независимых переменных. Нахождение наибольшего и наименьшего значения функции нескольких переменных. Условный экстремум. Метод множителей Лагранжа. Метод наименьших квадратов.

Литература: [1, гл.10], [2, гл. 10], [4, гл. 3, стр. 58-72], [5, гл. 11, § 1-3, 6,11,12], [7, гл.11,12].

Упражнения: [5, 1858-1861, 1884, 1885, 1927, 1931, 1947, 2018-2025, 2030-2033, 2036, 2037], [6, 3.1, 3.4, 3.4-3.7, 3.14-3.17, 3.23-3.26, 3.29-3.33, 3.36, 3.38-3.39, 3.40-3.46, 3.51-3.53], [7, гл. 12 упр.1-4, 34, 46, 51, 59, 109-111].

Раздел 2. Интегральное исчисление.

Тема 4. Интегралы.

§1. Первообразная. Неопределенный интеграл и его свойства. Таблица интегралов. Основные методы интегрирования: замена переменной, интегрирование по частям.

Литература: [1, гл.11], [2, гл.8], [3, гл. 9], [4, §2.1-2.5, стр. 73-82], [5, гл.8, § 1-8, 10], [7, гл. 6, § 1-3]

Упражнения: [5, 1263-1267, 1279-1284, 1291-1296, 1301, 1305, 1307, 1309, 1330, 1340, 1362, 1363, 1375-1379, 1383, 1428, 1444], [6,4.1-4.5, 4.19-4.22, 4.61-4.65, 4.68-4.72, 4.80, 4.96-4.99, 4.104-4.105], [7, гл. 6 yпр. 1-5, 37-40, 56-59, 102-105, 107-110, 118, 119, 126].

§2. Определенный интеграл как предел интегральных сумм. Свойства определенного интеграла. Формула Ньютона-Лейбница. За­мена переменной и интегрирование по частям в определенном интеграле.

Литература: [1, гл.12, § 5], [2, гл. 14, § 12, упр.10], [3, гл. 10, § 59], [4, §2.6-2.9, стр. 82-88], [5, гл.9, §7], [7, гл. 6, § 4].

Упражнения: [5, 1593-1596, 1601], [6, 4.117, 4.118, 4.120-4.124, 4.129, 4.130, 4.136], [7, гл. 6 yпp. 254-257, 268-270].

§3. Геометрические приложения определенного интеграла: площадь плоской фигуры, объем тела вращения. Приближенные метод вычисления определенного интеграла: формулы прямоугольников трапеций, Симпсона.

Литература: [1, гл. 12, §6, 8], [2, гл. 15], [3, гл. Х, § 58] [4, § 2.10, 2.12, стр. 88-92, 95-97], [5, гл.9, §2-3], [7, гл. 6, §5].

Упражнения: [5, yпp. 1625, 1653, 1654, 1669, 1670], [6,4.138 4.142 - 4.146, 4.158], [7, гл.6 упр.290, 292-294, 219, 221, 388, 391]

§4. Несобственные интегралы. Понятие о кратных интегралах.

Литература: [1, гл.12, §5], [2, гл. 14, §12, упр.10], [3, гл.10, §59], [4, § 2.11, 2.13, стр. 92-95,97-99], [5, гл. IX, § 7] [7, гл. 6, § 6].

Упражнения: [5, yпp. 1748,1752], [6, упр. 4.171] [7, гл. 6 упр. 355-358].

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

ТЕМА 1.

1. Сформулируйте определение понятия функции. Что называется областью определения функции?

2. Какие функции называются элементарными?

3. Какой вид имеют графики функций у =а^Хпри а > 1, y=sin x, y=cosx, y=tg x, y=arcsin x, y=arctgx?Укажите области определения и множества значений этих функций. Какие из этих функций являются чётными?

4. При каких условиях число bназывается пределом функции f(x)при стремлении Хк числу 2, к бесконечности - ¥, + ¥? Прочитайте формулы 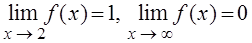и объясните их смысл.

5. Пределом какой функции при х→0 является число е?Найдите в учебнике значение числа ес двумя знаками после запятой. Как называется и обозначается логарифм числа хпо основанию к е?Какому числу равен предел ?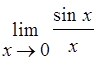

6. Какие правила применяются при вычислении пределов суммы, разности и отношения двух Функций?

7. Как определяется непрерывность функции f (х) в точке а?

ТЕМА 2.

1. Сформулируйте определение производной. Каков геометрический смысл производной?

2. Функция имеет производную в данной точке. Следует ли отсюда, что она непрерывна в этой точке?

3. Сформулируйте теоремы Ролля и Лагранжа. Каков геометрический смысл этих теорем? Сформулируйте теорему Коши.

4. В чем заключается правило Лопитaля? При каких, условиях применяется правило Лопиталя? Перечислите различные типы неопределённостей, для раскрытия которых может быть использовано это правило. Приведите примеры.

5. Что называется дифференциалом функции? Приведите примеры.

6. Каковы признаки возрастания и убывания функции?

7. Что такое экстремум функции? Каковы необходимые и достаточные условия экстремума? Приведите примеры. ­

8. Приведите пример, показывающий, что обращение производной в нуль не является достаточным условием экстремума.

9. Как найти интервалы выпуклости и точки перегиба графика функции? Приведите примеры.

Тема 3.

1. Сформулируйте определение частных производных.

2. Что называется полным приращением и полным дифференциалом функции переменных? Приведите примеры.

З. Каковы достаточные условия минимума (максимума) функции двух переменных. Что такое условный экстремум?

ТЕМА 4.

1. Сформулируйте определение первообразной функции. Докажите, что любые две первообразные одной и той же функции отличаются на константу.

2. Что называется неопределенным интегралом?

3. Какие правила применяются для вычисления неопределённого интеграла суммы функций, для вычисления òk_* f(х) dx?

4. Выведите формулу интегрирования по частям.

5. Что называется интегральной суммой функции f(x)на отрезке [а; b]. Какая фигура называется криволинейной трапецией? По какой формуле вычисляется её площадь?

6. Напишите формулу Ньютона-Лейбница.

7. Какие свойства определенного интеграла Вам известны?

8. В чём состоят определение и геометрический смысл несобственного интеграла с бесконечным пределом интегрирования?

ТЕМА 5.

1. Что называется решением дифференциального уравнения? Что является неизвестной в дифференциальном уравнении? что называется порядком дифференциального уравнения?

2. Как из общего решения дифференциального уравнения первого (второго) порядка можно получить его частное решение? Каков геометрический смысл начальных условий дифференциальных

уравнений первого и второго порядка.

3. B чем заключается смысл теоремы о существовании и единственности решения для дифференциального уравнения первого порядка? Приведите пример дифференциального уравнения первого порядка, графики двух различных решений которого пересекаются в некоторой точке. Выполнятся ли в этой точке условия теоремы существования и единственности?

4. При каких условиях дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными?

5. Как решаются дифференциальные уравнения первого порядка?

6. В каких случаях линейное дифференциальное уравнение второго порядка называется oднopoдным, неоднородным?

7. Напишите характеристический многочлен уравнения у" + b _* у' + с * у = 0.

Пусть D– дискриминант характеристического многочлена. Какой вид имеет общее решение этого дифференциального уравнения при D > 0, при D = 0 и при D < 0?

8. Какова структура общего решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами?

ТЕМА 6.

1. Что называется суммой сходящегося степенного ряда?

2. Почему при исследовании сходимости ряда можно отбрасывать любое конечное число его членов?

3. Можно ли утверждать, что ряд сходится, если предел его общего члена равен нулю?

4. Сформулируйте признак Даламбера и интегральный признак Коши сходимости ряда. Сформулируйте теорему сравнения рядов.

5. Какие знакопеременные ряды называются абсолютно сходящимися и какие - условно сходящимися? Сформулируйте признак Лейбница.

6. Приведите примеры степенных рядов, имеющих нулевой, конечный и бесконечный радиус сходимости.

7. Выпишите разложения в ряд Маклорена функций: е^х, 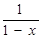, sin х, ln(l + х). Каковы области сходимости получившихся рядов?

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

ОСНОВНАЯ ЛИТЕРАТУРА:

[1]. Карасев А. Н., Аксютина 3. М., Савельева Т. Н. Курс высшей математики для экономических вузов. Ч. 1. – М.: Высшая школа, 1982.

[2]. Кудрявцев В. А., Демидович Б. П. Краткий курс высшей математики. – М.: Наука, 1989.

[3]. Маркович Э. С. Курс высшей математики с элементами теории вероятностей и математической статистики. – М.: Высшая школа,1972.

[4]. Высшая и прикладная математика. Конспект лекций. Часть I. Высшая математика. Выпуск 1. Основы математического анализа. – М.: МКУ, 1993

[5]. Минорский сборник задач по высшей математике. – М.: Наука, l986.

[6]. Зайцев М.Б., Лавриненко Т.А Высшая математика. Сборник задач, часть 1. – М.: изд. МГУК, 1998.

[7]. Шипачев В.С. Задачник по высшей математике. – М.: Высшая школа, 1998.

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА:

[8] Шипaчев В.С. Высшая математика. – М.: Высшая Школа, 1998.

[9] Данко П. Е., Попов А Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах. Ч. 1, П. – М.: Высшая школа, 1980.

[10]. Задачи и упражнения по математическому анализу для втузов./ под ред. Б.П. Демидовича. – М.: Наука, 1979.

[11]. Запорожец Г.И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1966.

[12]. Ильин В. А, Поздняк Э. Г. Основы математического анализа. Т. 1, 2. – М.: Наука, 1972.

[13]. Высшая математика для экономистов (под ред. проф. Н.М. Кремера). – М.: Банки и биржи, издательское объединение ЮНИТИ, 1998.

[14]. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. – М.: Физматгиз, 1962