Гипербола. вывод уравнения

Модуль №1. Элементы линейной алгебры и аналитической геометрии.

Тема 1.4. Элементы аналитической геометрии в пространстве и на плоскости.

Учебные вопросы:

1. Прямая на плоскости.

2. Кривые второго порядка.

Прямая на плоскости.

Среди различных уравнений прямой на плоскости наиболее распространенными можно считать следующие.

Общее уравнение прямой на плоскости имеет вид

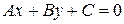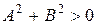, (1.1)

где A, B, C – вещественные числа (неравенство 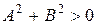означает, что коэффициенты A и B не обращаются в нуль одновременно). Вектор 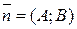называется вектором нормали и перпендикулярен данной прямой.

Уравнение прямой с угловым коэффициентом представляет собой уравнение, разрешенное относительно y:

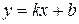. (1.2)

Здесь k – угловой коэффициент прямой (тангенс угла, который прямая образует с положительным направление оси OX).

Уравнение прямой в отрезках записывается в виде

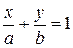, (1.3)

где a и b – соответствующие координаты точек пересечения прямой с осью OX (точка A(a;0)) и OY (точка B(0;b)).

Например, прямая 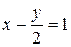проходит через точки A(1;0) и B(0;-2); прямая 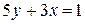через точки A(1/3;0) и B(0;1/5); (так как уравнение 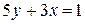равносильно уравнению .

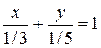Каноническое уравнение прямой имеет вид 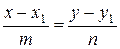, а параметрическое –

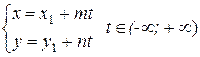, (1.4)

где 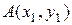- точка, лежащая на прямой, а 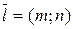- направляющий вектор прямой.

Пример 1.1. Дана прямая 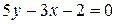. Выписать ее вектор нормали, найти угловой коэффициент, построить прямую на плоскости.

Решение. Сравнивая уравнение данной прямой с (1.2), замечаем, что в нашем случае (коэффициент при x), 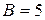(коэффициент при y), поэтому 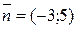. Чтобы найти угловой коэффициент, исходное уравнение необходимо разрешить относительно y:

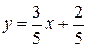; .(1.5)

Сравнивая с уравнением (1.2), замечаем, что k=3/5. Как известно, для построения прямой необходимо знать координаты двух точек, через которые проходит прямая. Задавая значения x, из (1.5) можно найти соответствующие значения y: 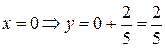; 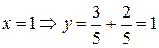. Итак, остается провести прямую, проходящую через точки A(0; 2/5), B(1; 1).

Пример 1.2. Прямая задана параметрическим уравнением 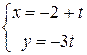. Выписать направляющий вектор данной прямой и координаты двух точек, лежащих на ней, а также координаты ее вектора нормали.

Решение. В соответствии с уравнением (1.4) 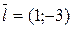, а точка A(-2;0) лежит на прямой. Чтобы найти координаты второй точки, лежащей на прямой, зададим какое-нибудь значение параметра t. В частности, при t=1 x=-1, y=-3, т.е. точка B(-1;-3) принадлежит прямой. Вектор нормали связан с общим уравнением прямой, а чтобы перейти к нему, необходимо в одном из заданных уравнений выразить t через x и полученное выражение подставить во второе уравнение. Например, из первого уравнения 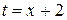, поэтому 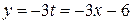. Окончательно имеем: ,

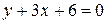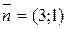
Пример 1.3. Привести к уравнению в отрезках прямую, заданную общим уравнением .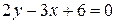

Решение.Проведем преобразования общего уравнения, чтобы привести его к виду (1.3).

.

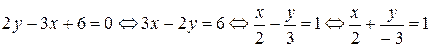Последнее уравнение и есть искомое уравнение в отрезках.

Угол j между прямыми, заданными уравнениями с угловым коэффициентом ( 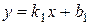, 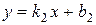), определяется с помощью формулы

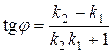. (1.6)

Из (1.6) вытекают условия параллельности( 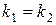) иперпендикулярности двух прямых ( ).

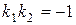Пример 1.4. Выбрать из прямых (I) – (V) параллельные и перпендикулярные, определить угол между прямыми (I) и (VI):

(I) 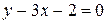; (II) 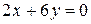; (III) ;

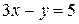(I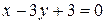V) ; (V) 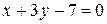; (VI) .

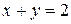Решение. Сначала для каждой прямой найдем угловой коэффициент:

(I): ;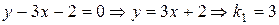

(II): ;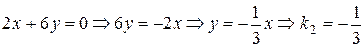

(III) ;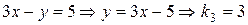

(IV) ;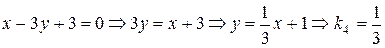

(V) ;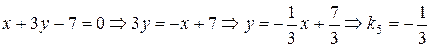

(VI) .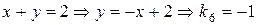

Поскольку 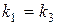, , 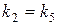получаем, что прямые (I) и (III), (II) и (V) параллельны. С другой стороны, 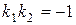, а потому прямые (I) и (II) перпендикулярны (следовательно, перпендикулярны и прямые (III) и (II), (I) и (V), (III) и (V)). Чтобы найти тангенс угла между прямыми (I) и (VI), воспользуемся формулой (8): 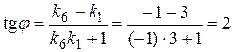. Но тогда .

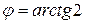Составление уравнений прямых. Рассмотрим основные типы возникающих задач.

1) Записать уравнение прямой с известным угловым коэффициентом 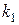, проходящей через заданную точку 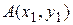. Ответом является уравнение

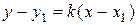. (1.7)

Пример 5. Составить уравнение прямой, проходящей через точку A(2,-3) и образующей с положительным направлением оси OX угол 120⁰.

Решение. Координаты точки известны, а угловой коэффициент 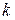- это тангенс угла наклона, т.е. 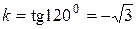. Подставляя в (1.7), получаем: 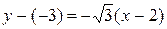или .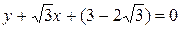

2) Записать уравнение прямой, проходящей через заданную точку 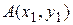параллельно прямой 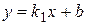. Для решения используем уравнение (1.7) и учтем, что угловые коэффициенты параллельных прямых совпадают:

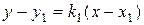. (1.8)

3) Записать уравнение прямой, проходящей через заданную точку 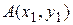перпендикулярно прямой 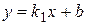. Угловые коэффициенты перпендикулярных прямых связаны соотношением 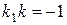, поэтому 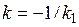. Остается подставить это в (1.8) и получить уравнение:

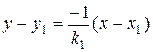. (1.9)

Пример 6. Составить уравнения прямых, проходящих через точку
A(2,-3) параллельно и перпендикулярно прямой .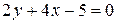

Решение. Так как 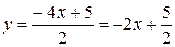, то угловой коэффициента данной прямой 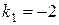. Чтобы составить уравнение прямой, проходящей через A(2,-3) параллельно данной прямой, воспользуемся уравнением (1.8): 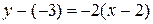или 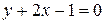. Результат можно проверить, подставив в полученное выражение координаты заданной точки: 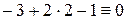(если получили тождество, как в данном примере, уравнение правильное).

Аналогично действуем при составлении уравнения перпендикулярной прямой, только используем (1.9): 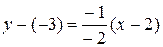, , 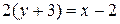и окончательно 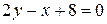. Проверка: .

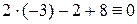4) Уравнение прямой, проходящей через две заданные точки 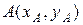, , 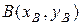имеет вид

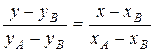. (1.10)

Пример 7. Написать уравнение прямой, проходящей через точки A(3;3), B(-1;5).

Решение. Подставляя в (1.10) координаты данных точек, получаем:

.

Собирая теперь все в одну сторону, приходим к уравнению 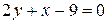. Проверить результат можно, подставляя в него поочередно координаты точек (как при проверка в примере 6): , .

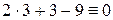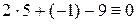Замечание. В некоторых задачах нужно найти точку пересечения заданных прямых. Для этого решают систему уравнений, задающих эти прямые.

Пример 8. В треугольнике с вершинами O(0;0), A(3;3), B(-1;5) найти уравнения стороны AB, медианы AE и высоты OK, а также длину высоты OK.

Решение. Уравнения стороны AB было получено при решении примера 6: 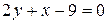.Далее, по определению медианы треугольника точка E – середина отрезка BO, поэтому ее координаты можно найти по формуле (1.3):

, .

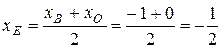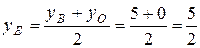Таким образом, теперь надо составить уравнение прямой, проходящей через точки A(3;3) и E(-1/2;5/2). Подставляем их координаты в (1.10):

.

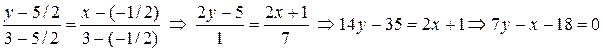Итак, уравнение медианы AE имеет вид .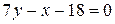

Далее, высота OK – это прямая, проходящая через вершину O перпендикулярно прямой AB. Воспользуемся уравнением (11). Угловой коэффициент прямой AB находим из уравнения 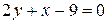: 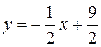, поэтому 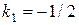. Тогда имеем: 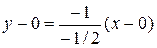, и уравнение высоты OK .

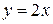Теперь найдем координаты K – точки пересечения построенной высоты и прямой AB. Решаем систему уравнений:

.

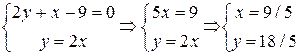Итак, 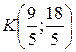. В силу (2.1b) .

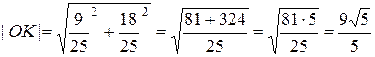Кривые второго порядка

Определение 2.1.Всякая линия, которая в некоторой системе координат описывается уравнением второй степени относительно переменных х и у, называется кривой второго порядка.

В самом общем виде уравнение кривой второго порядка таково:

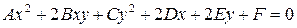(2.1)

где А, В, С, D, E, F — действительные числа, причём А, В, С одновременно не равны нулю.

Рассмотрим, прежде всего, конкретные виды кривых второго порядка и уже затем вернемся к уравнению (2.1).

ЭЛЛИПС. ВЫВОД УРАВНЕНИЯ

И ИССЛЕДОВАНИЕ ФОРМЫ

Определение 2.2. Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2a.

Для вывода уравнения эллипса введем систему координат: ось абсцисс проведем через фокусы 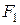и 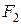, а ось ординат ‒ перпендикулярно оси абсцисс через середину расстояния между ними. Обозначим через 2с ‒ расстояние между фокусами. Тогда (рис. 1) фокусы имеют координаты 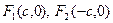. Пусть 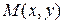‒текущая точка эллипса.

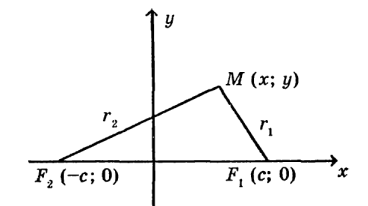
Рис. 1

Расстояние 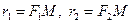называются радиусами- векторами точки и вычисляются очень просто:

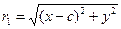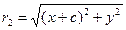, (2.2)

Из определения эллипса следует, что

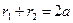, (2.3)

а простой подсчет показывает, что

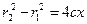(2.4)

Разделив (2.4) на (2.3), имеем:

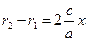. (2.5)

Складываем и вычитаем (2.3) с (2.5). Результатом являются формулы, связывающие радиус-векторы текущей точки эллипса с ее абсциссой и заданными параметрами:

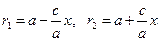(2.6)

Приравнивая 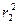в формулах (2.2) и (2.6), имеем:

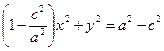(2.7)

Из условия 2а > 2с (сумма длин двух сторон треугольника больше длины третьей стороны) следует, что а > с, разность 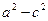- положительна. Обозначив , получаем из (2.7) :

.

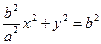После деления обеих частей равенства на 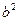, приходим к каноническому уравнению эллипса

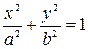(2.8)

Исследование формы и построение эллипса.

1) Если точка (х; у) лежит на эллипсе , то точка (х; -у) тоже лежит на эллипсе. Это означает, что эллипс симметричен относительно оси абсцисс. Аналогично показывается, что эллипс симметричен и относительно оси ординат.

2) Находим точки пересечения эллипса с координатными осями: при у = 0 имеем 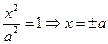. Значит, эллипс пересекает ось абсцисс в точках и 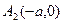. Эти точки называются вершинами эллипса. Если х = 0, то 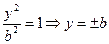, и мы отмечаем еще две вершины эллипса 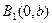и .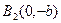

3) Выражая из уравнения эллипса у явно через х, получаем 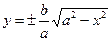. Область определения этой функции 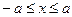, т. е. эллипс не выходит за пределы этой полосы. Рассуждая подобным образом, увидим, что эллипс не выходит и за пределы полосы 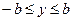. Значит, весь эллипс находится в прямоугольнике .

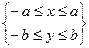4) В первом квадранте 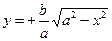. Из этого равенства следует, что с увеличением х от 0 до а, у убывает от b до 0.

Принимая во внимание все сказанное, делаем вывод о форме эллипса (рис. 2). Механически эллипс можно построить таким образом: нить длиной 2а закрепить в фокусах 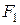и 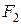, в точку М поместить острие карандаша и, натянув нить, описать точкой М эллипс.

Полагая в каноническом уравнении эллипса 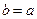, получаем окружность радиуса а с центром в начале координат. Значит, окружность ‒частный случай эллипса.

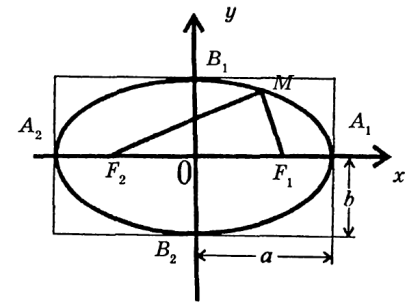
Рис. 2

ЭКСЦЕНТРИСИТЕТ ЭЛЛИПСА

Определение.Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большой оси

.

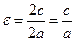Из равенства или 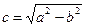следуют два важных соотношения

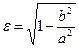и ,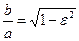

которые показывают, что эксцентриситет эллипса характеризует степень сжатия (растяжения) эллипса вдоль оси Оу: чем меньше 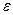, тем больше отношение 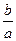и, значит, эллипс более вытянут вдоль оси Оу; минимальное значение эксцентриситета 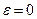соответствует тому, что 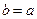, т. е. равенство нулю эксцентриситета отвечает случаю окружности. Формулы (2.6) позволяют установить связь радиусов-векторов текущей точки с эксцентриситетом:

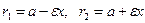. (2.9)

ГИПЕРБОЛА. ВЫВОД УРАВНЕНИЯ

Определение.Гиперболой называется геометрическое место точек, для каждой из которых разность расстояний до двух данных точек, называемых фокусами, есть величина постоянная, равная 2а.

ВЫВОД УРАВНЕНИЯ

Систему координат выбираем, как и в предыдущем случае (при выводе уравнения эллипса). Фокусы имеют те же координаты: 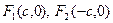, но теперь 2с>2а (длина любой их сторон треугольника больше разности длин двух других сторон) и через 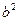обозначим величину .

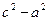Далее, для текущей точки гиперболы, расположенной справа от оси Оу, имеем (рис.3):

Рис. 3

, .

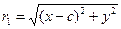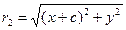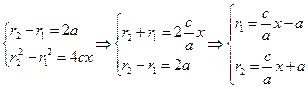
И тогда

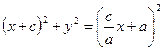
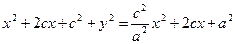
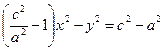
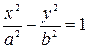(2.10)

Получили каноническое уравнение гиперболы.

Этому же уравнению удовлетворяют координаты любой точки гиперболы, расположенной слева от оси ординат.

ИССЛЕДОВАНИЕ ФОРМЫ ГИПЕРБОЛЫ

1) Если точка (х; у) лежит на гиперболе, то на гиперболе лежат точки (-х; у )и (х; -у) и (-х; -у). Это значит, что обе координатные оси являются осями симметрии, а начало координат ‒ центром симметрии гиперболы или просто ее центром. Ось абсцисс называется фокальной осью гиперболы (или действительной осью).

2) Находим точки пересечения гиперболы с осями координат. При у = 0 получаем 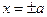. Точки и 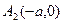называются действительными вершинами гиперболы. Если х = 0, то 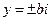. Это означает, что гипербола не имеет точек пересечения с осью Оу; тем не менее точк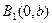и и 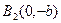имеют большое значение для построения гиперболы. Их называют мнимыми вершинами гиперболы.

3) Выразим у явно через х: 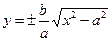. Эта функция определена тогда и только тогда, когда 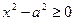, т. е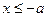. для и для . Это говорит о том, что гипербола имеет две ветви: левую и правую.

4) В первом квадранте 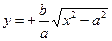. Когда 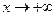то, 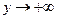, возрастая.

5) Прямая 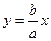является асимптотой гиперболы. Действительно,

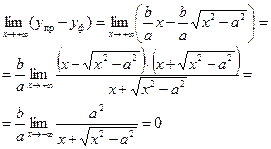
Из соображений симметрии следует, что прямая тоже является асимптотой гиперболы.

ПОСТРОЕНИЕ ГИПЕРБОЛЫ

Прежде всего, построим асимптоты гиперболы. С этой целью изобразим прямоугольник со сторонами 2а и 2b (рис. 4).

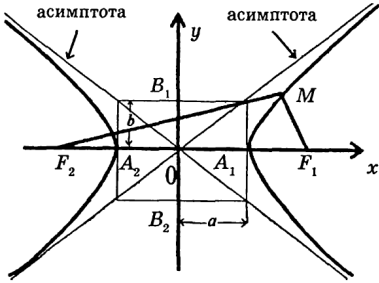
Рис. 4

Диагонали этого прямоугольника и есть асимптоты. Теперь в первом квадранте от вершины А₁ график гиперболы возрастая стремится к 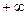, приближаясь к асимптоте. В остальных квадрантах график гиперболы строится на основе симметрии.

Если 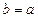, гипербола называется равнобочной.

Эксцентриситетом гиперболы называется отношение фокусного расстояния

к длине действительной оси:

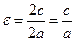
Т. к. с > а, то 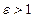( в отличие от эксцентриситета эллипса).

Из соотношения 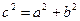следует, что

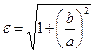и ,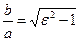

откуда ясно, что эксцентриситет характеризует степень сжатия (растяжения) гиперболы вдоль оси Оу.

ПАРАБОЛА. ВЫВОД УРАВНЕНИЯ

Параболой называется геометрическое место точек, одинаково удаленных от данной прямой, называемой директрисой и от данной точки, называемой фокусом.

Для составления уравнения параболы выбираем систему координат: ось абсцисс проводим через фокус 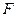перпендикулярно директрисе, ось ординат ‒ перпендикулярно оси Ох через середину расстояния р между фокусом и директрисой (рис. 5).

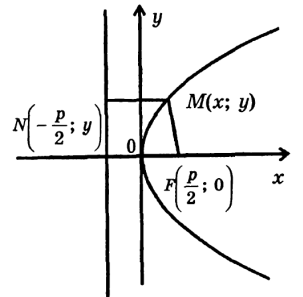
Рис. 5

Величина р называется параметром параболы.

Пусть М(х; у) ‒текущая точка параболы, 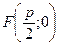‒ ее фокус, 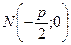‒ основание перпендикуляра, опущенного из точки М на директрису. Тогда

.

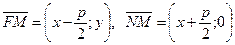По определению параболы

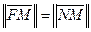
т. е.

.

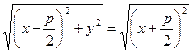Отсюда

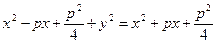
т. е.

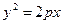, (2.11)

Это и есть каноническое уравнение параболы.

ИССЛЕДОВАНИЕ ФОРМЫ И ПОСТРОЕНИЕ ПАРАБОЛЫ

1) Если точка (х; у) лежит на параболе, то точка (х; -у) тоже лежит на параболе. Значит, парабола симметрична относительно оси Ох, т. е. ось Ох ‒ ось симметрии параболы.

2 )О(0 ; 0) ‒ единственная точка пересечения параболы с координатными осями. Эта точка называется вершиной параболы.

3) Выразив у явным образом через х, имеем:

.

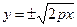Учитывая, что р > 0, делаем вывод, что область определения параболы: 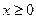. Это говорит о том, что парабола целиком расположена в правой полуплоскости.

4) Формула 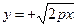(верхняя часть параболы) говорит о том, что с ростом х: от 0 до 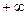у тоже растет от 0 до 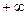. Парабола имеет вид, изображенный на рис. 5.