Бесконечно малые функции в точке. Теоремы о бесконечно малых

1) Функция 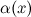называется бесконечно малой функцией (б.м.ф.) при 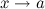(или в точке 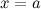), если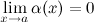

2)Теорема 1.Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.

Доказательство. Пусть 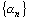– бесконечно малая последовательность. Это означает, что для любого положительного числа 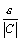существует такой номер N, что для всех номеров 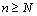выполняется условие 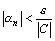, где С – любое действительное число. Тогда <

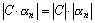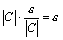< , а это и означает, что последовательность 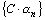– бесконечно малая.

Теорема 2.Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.

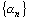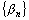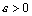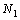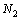Доказательство. Пусть и – бесконечно малые последовательности. Это означает, что для любого числа существуют такие номера и , что для всех номеров 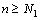и для всех номеров 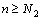выполняются условия 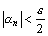и 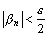соответственно. Тогда для всех номеров 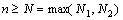выполняется условие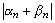 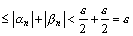, а это и означает, что последовательность 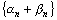– бесконечно малая.

Следствие 1. Разность двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Следствие 2. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Теорема 3. Бесконечно малая последовательность ограничена.

Доказательство.Пусть 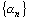– бесконечно малая последовательность, ε>0 – некоторое число, а N – номер, начиная с которого выполняется условие 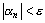. Обозначим через М наибольшее из следующих чисел 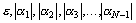. Очевидно, что 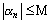для любого номера n, а это и означает, что последовательность { 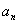} – ограничена.

Теорема 4. Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.

Доказательство. Пусть 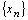– ограниченная, а 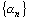– бесконечно малая последовательности. Это означает, что существует число М>0 такое, что для любого номера n выполняется 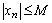, и для любого числа 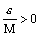существует номер N такой, что для всех номеров 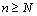выполняется 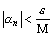. Тогда для всех номеров 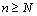и любого ε>0 выполняется 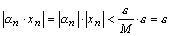, а это и означает, что последовательность 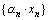– бесконечно малая.

Следствие. Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Теорема 5. Если элементы бесконечно малой последовательности 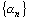равны одному и тому же числу С, то С=0.

Доказательство. Предположим, что 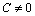. Для 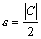существует такой номер N, что для всех номеров 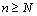выполняется 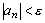. Так как 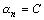, а 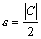, то последнее неравенство имеет вид 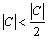, откуда 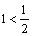. Полученное противоречие показывает, что предположение 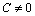неверно, следовательно, .

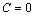Теорема 6. Если 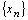– бесконечно большая последовательность то, начиная с некоторого номера n, определена последовательность 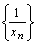, которая является бесконечно малой. Если не все элементы бесконечно малой последовательности 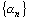равны нулю, то последовательность 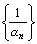бесконечно большая.

Доказательство. Пусть 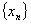– бесконечно большая последовательность. Это означает, что для любого положительного числа М можно указать такой номер N, что для всех номеров 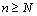выполняется 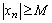. А это означает, что при 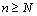все элементы 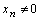, а поэтому последовательность 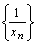имеет смысл с номера N. Пусть 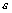- любое положительное число. Для числа 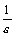можно указать номер 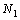такой, что для n 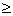N выполняется 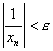. Это и означает, что 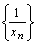– бесконечно малая. Доказательство второй части теоремы проводится аналогично.

Рассмотрим теперь лемму, которая будет использоваться при доказательстве некоторых теорем.

Лемма. Для того чтобы число а являлось пределом последовательности 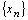, необходимо и достаточно, чтобы 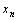имел вид 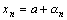, n=1,2,…, где 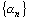есть бесконечно малая последовательность.

Доказательство. Обозначим 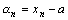. Условие 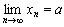по определению предела равносильно тому, что для любого числа 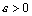существует такой номер N, что для всех номеров 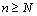выполняется неравенство 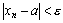, то есть 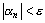, а это и равносильно тому, что .

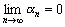Эта лемма показывает особую роль бесконечно малых последовательностей при изучении предела последовательности. Перейдем теперь непосредственно к рассмотрению простейших свойств пределов числовых последовательностей.