Распределение энергии в спектре периодического сигнала

Определим энергию отдельных гармоник

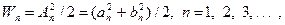(1.7)

а также энергию сигнала на одном периоде повторения:

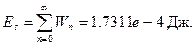
Вычисления и представление результатов проводятся по командам:

>> Wn=a.^2; E=sum(Wn); WnE= Wn/E; SWnE=cumsum(Wn)/E;

>> [n; Wn; WnE; SWnE]

Распределение энергии по спектру сигнала представлено в таблице 1.1.

Таблица 1.1 - Распределение энергии по спектру (W_n в 1e-4 В²)

n
Wn	.4752	.3800	.0950	.0038	.0038	.0050	.0005	.0005	.0009
Wn/E	.2747	.4419	.2196	.0549	.0022	.0022	.0029	.0003	.0003
SWn/E	.2747	.7166	.9362	.9911	.9933	.9955	.9984	.9987	.9989

Относительная величина энергии и нарастающее её значение в зависимости от количества гармоник представлены на рисунке 1.6 (команда plot(n,SWnE)).

Для уровня не менее 0.9Е подходит величина n₁=2, для уровня 0.99Е – n₂=3. Форма сигнала для ограниченного набора гармоник определяется по формуле (1.5) при ограниченном числе слагаемых (гармоник).

Ниже показан фрагмент расчета периодического сигнала при n₁ = 10. Вычисляются значения непрерывного сигнала и его приближённого представления конечным рядом в 256 временных точках. Графическое сравнение сигнала с его приближением, представленное на рисунке 1.7, показывает их почти полное совпадение. Однако различия между ними всё-таки заметны, хотя согласно таблице 1.1 относительная ошибка приближения заданного сигнала рядом (1.5) при n₁ = 10 меньше 0.05%.

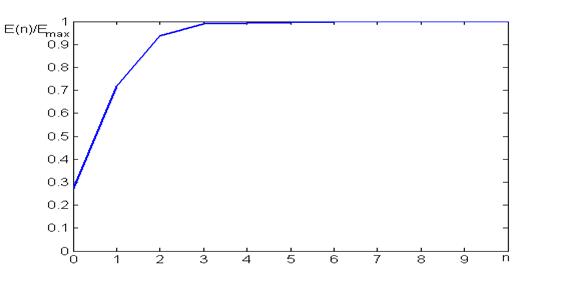
Рисунок.1.6 - Суммарная энергия начальных гармоник периодического сигнала

Um=2; Uo=1;T=1;

t = linspace(0,1,256);

s = cosinobn1(t, Um, T, Uo);

Sn = a(1);

for i=2:11; c = a(i)*cos(2*pi*n(i)*t/T); Sn = Sn+c; end

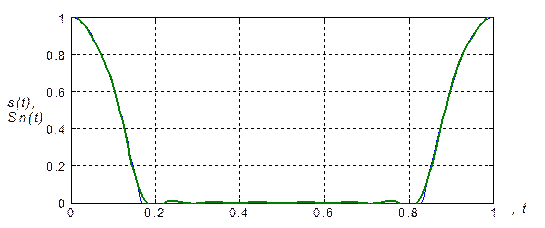
Рисунок 1.7 - Сравнение исходного периодического сигнала и его представления ограниченным (n = 10) рядом Фурье