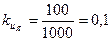Метод математического моделирования на аналоговых вычислительных машинах

Данный метод является наиболее универсальным, т.к. позволяет решать дифференциальные уравнения практически любого порядка.

При математическом моделировании используется подобие дифференциальных уравнений, которыми описываются процессы, происходящие в реальном элементе и в модели.

Чаще всего моделирование осуществляется с помощью персонального компьютера с установленной системой математических вычислений (наиболее употребительна для решения задач ТАУ система MATLAB, менее полезны системы MathCAD и Maple). Применение данных систем позволяет значительно сократить затраты труда на моделирование САУ.

Менее распространено моделирование на специальных вычислительных машинах непрерывного действия (аналоговых ЭВМ). Наиболее широко применяются электронные машины непрерывного действия типов МПТ, МН, ЭМУ, «Электрон». Рассмотрим процесс моделирования на аналоговых ЭВМ подробнее, так как он очень нагляден и непосредственно связан с использованием приведенных в данном пособии типовых схем звеньев САУ.

Все аналоговые ЭВМ построены на основе операционных усилителей постоянного тока с большим коэффициентом усиления. Например, на машине типа МН-7 к_ус=40000. Для таких усилителей при наличии обратной связи передаточная функция имеет вид:

K(p) = -Z_ос(p)/Z_вх(p). (10.18)

На схемах операционный усилитель обозначается так, как показано на рисунке 10.2:

zос

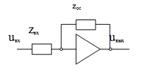
Рисунок 10.2 Схемное обозначение операционного усилителя

Так, если Z_ос = R_ос и Z_вх = R_вх, то K(p) = -R_ос/R_вх = -k.

Если Z_ос = 1/(с_осp) и Z_вх = R_вх, то 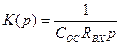, т.е. осуществляется операция интегрирования.

Процесс моделирования можно разделить на следующие этапы:

1. Определение масштабных коэффициентов.

С помощью масштабных коэффициентов устанавливается взаимнооднозначное соответствие между исходной системой уравнений и ее моделью в АВМ.

Масштабным коэффициентом физической величины x называется некоторый множитель k_x,, представляющий собой отношение машинной переменной х_м к физической х, т.е. k_x = x_м/х.

Если машинная переменная х_м представляет собой напряжение u_x, то масштабный коэффициент имеет размерность [вольт/размерность величины х].

Для повышения точности и максимального использования шкалы устройств, выполняющих отдельные операции, масштабный коэффициент для переменных выбирается из условия:

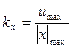(10.19)

где u_max – максимальное (линейное) допустимое значение напряжения в машине (обычно u_max = 100 В); |х|_max – максимально (по модулю) значение переменной х.

2, Переход от исходных физических уравнений к машинным уравнениям, путем замены физических величин машинным. Физические переменные умножаются на выбранные масштабные коэффициенты. Для каждого решающего элемента определяются коэффициенты передачи (при заданном коэффициенте передачи масштаб переменной соответствует выходному напряжению).

3, Составляется принципиальная схема моделирования применительно к данной АВМ. На схеме указываются номера блоков, номера входов и прочие обозначения, упрощающие работу оператора.

Рассмотрим пример составления схемы моделирования на АВМ электродвигателя постоянного тока, описываемого дифференциальным уравнением (10.20).

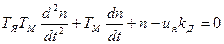(10.20)

Дано: Т_я = 0,06; Т_м = 0,037; n_н = 60 об/мин; u_н = 830 В; к_д = 0,072 (об/мин)/В; 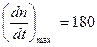(об/мин)/с.

Подставляя в уравнение (10.20) значения параметров, получим: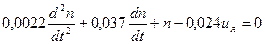

Программирование проводим в следующей последовательности.

1, По заданному физическому уравнению составляем схему моделирования (все масштабные коэффициенты считаем равными единице).

Запишем уравнение относительно старших производных:

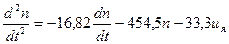(10.21)

Предполагаем, что величины 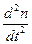уже получена, тогда на выходе интегрального усилителя У₁ будет величина 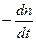, а на выходе последовательно включенного усилителя У₂ будет величина n.

Теперь обеспечим величину 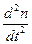на выходе первого усилителя (рисунок 10.3). Согласно уравнению (10.21) эта величина равна сумме трех слагаемых. Для формирования первого слагаемого необходимо величину 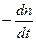умножить на масштабный коэффициент 16,82; для формирования второго слагаемого – величину n (которую необходимо получить при помощи усилителя переменного знака) умножить на коэффициент 454,5; для формирования третьего слагаемого – входную величину 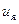необходимо умножить на коэффициент 33,3.

Если при этом операцию суммирования совместить с интегрированием, то структурная схема моделирования примет вид:

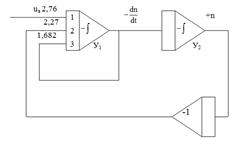
Рисунок 10.3 Схема моделирования двигателя постоянного тока на АВМ

2, Определяем масштабные коэффициенты для всех переменных:

;

;
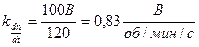
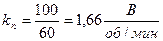