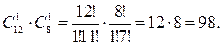П. 1.2. общие правила комбинаторики

Рассмотрим k множеств М₁, М₂, М₃,...,М_k содержащих по m₁, m₂, m₃,...,m_k элементов соответственно. Выбирается по одному элементу из каждого множества и составляется еще одно множество. Число способов, которыми можно выбрать по одному элементу из каждого множества, равно произведению m₁, m₂, m₃,...,m_k. В этом и состоит основной принцип комбинаторики.

В задачах теории вероятностей часто рассматриваются различные соединения (комбинации) из множества n элементов по k элементов (k≤n). Будем рассматривать такие соединения, в которые каждый элемент данного множества может входить не более одного раза, т. е. соединения без повторений.

Рассмотрим три вида соединений: 1) размещения, 2) перестановки, 3) сочетания.

Определение. Размещениями из n элементов по k элементов называются подмножества k элементов, отличающиеся одно от другого или самими элементами или их порядком. Число размещений обозначается .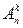

Теорема. Число размещений из n элементов по k элементов

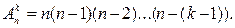(1.2.1)

Пример. Определить, сколько трехзначных чисел можно составить из множества цифр 1, 2, 3, 4, 5 без повторений.

Решение. Имеем n = 5, k=3; 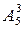=5∙4∙3=60.

Здесь полагали, что 0<k≤n. При k =0 ,по определению, 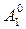=1

Определение. Перестановками из данных n элементов называются множества из n элементов, различающихся только порядком.

Перестановки - это частный случай размещений. Число всех перестановок обозначают символом Р_n. Число Р_n найти несложно. Для этого в формуле (11.2.1) необходимо положить k = n. Имеем

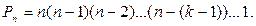
Определение. Произведение n первых натуральных чисел обозначается символом n! (читается эн-факториал). Поэтому

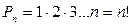(1.2.2)

По определению принимается Р₀ = О! = 1.

Пример. К кассе за получением (для уплаты) денег подошли одновременно 4 человека. Сколькими способами они могут выстроиться в очередь.

Решение. Очередь состоит из четырех различных лиц, поэтому в каждом способе составления очереди учитывается порядок их расположения. Таким образом, имеют место перестановки из четырех человек, их число равно

Р₄=1∙2∙3∙4=24.

Определение. Сочетаниями, содержащими k элементов, выбранных из n элементов заданного множества, называются всевозможные множества, различающиеся хотя бы одним элементом. Число сочетаний из n элементов по k элементов обозначают .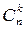

Теорема. Число сочетаний из n элементов по k элементов определяется формулой

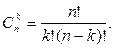(1.2.3)

Пример 1. Имеется 6 штаммов бактерий. Для определения скорости их роста необходимо выбрать 3 штамма. Сколькими способами можно это сделать?

Решение. Способы отбора считаются различными, если каждая отобранная группа штаммов различается хотя бы одним элементом. Это число

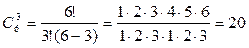
Таким образом, имеется 20 способов.

Пример 2. В ящике 20 шаров, среди которых 12 белых, остальные - голубые. Отбирается наугад 2 шара. Сколькими способами можно отобрать: а) два белых шара; б) два голубых; в) один белый, другой голубой.

Решение. Число способов, которыми можно отобрать два белых шара из 12, не зависит от порядка отбора и равно числу множеств из 12 и 2, различающихся только составом. Следовательно,

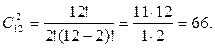
Число способов, которыми можно отобрать 2 голубых шара из 8 ровно

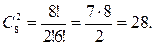
Число способов, которыми можно отобрать один белый, другой голубой шар, согласно основному принципу комбинаторики равно 12∙8=98, или