Аксіоми додавання і множення
Для будь-якої пари 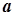 та
та 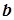 дійсних чисел однозначно виражене число
дійсних чисел однозначно виражене число 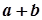 , яке називається їх сумою.
, яке називається їх сумою.
Для будь-якої пари 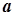 і
і 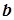 дійсних чисел однозначно виражене число
дійсних чисел однозначно виражене число 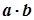 , яке називається їх добутком.
, яке називається їх добутком.
Для будь-яких дійсних чисел a, b, c виконуються наступні аксіоми:
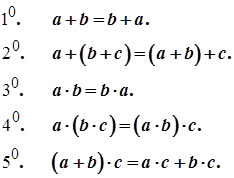
 Існує єдине число 0, таке, що
Існує єдине число 0, таке, що 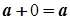 для будь-якого числа
для будь-якого числа 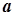 .
.
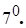 Для будь-якого числа
Для будь-якого числа 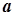 існує таке число
існує таке число 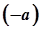 , що
, що 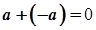 (число
(число 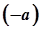 називається протилежним числу
називається протилежним числу 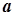 ).
).
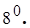 Існує єдине число 1, таке, що
Існує єдине число 1, таке, що 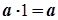 для будь-якого числа
для будь-якого числа 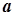 .
.
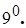 Для будь-якого числа
Для будь-якого числа 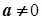 існує таке число
існує таке число 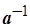 , що
, що 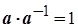 ; число
; число 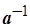 позначається також символом
позначається також символом 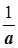 і називається оберненим до
і називається оберненим до 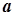 .
.
Аксіоми порівняння дійсних чисел
Для будь-яких дійсних чисел a, b установлене одне із співвідношень: 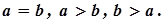
Відношення "=" має властивість: якщо 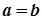 і
і 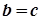 , то
, то 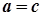 .
.
Для будь-яких дійсних чисел a, b, c виконуються наступні аксіоми:
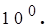 Якщо
Якщо 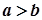 і
і 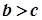 , то
, то 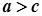 .
.
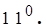 Якщо
Якщо 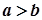 , то
, то 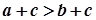 .
.
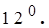 Якщо
Якщо 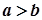 і
і 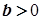 , то
, то 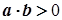 .
.
Зауваження. Замість 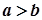 пишуть
пишуть 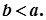
Аксіома неперервності дійсних чисел
 Нехай
Нехай 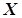 і
і 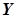 - дві множини, які складаються із дійсних чисел. Тоді, якщо
- дві множини, які складаються із дійсних чисел. Тоді, якщо 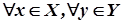 , виконується нерівність
, виконується нерівність 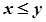 , то існує принаймні одне дійсне число
, то існує принаймні одне дійсне число 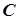 , для якого виконується нерівність
, для якого виконується нерівність 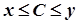 .
.
Зауваження. У множині лише раціональних чисел аксіома неперервності не виконується. Дійсно, нехай 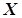 складається із множини раціональних чисел, таких, що
складається із множини раціональних чисел, таких, що 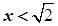 , а
, а 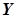 − із множини раціональних чисел
− із множини раціональних чисел 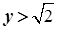 . Тоді
. Тоді 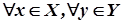 виконується нерівність
виконується нерівність 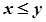 . Проте не існує раціонального числа
. Проте не існує раціонального числа 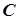 , такого, щоб
, такого, щоб 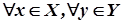 виконувалася б нерівність
виконувалася б нерівність 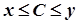 . Таким числом могло бути лише число
. Таким числом могло бути лише число 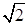 , а воно, як відомо, ірраціональне.
, а воно, як відомо, ірраціональне.
Деякі властивості дійсних чисел
Наведемо деякі властивості дійсних чисел.
1. Число 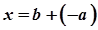 є розв'язком рівняння
є розв'язком рівняння 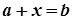 .
.
Доведення. Підставимо в дане рівняння замість 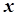 його значення:
його значення:
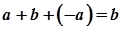 .
.
Згідно з 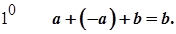
Згідно з 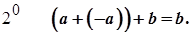
Згідно з 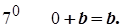
Згідно з 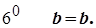
Зауваження. Число 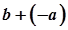 називається різницею чисел
називається різницею чисел 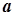 та
та 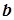 і позначається
і позначається 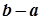 . Зазначимо, що за умови
. Зазначимо, що за умови 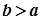 різниця
різниця 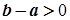 . Дійсно, якщо
. Дійсно, якщо 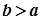 , то за
, то за 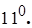 Одержуємо
Одержуємо 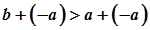 , далі за
, далі за 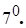 Маємо
Маємо 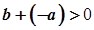 , тобто
, тобто 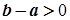 .
.
2. Число 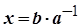 є розв'язком рівняння
є розв'язком рівняння 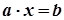 , якщо
, якщо 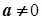 .
.
Доведення. Підставимо в дане рівняння значення 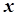 :
:
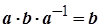 .
.
Згідно з 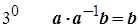 .
.
Згідно з 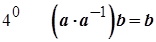 .
.
Згідно з 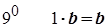 .
.
Згідно з 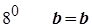 .
.
Зауваження. Число 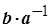 називається часткою чисел
називається часткою чисел 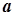 й
й 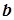 і позначається
і позначається 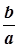 або
або 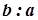 .
.
3. Якщо 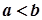 , то
, то 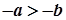 .
.
Дійсно, оскільки 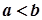 , то
, то 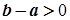 . Отже, за
. Отже, за 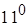
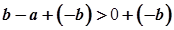 , звідки одержуємо
, звідки одержуємо 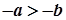 .
.
Зокрема, якщо 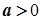 , то
, то 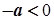 , а якщо
, а якщо 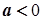 , то
, то 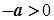 .
.
Дійсно, згідно з 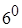
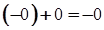 , далі за
, далі за 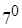
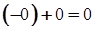 . Отже,
. Отже,
0= − 0.
4. Якщо 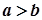 і
і 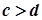 , то
, то 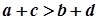 .
.
Дійсно, якщо 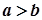 і
і 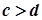 , то за
, то за 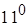
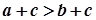 ,
, 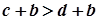 . Далі згідно з
. Далі згідно з 
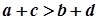 .
.
5. Якщо 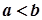 та
та 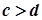 , то
, то 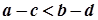 .
.
Дійсно, якщо 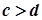 , то згідно з
, то згідно з 
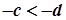 і за 4 одержуємо:
і за 4 одержуємо: 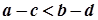 .
.
6. 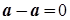 .
.
Це випливає з того, що 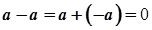 .
.
7. 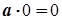 .
.
Справді, 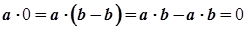 .
.
8. 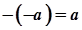 .
.
Дана рівність доводиться так: 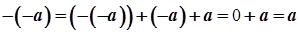 .
.
9. 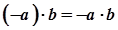 .
.
Доведення: 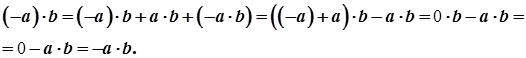
Зокрема, 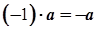 .
.
10. Якщо 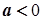 і
і 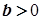 , то
, то 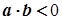 .
.
Дійсно, оскільки 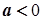 , то
, то 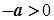 , а тому
, а тому 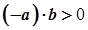 (згідно з
(згідно з 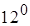 ). Отже,
). Отже, 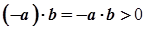 , а звідси
, а звідси 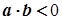 .
.
11. Якщо 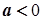 та
та 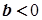 , то
, то 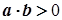 .
.
Справді, оскільки 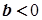 , то
, то 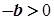 , а тому
, а тому 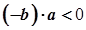 (згідно з
(згідно з 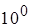 ). Отже,
). Отже, 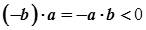 , а звідси маємо
, а звідси маємо 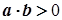 .
.
12. Якщо 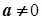 , то
, то 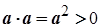 .
.
Це випливає з 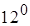 і 11.
і 11.
За властивістю 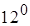 маємо:
маємо: 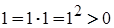 , тобто
, тобто 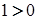 .
.
Надалі будемо використовувати й інші властивості дійсних чисел, не спиняючись на їх формальному доведенні.
