Сравнение бесконечно малых. Эквивалентные бесконечно малые
1) Пусть 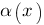 и
и 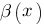 — бесконечно малые при
— бесконечно малые при 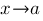 .
.
1. Если 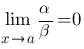 , то говорят, что
, то говорят, что 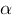 является бесконечно малой высшего порядка по сравнению с
является бесконечно малой высшего порядка по сравнению с 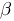 . В этом случае пишут
. В этом случае пишут 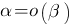 .
.
2. Если 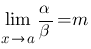 , где
, где 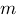 —число, отличное от нуля, то говорят, что
—число, отличное от нуля, то говорят, что 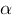 и
и 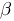 — бесконечно малые одного и того же порядка. В часности, если
— бесконечно малые одного и того же порядка. В часности, если 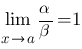 , то бесконечно малые
, то бесконечно малые 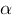 и
и 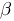 называются эквивалентными. Запись
называются эквивалентными. Запись 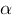 ~
~ 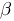 означает, что
означает, что 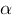 и
и 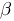 —эквивалентные бесконечно малые.
—эквивалентные бесконечно малые.
Если 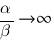 , то это означает, что
, то это означает, что 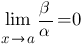 . Таким образом,
. Таким образом, 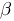 является бесконечно малой высшего порядка по сравнению с
является бесконечно малой высшего порядка по сравнению с 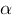 , т. е.
, т. е. 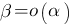
3. Если 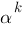 и
и 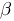 —бесконечно малые одного и того же порядка, причем
—бесконечно малые одного и того же порядка, причем 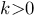 , то говорят, что бесконечно малая
, то говорят, что бесконечно малая 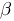 имеет порядок
имеет порядок 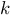 по сравнению с
по сравнению с 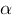 .
.
Отметим некоторые свойства бесконечно малых величин:
1o. Произведение двух бесконечно малых есть бесконечно малая высшего порядка по сравнению с сомножителями, т. е. если 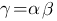 , то
, то 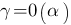 и
и 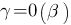 .
.
2o. Бесконечно малые 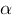 и
и 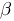 эквивалентны тогда и только тогда, когда их разность
эквивалентны тогда и только тогда, когда их разность 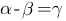 является бесконечно малой высшего порядка по сравнению с
является бесконечно малой высшего порядка по сравнению с 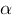 и
и 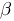 , т. е. если
, т. е. если 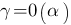 ,
, 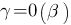 .
.
3o. Если отношение двух бесконечно малых имеет предел, то этот предел не изменится при замене каждой из бесконечно малых эквивалентной ей бесконечно малой, т.е. если
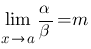 ,
, 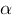 ~
~ 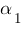 ,
, 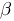 ~
~ 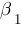 , то
, то 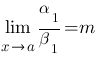 .
.
2) Б.м. функции 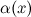 и
и 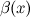 называются эквивалентными или равносильными б.м. одного порядка при
называются эквивалентными или равносильными б.м. одного порядка при 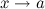 , если
, если 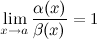
Обозначают: 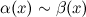 при
при 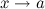 .
.
Очень удобно пользоваться заменой эквивалентных бесконечно малых при нахождении пределов. Замена производится на основе таблицы.
Таблица эквивалентных бесконечно малых.
Пусть 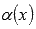 - бесконечно малая при
- бесконечно малая при 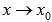 .
.

