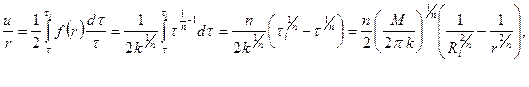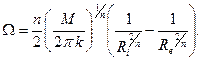Вращательное движение жидкости в кольцевом зазоре

Рассмотрим установившееся ламинарное вращательное движение вязкой жидкости в кольцевом зазоре между двумя соосными цилиндрами бесконечной высоты. При этом жидкость движется по круговым траекториям, плоскости которых перпендикулярны оси цилиндров. Схема движения имеет вид, представленный на рисунке 3.4.

Выделим в потоке элемент радиуса r и толщиной dr (рис 3.5). Если бы жидкость вращалась как твердое тело с угловой скоростью 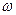, то за время dt тока А перешла бы в положение 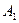. В действительности за счет деформации жидкости эта точка переходит в положение 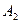и угол скашивания 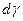равен:

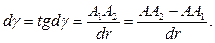(3.55)

Очевидно, что путь 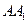равен:

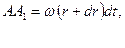
а

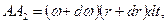
где 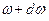- угловая скорость частиц, лежащих на окружности радиуса .

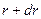Подставив полученные отношения в формулу (3.55), получим

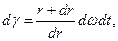
откуда после перехода к пределу при 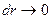имеем

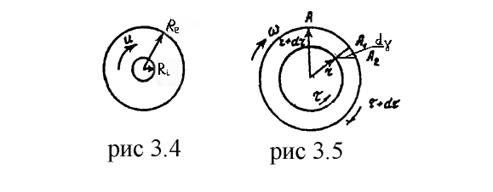
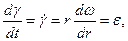(3.56)

то есть формулу для определения скорости сдвига при вращательном течении жидкости в кольцевом зазоре.

Рассмотрим выделенный в потоке элемент радиуса r, толщиной dr и высотой h. Сила, приложенная к цилиндрической поверхности радиуса r равна 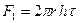, а к поверхности радиус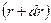а равна .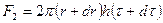

Так как выделенный элемент вращается с постоянной по времени угловой скоростью 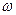, то сумма моментов сил, приложенных к этому элементу, равна нулю, то есть

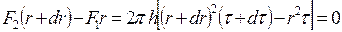(3.57)

После элементарных преобразований и переходя к пределу при dr 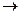0, из (3.57) получим

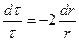(3.58)

или, после интегрирования

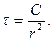(3.59)

Для определения константы интегрирования С обозначим момент сил трения на внутреннем цилиндре радиуса и единичной длины через М. Тогда

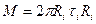(3.60)

где 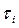- напряжение трения на радиусе 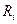.Из формулы (3.59) следует, что

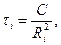
а из формулы (3.60)

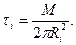
Приравняв эти выражения, получим

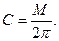(3.61)

Подставив выражение (3.61) в формулу (3.59), получим окончательно

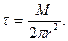(3.62)

Подставив соотношения (3.56) и (3.62) в соотношение 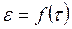, получим

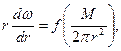(3.63)

то есть дифференциальное уравнение вращательного движения жидкости в кольцевом зазоре.

Для интегрирования этого уравнения примем, что внутренний цилиндр покоится, а внешний вращается с угловой скоростью 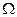. Тогда скорость течения на поверхности внутреннего цилиндра радиус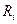а равна

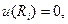(3.64)

а на поверхности внешнего цилиндра радиуса -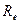

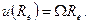(3.65)

Так как угловая скорость 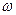равна

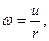
то из уравнения (3.63) имеем

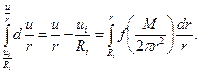(3.66)

Формула (3.66) может быть представлена в виде

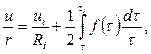(3.67)

где

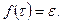(3.68)

Полученное выражение дает закон распределения скорости течения в кольцевом зазоре между двумя соосными цилиндрами. Положим в этом отношении r=R_е и, соответственно, 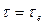, найдём

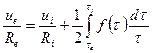
или, использовав формулы (3.64) и (3.65)

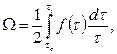(3.69)

то есть получим формулу для определения угловой скорости вращения внешнего цилиндра.

Рассмотрим теперь течение вязкопластичной жидкости (жидкости Бингама – Шведова) в кольцевом зазоре. Так как 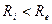, то в соответствии с формулой (3.62) всегда 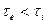. Поэтому до тех пор пока 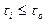, то есть 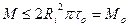, сдвига не происходит, то есть 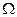=0, и жидкость между цилиндрами неподвижна.

При М > М₀ имеем 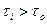. Пусть 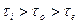. Так как вдоль радиуса M=const, то из формулы (3.62) следует, что

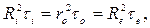
где - 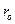- радиус на котором 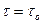. Тогда, очевидно, при 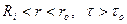, а при .

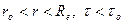Следовательно, в интервале 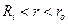будет происходить сдвиговое течение , а при 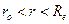жидкость будет вести себя как твердое тело, то есть вращаться с постоянной угловой скоростью.

Из формул (3.67 – 3.69) получим с учетом соотношения (3.62) при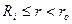

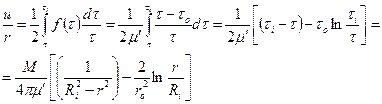
при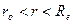

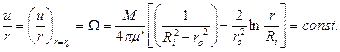
В соответствии с формулой (3.62)

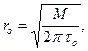
то есть с ростом момента М величина 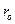, и, следовательно, область, охваченная сдвиговым течением, также возрастает.

При 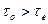сдвиговым течением охвачена вся область и в соответствии с формулой (3.69)

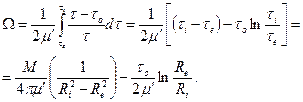
Если в кольцевом зазоре находится степенная жидкость, то полагая

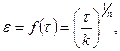
из формул (3.67) и (3.68) получим соотношения