Охлаждение (нагревание) неограниченной пластины

Рассмотрим расчетные зависимости, полученные аналитическим методом [1,2,3], на примере охлаждения плоской стенки, размеры которой по длине и ширине настолько велики, что теплообменом с торцов можно пренебречь. При одинаковых условиях теплообмена на обеих поверхностях температурное поле будет одномерным и симметричным относительно середины стенки. Поэтому на рис. 4.1 ее толщина обозначена через 2d.

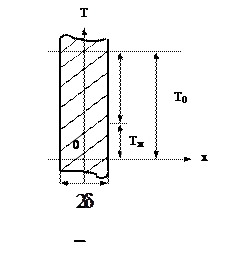
Будем полагать, что температура окружающей пластину жидкости Тж=const и коэффициент теплоотдачи a= const. С учетом принятых ранее обозначений для избыточных температур 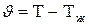дифференциальное уравнение (3.2) будет иметь вид

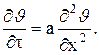(4.1)

Рис. 4.1

Начальные условия:

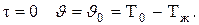при (4.2)

При этом граничные условия в середине и на поверхности пластины соответственно можно записать так:

при х=0 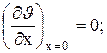(4.3)

при х=d 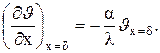(4.4)

Решение этой задачи позволяет выразить безразмерную температуру в виде ряда

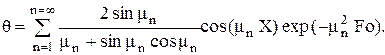(4.5)

Здесь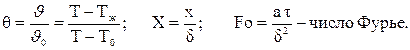

Числа m_n определяются из трансцендентного уравнения

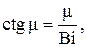(4.6)

где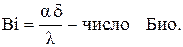

Так как m₁, m₂,….., m_n представляет собой ряд возрастающих чисел, то чем больше m, тем меньше роль последующего члена ряда в (4.5) по сравнению с предыдущим. Кроме того, чем больше число Fo, тем быстрее будут убывать члены знакопеременного (из-за cos m_n X) ряда (4.5) с увеличением номера n. Исследования показали, что уже при Fo 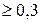ряд (4.5) становится настолько быстросходящимся, что распределение температуры достаточно точно, с ошибкой не более 1 %, описывается первым членом ряда (4.5)

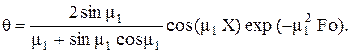(4.7)

Как видно из (4.7), при фиксированной безразмерной координате Х натуральный логарифм безразмерной температуры q линейно зависит от безразмерного времени Fo. Для Х=0 и Х=1 решение (4.7) в [1] представлено в виде номограмм для различных значений чисел Био, так как m₁ зависит в соответствии с (4.6) только от числа Био. Эти номограммы можно использовать в практических расчетах.

При Bi ®¥ (практически при Bi >100) из (4.6) имеем ctg m=0 и m_{n 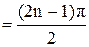,} где n=1, 2, …… В этом случае температура поверхности пластины сразу при Fo>0 становится равной температуре окружающей среды, а безразмерная температура q при Х=1 q=0. Иначе говоря, процесс отвода теплоты с поверхности тела происходит существенно интенсивнее, чем выравнивание температуры в теле. В этом случае процесс охлаждения (нагревания) определяется размерами тела и его физическими свойствами.

При Bi ®0 (практически при Bi < 0,1) ctg m=¥ и m_n =(n-1)p. В этом случае все члены ряда (4.5), кроме первого, равны нулю. Но при m₁ ®0

.

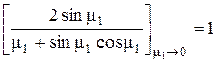С другой стороны, при m₁ ®0 .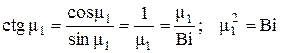

Учитывая это, уравнение (4.5) можно переписать в виде

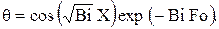(4.8)

При малых числах Bi значение 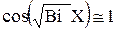и температура на поверхности пластины мало отличается от температуры в центре. Это указывает на то, что температура по толщине пластины практически распределяется равномерно. Иначе говоря, процесс выравнивания температуры в теле происходит существенно интенсивнее, чем отвод теплоты с поверхности тела, и задача охлаждения (нагревания) становится внешней.

Количество отданной (полученной) стенкой теплоты на любой момент времени t₁ можно определить из следующих соображений. Количество отданной (полученной) стенкой теплоты с обеих ее поверхностей за время от t=0 до t=¥ должно равняться (в изобарном процессе) изменению энтальпии пластины за период ее полного охлаждения (нагревания)

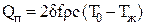, (4.9)

где с – удельная теплоемкость;

f – площадь боковой поверхности;

r – плотность.

Тогда за любой промежуток времени от t=0 до t=t_1., или, что то же, от Fo=0 до Fo= Fo₁, энтальпия пластины изменится на

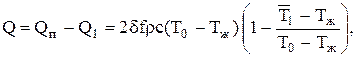
или

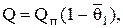(4.10)

где 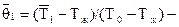средняя безразмерная температура по толщине пластины в момент времени t₁.

Из соотношений (4.9) и (4.10) следует, что расчет количества теплоты, отданного (полученного) пластиной, сводится к нахождению средней безраз-мерной температуры в интересующий нас момент времени. Средняя безраз-мерная температура для слоя пластины от ее центра до плоскости Х равна

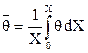
в соответствии с теоремой о среднем.

Если в это выражение подставим под знак интеграла значение q из уравнения (4.5) и проинтегрируем в пределах от нуля до единицы, то получим

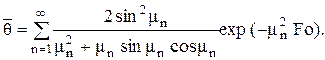(4.11)

Подставив в уравнение (4.10) вычисленное по формуле (4.11) значение средней температуры пластины для интересующего нас момента времени Fo, получим количество теплоты, отданное пластиной в окружающую среду за этот промежуток времени.

Регулярный режим

Как показано выше, начиная с некоторого момента времени t>t₁ охлаждения пластины, начальные условия начинают играть второстепенную роль. Процесс полностью определяется только условиями охлаждения на границе пластины и среды, физическими свойствами материала тела и его геометрической формой и размерами. Математически это означает, что температурное поле в пластине описывается первым членом ряда (4.5)

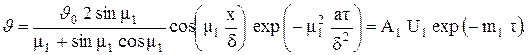(4.12)

В этом уравнении А₁-постоянный коэффициент, не зависящий ни от координат, ни от времени, так как m₁ определяется из соотношения (4.6). Множитель U_n является функцией только координаты х. Для тел других геометрических форм температурное поле в стадии регулярного режима также будет описываться уравнением вида (4.12). Специфика геометрической формы учитывается различным видом множителей А₁ и U₁. Логарифмируя последнее уравнение и опуская индексы, получим

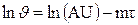. (4.13)

После дифференцирования обеих частей уравнения (4.13) имеем

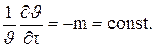(4.14)

Величина m называется темпом охлаждения. При наступлении регулярного режима темп охлаждения не зависит ни от координат, ни от времени и является величиной постоянной для любой точки тела. Если экспериментально определить изменение избыточной температуры J во времени t и построить зависимость в полулогарифмических координатах, то темп охлаждения в стадии регулярного режима найдется как

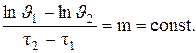(4.15)

Зависимость темпа охлаждения от физических свойств материала тела, его геометрической формы и размеров, а также условий теплообмена на поверхности тела можно найти из теплового баланса. При отводе от тела объемом V тепла dQ изменение энтальпии тела составит

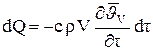, (4.16)

где 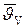– средняя по объему избыточная температура.

За тот же промежуток времени эта теплота должна быть отведена с поверхности тела в окружающую среду за счет теплоотдачи

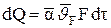. (4.17)

Приравнивая выражения (4.16) и (4.17), получим

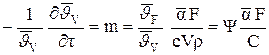. (4.18)

Из этого уравнения следует, что относительная скорость охлаждения или темп охлаждения тела при конечном значении коэффициента теплоотдачи прямо пропорциональна коэффициенту теплоотдачи, поверхности тела и обратно пропорциональна его теплоемкости (первая теорема Кондратьева [1]). В этом уравнении множитель 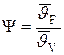называется коэффициентом неравномерности распределения температуры в теле. При Bi®0 (практически при Bi<0,1) y=1. При Bi®¥ (практически при Bi>100) y=0.

При Bi®¥, или, что то же, a®¥, темп охлаждения становится прямо пропорциональным коэффициенту температуропроводности материала тела (вторая теорема Кондратьева [1]).

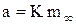. (4.19)

Коэффициент пропорциональности К зависит от геометрической формы и размеров тела. Докажем это на примере охлаждения пластины. Напомним, что из соотношения (4.12) следует

,

при Bi®¥ имеем ctg m®0, а m стремится к своему предельному значению p/2. С учетом этого коэффициент пропорциональности для пластины равен

;

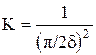для шара

;

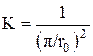для параллелепипеда

;

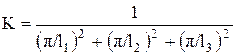для цилиндра конечной длины

.

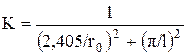На основе теории регулярного режима разработаны различные экспериментальные методы определения теплофизических свойств разных материалов. При определении этих свойств поступают следующим образом. Для определения коэффициента температуропроводности используют a-калориметр, имеющий форму цилиндра или шара. Создают условия охлаждения, близкие к a®¥, измеряют изменение избыточной температуры во времени и строят зависимость в полулогарифмических координатах. По соотношению (4.15) определяют темп охлаждения, а по формуле (4.19) рассчитывают коэффициент температуропроводности.

Конвективный теплообмен

Основные понятия и определения

Понятие конвективного теплообмена охватывает процесс теплообмена при движении жидкости. При этом перенос теплоты осуществляется одновременно, как это показано в главе 1, конвекцией и теплопроводностью. В любой точке потока жидкости плотность теплового потока определяется соотношением (2.3)

.

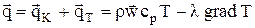Поэтому, если определить плотность теплового потока в точках на границе обтекаемого жидкостью твердого тела и проинтегрировать по всей поверхности, то можно рассчитать поток тепла, подводимый (или отводимый) к этому телу. Если проинтегрировать полученное соотношение для потока тепла по интересующему нас промежутку времени, то можно определить количество тепла, подведенного (или отведенного) к телу за этот промежуток времени. Однако, как это видно из соотношения для плотности теплового потока, для этого необходимо знание полей скоростей и температур в движущейся жидкости. Для определения этих полей можно использовать дифференциальные уравнения сохранения массы (уравнение неразрывности), сохранения энергии (уравнение энергии) и уравнение движения в проекциях на координатные оси, которые были выведены в главе 2. Система этих пяти уравнений при соответствующих краевых условиях для конкретной задачи конвективного теплообмена, в принципе, казалось бы, позволяет решить задачу. Т.е. определить поле температур T=T(x,y,z,t), поля проекций скоростей на оси координат w_x=w_x(x,y,z,t), w_y=w_y(x,y,z,t), w_z=w_z(x,y,z,t) и поле давлений p=p(x,y,z,t). Попытки аналитического решения системы уравнений, даже для ламинарного течения жидкости, наталкиваются на серьезные математические трудности. При ламинарном течении жидкости частицы жидкости движутся без перемешивания, слоисто. Поперек потока ламинарно-текущей жидкости тепло передается только теплопроводностью. Турбулентное течение жидкости представляет собой хаотическое движение разных по размерам частиц жидкости с их перемешиванием. Любая физическая величина (температура, скорость, давление и т.д.), измеренная в фиксированной точке турбулентного потока жидкости, показывает хаотические пульсации около некоторого среднего во времени значения. Мгновенные значения скорости w, температуры T, давления р можно представить в виде суммы средних во времени значений и пульсационных:

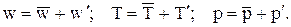
Если подставить эти мгновенные значения скорости w, температуры T, давления р в выведенные в главе 2 дифференциальные уравнения конвективного теплообмена, то последние существенно усложняются. Физический анализ процессов конвективного теплообмена показывает, что в ряде случаев дифференциальные уравнения могут быть упрощены без внесения существенных погрешностей. Например, математическая формулировка задачи может быть упрощена при использовании понятия пограничного слоя.