Дәріс. Көп айнымалы функциялардың туындылары мен дифференциалдары

Дербес өсімшелер мен дербес туынды.Бір айнымалы функциямен салыстырғанда көп айнымалылы функцияның өсімшелерінің түрлері көп болады. Бұл жағдайда 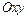жазықтығындағы қозғалыс 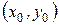нүктесінен әртүрлі бағыттарға қарай жүретініне байланысты.

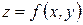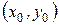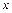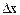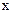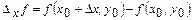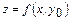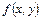Анықтама. функциясының нүктесіндегі бойынша өсімшесі -ке сәйкес бойынша дербес өсімшесі деп айтамыз. Бұл өсімше, бір айнымалы функцияның тұрақты болғанда функциясының өсімшесі болады. Сол сияқты 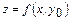функциясының 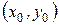нүктесіндегі 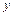- бойынша өсімшесі 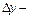ке сәйкес 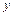бойынша дербес өсімшесі деп мына айырманы айтамыз: 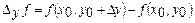. Бұл өсімше 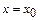тұрақты мәнінде есептелінеді.

7-мысал. 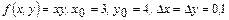болсын. 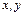бойынша функцияның дербес өсімшелерін табайық: ;

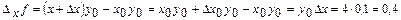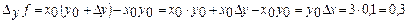; Бұл мысалда аргументтердің бірдей өсімшелерінде 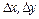, дербес өсімшелер әртүрлі. Бұл тікбұрыштың қабырғалары 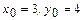болатын, 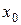-ді 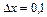ге өсіргенде ауданының 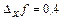-ке, ал 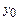қабырғасын 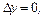1-ге өсіргенде ауданының 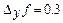- ке өсетінін білдіреді.

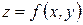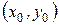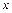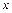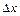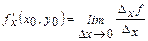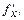
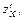
Анықтама. функциясының нүктесіндегі дербес туындысы деп осы функцияның бойынша дербес өсімшесінің, осы нүктедегі, аргументінің өсімшесі - ке қатынасын айтады: . Мұндай дербес туындылар 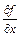, 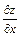символдарымен белгіленеді. Соңғы жағдайда 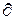-әрпі «дербес» сөзін береді. Осы 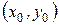нүктесіндегі 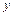бойынша дербес туынды мына 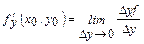. шеккпен анықталады.

Бұл дербес туындының басқа белгіленулері: 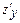, 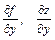. Функциялардың дербес туындысы бір айнымалы функцияның туындыларын табу ережелері бойынша табылады, дифференциалданатын айнымалыдан басқа айнымалалар тұрақты деп есептелінеді. 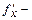табу кезінде 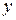турақты деп есептеледі, ал 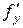тапқанда 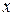- тұрақты деп есептеледі.

8-мысал. 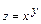функциясының дербес туындыларды табайық: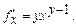

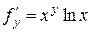
9-мысал. 3 айнымалы функцияның дербес туындыларын табайық: .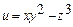

.

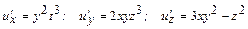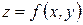функциясының дербес туындылары бір айнымалыны уақтша тұрақты деп белгілеп алғандағы функцияның жылдамдығын көрсетеді.

Анықтама. 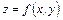функциясының дербес туындылары бар болса, онда оның дербес дифференциалдары деп 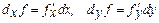өрнектері аталады, мұндағы .

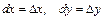Екі айнымалы функцияның дербес дифференциалдары осы екі айнымалының біреуін тұрақты деп белгілеп алғандағы бір айнымалы функцияның дифференциалдары болып табылады.

Толық өсімше мен толық дифференциал.Функцияның толық өсімшесінің дербес өсімшелерден айырмашылығы - барлық айнымалылары өзгеріп отыратындығында.

Анықтама 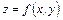функциясының 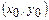нүктесіндегі аргументтердің 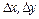өсімшелеріне сәйкес толық өсімшесі деп мына айырманы айтады:

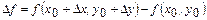. (1)

10-мысал. 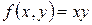, , 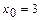, 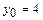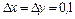(алдыңғы мысалды қара). 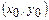нүктесіндегі толық өсімшені табайық:

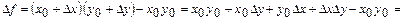
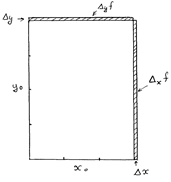
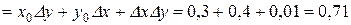. Бұл өсімше табандары 3,4 болатын тік төртбұрыштың әр қабырғасын 0,1 - ге өсіргендегі тік төртбұрыштың ауданының өсімшесіне тең, суретте толық 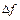өсімшесі екі штрихтелген аудандарына және оған қабырғасы 0,1 - ге тең квадраттың ауданы қосылған.

Анықтама.Егер 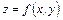функциясының 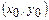нүктесіндегі толық өсімшесін

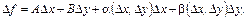мұндағы 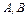- тұрақты, 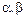- шексіз аз 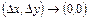жазуға болатын болса, онда 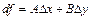функцияның 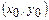нүктесіндегі толық дифференциалы деп аталады. Толық дифференциалды функция өсімшесін негізгі бөлігі деп атайды. Белгілі бір нүктеде толық дифференциалы бар функция осы нүктеде дифференциалданатын функция деп аталды.

Теорема 1. 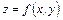функциясы және оның дербес 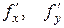туындыларды 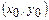нүктесінің кейбір аймағында үзіліссіз болсын. Онда 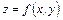функциясы 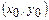нүктесінде дифференциалданады және оның толық дифференциалы дербес дифференциалдардың қосндысына тең: 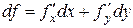(2)

Дәлелдеуі . Толық өсімше 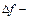ті былай түрлендірейік:

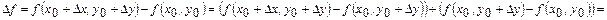
(әр айырмаға Лагранж теоремасын қолданайық) = 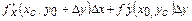, мұндағы .

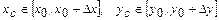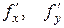үзіліссіздіктерінен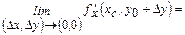 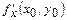және 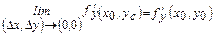шығады. Сондықтан бұл дербес туындыларды мына түрде жазуға болады: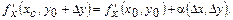

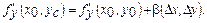
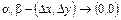- шексіз аз шамалар. Сондықтан

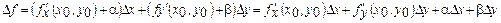, анықтама бойынша 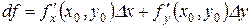болады. Сонымен теорема дәлелденді.

11-мысал. 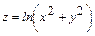функциясының толық дифференциалын табыңдар. Бұл функцияның дербес туындыларын табайық: 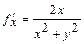; ; 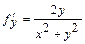Бұларды (2) - ге қойсақ, онда мынаны аламыз: 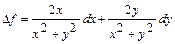. Егер (1) формулдағы толық өсімшені толық дифференциалмен ауыстырсақ, онда функцияның жуықтап табу формуласын аламыз: 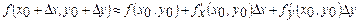(3)

12-мысал. 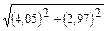санды жуықтап есептейік. Ол үшін 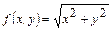функциясының 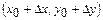нүктедегі, мұнда 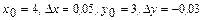, мәнін жуықтап есептейік: 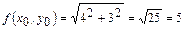; ; 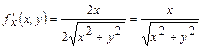; ; 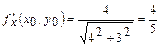; 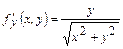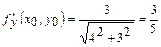Бул мәндерді (3) – ке қойып аламыз; .

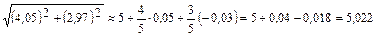Ескерту. 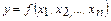көп айнымалы функциясының толық дифференциалы мына формуламен есептелінеді: .

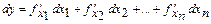13-мысал. 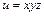3 айнымалы функцияның толық дифференциалын табайық: 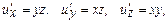онда .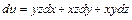

Әдебиеттер: 9 нег.[237-243], 11 нег. [308-313].

Бақылау сұрақтар:

1. Бірінші ретті дербес туынды.

2. Екі айнымалы функцияның дербес туындыларының геометриялық мағынасы.

3. Жоғары ретті дербес туындылар ұғымы.

4. Функцияның дифференциалдануы.

5. Жоғарғы ретті дифференциалдар.