Система нелінійних рівнянь

На відміну від СЛАР для систем нелінійних рівнянь (СНР) не існує прямих методів розв’язку, а тому їх розв’язують лише ітераційними способами. В загальній формі СНР записується так:

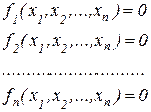, (6.3)

або в векторній формі 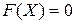, де Х – вектор невідомих, 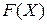– вектор-функція.

Для одержання ітераційної формули створення процесу прямої ітерації приведемо систему (6.3) до вигляду:

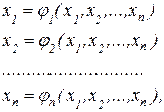
що в векторній формі записують .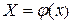

Задавши початкове значення вектора невідомих 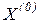, одержуємо ітераційний процес: 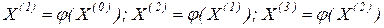і т.д., допоки різниця норм векторів Х на сусідніх ітераціях не стануть менше наперед заданого малого числа e:

.

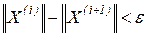Недоліком таких процесів є те, що початкове значення 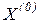потрібно вибирати лише в зоні збіжності поблизу точки розв’язку. Цю зону визначають із фізичних властивостей процесів чи об’єктів, режим роботи яких описується даною системою нелінійних рівнянь. В двовимірному просторі зону збіжності можна визначати графічно.

Наступним обмеженням застосування метода прямої ітерації є те, що для створення збіжного ітераційного процесу перетворення 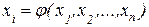потрібно здійснити таким чином, щоб

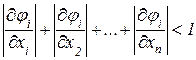
Наведемо приклад розв’язку СНР для двох невідомих:

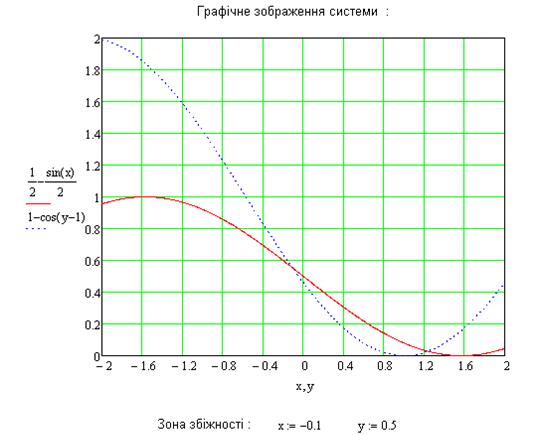
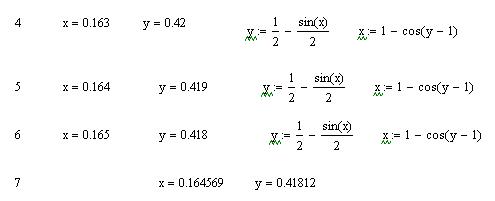
Найбільшого поширення в інженерній практиці при розв’язуванні СНР набув метод Ньютона, який має ряд переваг перед іншими ітераційними методами. В першу чергу – це його значна швидкість збіжності. Для побудови ітераційного процесу за цим методом вектор-функцію 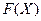розкладемо в n-вимірному просторі в ряд Тейлора:

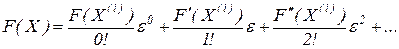
Згідно (6.3) 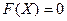. Далі в цьому ряду

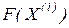– вектор-функція, розміщена в зоні збіжності;

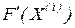– матриця Якобі, яка складається із елементів, що являють собою частинні похідні від усіх рівнянь системи по усім невідомим;

e – вектор-нев’язка, яка наближає вектор 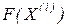до точки розв’язку системи; 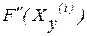– матриця Гессе, що складається із частинних похідних другого порядку. В двовимірному випадку маємо ці вектори на рисунку 26.

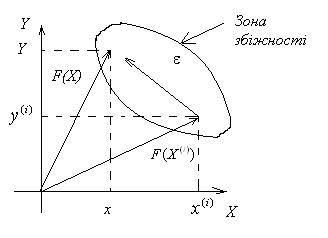
Рисунок 26 – Геометрична інтерпретація метода Ньютона

Враховуючи ітераційний процес, залишимо в ряду лише два перших елемента і одержимо значення вектора e:

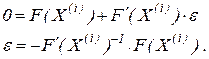
Звідси ітераційна формула буде мати вигляд:

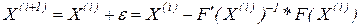або:

.

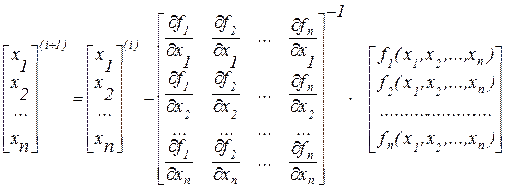Таким чином ітераційний процес по методу Ньютона реалізуються схемою: 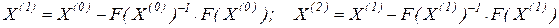і т.д.

Метод збігається до точки розв’язку дуже швидко (2-3 ітерації), але і для нього існує проблема вибору початкового вектора .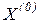

Застосуємо метод для попередньої задачі.

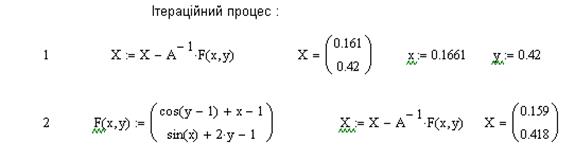
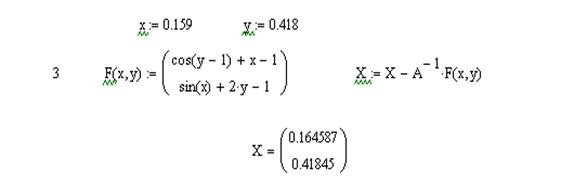
Перевіримо, розв’язок інструментарієм системи MathCad: