Преобразования Фурье и свертка

Пусть 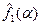и 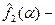преобразования Фурье абсолютно интегрируемых функций f₁(x) и f₂(x). Выясним, преобразованием Фурье какой функции является произведение :

.

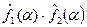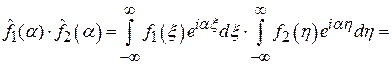
Двойной интеграл абсолютно сходится (существует повторный от модулей, поэтому существует двойной от модулей по следствию теоремы Фубини). Чтобы от двух экспонент перейти к одной, сделаем замену :

.

Перестановка интегралов законна в силу теоремы Фубини.

Определение. Сверткой функций f₁(x) и f₂(x) называется функция того же аргумента x 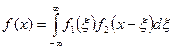. Свертка обозначается (f₁* f₂)(х).

При 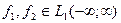свертка f(x)= (f₁* f₂)(х) существует при почти всех х и принадлежит 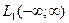в силу теоремы Фубини.

Итак, свертка двух функций из 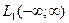преобразованием Фурье переводится в произведение их образов.

Свертка коммутативна и ассоциативна, поскольку преобразованием Фурье она переводится в коммутативную и ассоциативную операцию умножения.

Упражнение. Пусть е_а(х) – характеристическая функция интервала 0<x<a. Найти свёртку 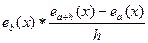, a<h<b.