Порядок выполнения работы. 1. Собрать модель исследуемой системы, параметры которой по вариантам приведены в таблице 6.1

1. Собрать модель исследуемой системы, параметры которой по вариантам приведены в таблице 6.1.

Таблица 6.1.

Номер варианта	k₁	k₂	Т₂	k₃	Т₃	d
		1.5	0.4		1.2	1.2
		0.8	0.2
			0.1		0.8	0.8
			0.3		1.5	1.5
	1.5		0.5		0.9	0.9
	2.5	1.5	0.2
		0.6	0.2		0.7	0.7
			0.5		0.6	0.6
	2.5	0.4	0.1		0.5	0.5
		0.3	0.6		1.4	2.2

2. . Подавая на вход единичное воздействие, зарисовать переходные процессы в системе при заданных параметрах. На экран графического монитора выводить входной, выходной сигналы.

3. Определить устойчивость замкнутой системы по критерию Гурвица. Для расчёта 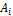Порядок выполнения работы. 1. Собрать модель исследуемой системы, параметры которой по вариантам приведены в таблице 6.1 - student2.ru можно использовать Меню → Анализ →Передаточные функции.

4. Проверить устойчивость разомкнутого контура САР по критерию Михайлова

Построить годограф характеристического полинома разомкнутой САР (годограф Михайлова) и по критерию Михайлова определить, устойчива ли разомкнутая САР. Сравнить результат с тем, что следует из вида переходной характеристики разомкнутой САР. Сделать выводы.

5. Оценить устойчивость замкнутой САР по критерию Найквиста

Построить годограф комплексного коэффициента передачи разомкнутого контура (годограф Найквиста). Используя критерий Найквиста, определить, будет ли устойчивой замкнутая САР. Определить запасы устойчивости САР по амплитуде и фазе. Сделать выводы. Сделать снимки экрана, сохранить проект.

6. Выполнить проверку устойчивости САР в разомкнутом и замкнутом состоянии, используя непосредственное вычисление полюсов характеристического полинома разомкнутой и замкнутой САР, проверить правильность вычислений, выполнив расчет "вручную".

7. Определить по ЛАЧХ и ЛФЧХ запасы устойчивости системы.

Контрольные вопросы

1. Как формулируется основное условие устойчивости линейных систем?

2. Каким образом коэффициент передачи разомкнутой системы влияет на вид годографа Михайлова?

3. Какой вид имеет переходная характеристика системы, находящейся на колебательной границе устойчивости?

4. Каковы условия положения системы на границе устойчивости по критериям Гурвица, Михайлова, Найквиста?

Основная литература

1. Пантелеев А. В., Теория управления в примерах и задачах: Учеб. пособие / А. В. Пантелеев, А. С. Бортаковский. — М.: Высш. шк., 2003.

Дополнительная литература

1. Бесекерский В.А., Попов Е. П. Теория систем автоматического управления. Учеб. пособие для вузов. – 4-е изд. – СПб: Профессия, 2004, 752 с.

2. Меньков А.В., Острейковский В.А. Теоретические основы автоматизированного управления.: Учеб. для вузов – М.: Оникс, 2005, 640 с.

3. Методы классической и современной теории автоматического управления в 5-ти т.: Учеб. для вузов / Под ред. К. А. Пупкова, Н. Д. Егупова – М.: Изд-во МГТУ им. Н.Э. Баумана.

4. Сборник задач по теории автоматического регулирования и управления/ Под ред. В.А. Бесекерского. – M.: Наука, 1978.

5. Зайцев Г.Ф. Теория автоматического управления и регулирования. 2-е изд., перераб. и доп. – К.: Высш. шк., 1989, 431 с.

6. Крутов В.И. Автоматическое управление и регулирование двигателей внутреннего сгорания. 5-е изд., перераб. и доп. – М.: Машиностроение, 1989, 416 с.

7. Основы теории автоматического регулирования. 2-е изд., перераб. и доп. / В. И. Крутов, Ф. М. Данилов, П.К. Кузьмик и др.; Под. ред. В.И. Крутова. – М.: Машиностроение, 1984, 368 с.