Быстрое преобразование Фурье
Классические формы прямого и обратного ДПФ хотя и просты и легко реализуемы на ЭВМ, однако их практическое применение ограничивается большим объемом вычислений, которые растут в квадратичной зависимости от объема выборки  .
.
Существуют различные способы сохранения объема вычислений спектра, которые приводят к так называемым алгоритма быстрого преобразования Фурье (БПФ). Алгоритмы БПФ основаны на устранении избыточности вычислений в классическом ДПФ. Эта избыточность просматривается в периодичности фазового множителя при которой
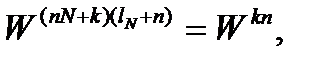 , в силу того, что
, в силу того, что 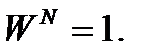
Не касаясь теоретических основ построения БПФ перейдем к изложению основных этапов преобразования, которые приводят к БПФ с прореживанием по времени.
Наиболее простая форма БПФ получается при  равному степени 2, т.е. когда
равному степени 2, т.е. когда  . Число
. Число 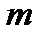 показывает количество ступеней преобразования.
показывает количество ступеней преобразования.
Этап 1. Входные отсчеты временной функции 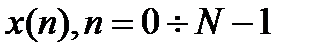 (при
(при 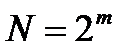 ) подвергается двоично-инверсной перестановке (ДИП). Идея ДИП состоит в следующем6двоичный код номера отсчета переставляется, формируя новый номер отсчета:
) подвергается двоично-инверсной перестановке (ДИП). Идея ДИП состоит в следующем6двоичный код номера отсчета переставляется, формируя новый номер отсчета:
Этап 2. Формируется дерево БПФ, способ построения которого для 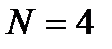 и
и 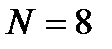 изображено на рис.4.1 и рис.4.2
изображено на рис.4.1 и рис.4.2

рис.4.1
рис.4.2
основу дерева БПФ составляют так называемая операция типа “бабочки”, которая отображена на рис.4.3, на нем же представлен алгоритм работы “бабочки”.
рис.4.3
Этап 3. Реализация операций “бабочки” последовательно по ступеням, начиная с “младшей”.
Мнемоническое правило расстановки весов ребер операций типа “бабочки” состоит в следующем: число показателей степени, начиная с нулевой фазового множителя последней ступени преобразования равно 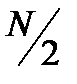 , где
, где  - объем выборки, например, для 8-точечного БПФ этим и множителями являются
- объем выборки, например, для 8-точечного БПФ этим и множителями являются 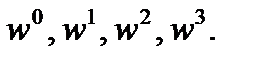
Для предшествующей ступени дерева ряд весовых коэффициентов прореживается за счет выбрасывания четных множителей. В результате такого прореживания остаются множители 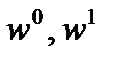 и наконец на первой ступени преобразования остается лишь один фазовый множитель
и наконец на первой ступени преобразования остается лишь один фазовый множитель 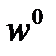 (рис.4.2)
(рис.4.2)
Для примера вычисли 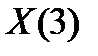 по дереву БПФ (рис.4.2)
по дереву БПФ (рис.4.2)
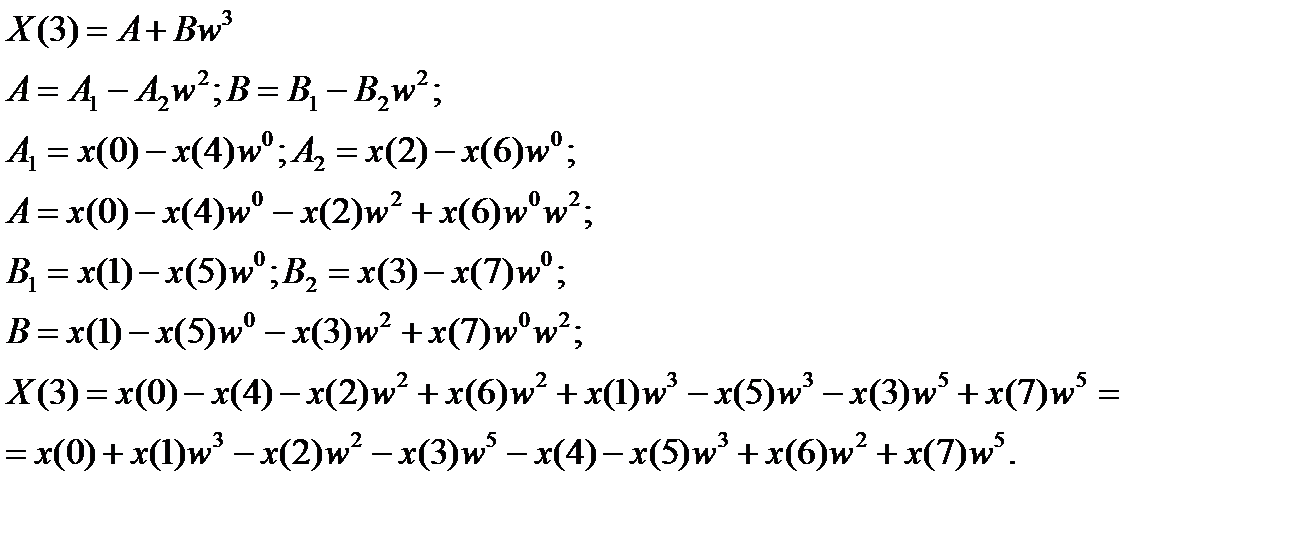
Рассчитаем 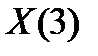 по алгоритму ДПФ
по алгоритму ДПФ
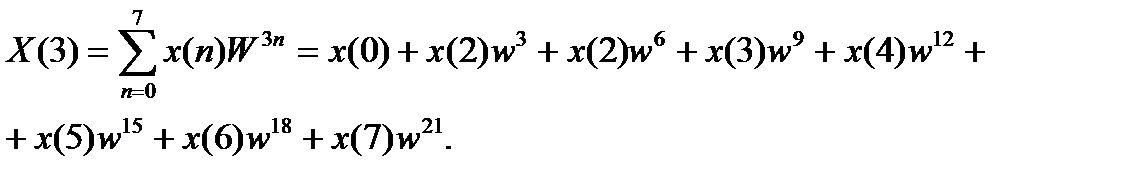
Эти выражения совпадают потому, что
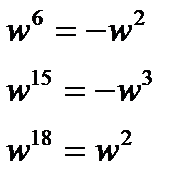
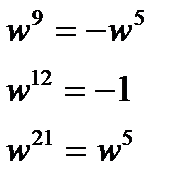
т.к. весовые коэффициенты периодические (рис.4.4)
рис.4.4
