Преобразование Фурье в классе

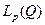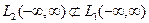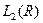В случае области бесконечной меры пространства не вкладываются одно в другое. В частности, (пример: ). Поэтому преобразование Фурье не применимо в обычном смысле к тем функциям из , которые не принадлежат 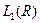. Тем не менее в пространстве 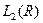можно ввести преобразование Фурье, но понимать его надо в более широком смысле, чем в .

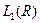Теорема (Планшерель, 1910 г.).Для всякой функции 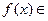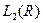интеграл

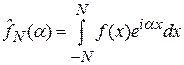(1)

представляет собой функцию, принадлежащую (по 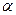) пространству . При 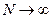последовательность 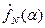в метрике имеет некоторый предел 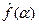, причем

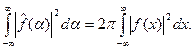(2)

Если f(x), кроме того, принадлежит 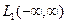, то 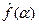есть обычное преобразование Фурье функции f(x). Поэтому 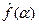и в общем случае (когда 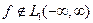) называется преобразованием Фурье от f(x).

Замечание 1.В теории обобщенных функций доказывается, что преобразование Фурье отображает 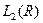на 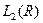взаимно однозначно и взаимно непрерывно.

Замечание 2.Справедливо более общее, чем (2), соотношение. Именно, есл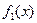и и 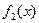– любые функции из 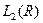, а 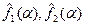– их преобразования Фурье, то

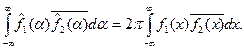
Для доказательства достаточно рассмотреть равенство (2) для .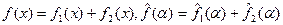

Соотношения между гладкостью функции и убыванием ее преобразования Фурье сохраняются и в .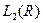

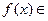
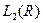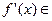
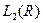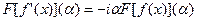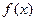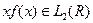Утверждение.Пусть является локально абсолютно непрерывной, и . Тогда . Верно и обратное утверждение: если и , то 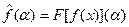есть локально абсолютно непрерывная функция, и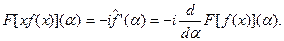

Доказательство в [2], стр.393-394.

Если 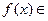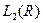и финитна (равна нулю вне отрезка [-b;b]), то она принадлежит пространству 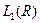и ее преобразование Фурье – функция 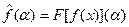может быть аналитически продолжена в плоскость 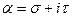. Действительно, выражение 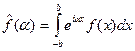определено при всех комплексных 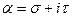. Оно удовлетворяет оценке 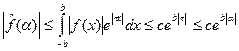и является аналитической функцией от .

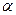Определение.Целая аналитическая функция 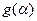, удовлетворяющая неравенству 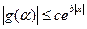, называется функцией экспоненциального типа .

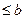Мы видим, что преобразование Фурье квадратично суммируемой функции, обращающейся в ноль при 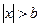, есть целая функция экспоненциального типа. Справедлива и обратная теорема.

Теорема (Винер - Палей) [2].Если целая функция 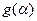экспоненциального типа 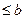интегрируема в квадрате по вещественной оси, то она является преобразованием Фурье функции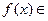 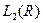, равной нулю вне отрезка [-b;b].